山东省济南市平阴县2022年中考一模数学试题
试卷更新日期:2022-07-13 类型:中考模拟
一、单选题
-
1. -9的绝对值是( )A、 B、 C、-9 D、92. 如图,粮仓可以近似地看作由圆锥和圆柱组成,其主视图是( )
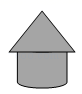 A、
A、 B、
B、 C、
C、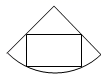 D、
D、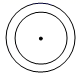 3. 《2020年国民经济和社会发展统计公报》显示,2020年我国共资助8990万人参加基本医疗保险,其中8990万用科学记数法表示为( )A、 B、 C、 D、4. 如图,已知a//b,一块含30°角的直角三角板,如图所示放置,∠2=30°,则∠1等于( )
3. 《2020年国民经济和社会发展统计公报》显示,2020年我国共资助8990万人参加基本医疗保险,其中8990万用科学记数法表示为( )A、 B、 C、 D、4. 如图,已知a//b,一块含30°角的直角三角板,如图所示放置,∠2=30°,则∠1等于( ) A、110° B、130° C、150° D、160°5. 下列四幅图案是四所大学校徽的主体标识,其中是中心对称图形的是( )A、
A、110° B、130° C、150° D、160°5. 下列四幅图案是四所大学校徽的主体标识,其中是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 6. 如图,已知数轴上 两点表示的数分别是 ,则计算 正确的是( )
6. 如图,已知数轴上 两点表示的数分别是 ,则计算 正确的是( )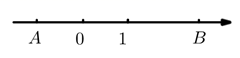 A、 B、 C、 D、7. 计算 的结果是( )A、 B、 C、1 D、-18. 在六张卡片上分别写有6, ,3.1415, ,0, 六个数,从中随机抽取一张,卡片上的数为无理数的概率是( )A、 B、 C、 D、9. 在同一直角坐标系中,反比例函数 与一次函数 的图象可能是( )A、
A、 B、 C、 D、7. 计算 的结果是( )A、 B、 C、1 D、-18. 在六张卡片上分别写有6, ,3.1415, ,0, 六个数,从中随机抽取一张,卡片上的数为无理数的概率是( )A、 B、 C、 D、9. 在同一直角坐标系中,反比例函数 与一次函数 的图象可能是( )A、 B、
B、 C、
C、 D、
D、 10. 如图,在 中, ,按以下步骤作图:①以 为圆心,任意长为半径作弧,分别交 、 于 、 两点;②分别以 、 为圆心,以大于 的长为半径作弧,两弧相交于点 ;③作射线 ,交边 于 点.若 , ,则线段 的长为( )
10. 如图,在 中, ,按以下步骤作图:①以 为圆心,任意长为半径作弧,分别交 、 于 、 两点;②分别以 、 为圆心,以大于 的长为半径作弧,两弧相交于点 ;③作射线 ,交边 于 点.若 , ,则线段 的长为( ) A、3 B、 C、 D、11. 如图,为了测量某建筑物BC的高度,小颖采用了如下的方法:先从与建筑物底端B在同一水平线上的A点出发,沿斜坡AD行走130米至坡顶D处,再从D处沿水平方向继续前行若干米后至点E处,在E点测得该建筑物顶端C的仰角为60°,建筑物底端B的俯角为45°,点A、B、C、D、E在同一平面内,斜坡AD的坡度 . 根据小颖的测量数据,计算出建筑物BC的高度约为( )(参考数据:)
A、3 B、 C、 D、11. 如图,为了测量某建筑物BC的高度,小颖采用了如下的方法:先从与建筑物底端B在同一水平线上的A点出发,沿斜坡AD行走130米至坡顶D处,再从D处沿水平方向继续前行若干米后至点E处,在E点测得该建筑物顶端C的仰角为60°,建筑物底端B的俯角为45°,点A、B、C、D、E在同一平面内,斜坡AD的坡度 . 根据小颖的测量数据,计算出建筑物BC的高度约为( )(参考数据:)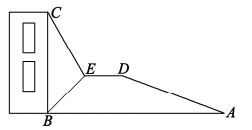 A、136.6米 B、86.7米 C、186.7米 D、86.6米12. 二次函数(、、是常数,且)的自变量与函数值的部分对应值如下表:
A、136.6米 B、86.7米 C、186.7米 D、86.6米12. 二次函数(、、是常数,且)的自变量与函数值的部分对应值如下表:…
-1
0
1
2
…
…
2
2
…
且当时,对应的函数值 . 有以下结论:①;②;③关于的方程的负实数根在和0之间;④和在该二次函数的图象上,则当实数时, . 其中正确的结论是( )
A、①② B、②③ C、③④ D、②③④二、填空题
-
13. 因式分解: .14. 如图所示的六边形广场由若干个大小完全相同的黑色和白色正三角形组成,一只小鸟在广场上随机停留,刚好落在黑色三角形区域的概率为 .
 15. 如图,在正五边形ABCDE中,AC与BE相交于点F,则∠AFE的度数为 .
15. 如图,在正五边形ABCDE中,AC与BE相交于点F,则∠AFE的度数为 .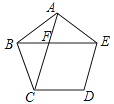 16. 若关于 的一元二次方程 的一个解是 ,则 的值是 .17. 如图,正方形内接于 , , 分别与相切于点和点 , 的延长线与的延长线交于点 . 已知 , 则图中阴影部分的面积为 .
16. 若关于 的一元二次方程 的一个解是 ,则 的值是 .17. 如图,正方形内接于 , , 分别与相切于点和点 , 的延长线与的延长线交于点 . 已知 , 则图中阴影部分的面积为 .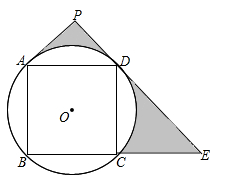 18. 如图,正方形OABC的边长为2,将正方形OABC绕点O逆时针旋转角α(0°<α<180°)得到正方形OA′B′C′,连接BC′,当点A′恰好落在线段BC′上时,线段BC′的长度是 .
18. 如图,正方形OABC的边长为2,将正方形OABC绕点O逆时针旋转角α(0°<α<180°)得到正方形OA′B′C′,连接BC′,当点A′恰好落在线段BC′上时,线段BC′的长度是 .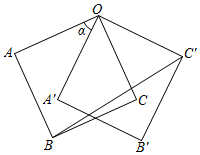
三、解答题
-
19. 计算:tan45°20. 解不等式组: ,并写出所有整数解.21. 如图,在平行四边形ABCD中,E、F为对角线BD上的
两点,且∠BAE=∠DCF.
求证:BE=DF.
 22. 为了解中考体育科目训练情况,从全县九年级学生中随机抽取了部分学生进行了一次中考体育科目测试(把测试结果分为四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格),并将测试结果绘成了如下两幅不完整的统计图.请根据统计图中的信息解答下列问题:
22. 为了解中考体育科目训练情况,从全县九年级学生中随机抽取了部分学生进行了一次中考体育科目测试(把测试结果分为四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格),并将测试结果绘成了如下两幅不完整的统计图.请根据统计图中的信息解答下列问题: (1)、本次抽样测试的学生人数是;(2)、图中∠α的度数是 ▲ , 并把条形统计图补充完整;(3)、该县九年级有学生3000名,如果全部参加这次中考体育科目测试,请估计不及格的人数为 .(4)、测试老师想从4位同学(分别记为E、F、G、H,其中E为小明)中随机选择两位同学了解平时训练情况,请用列表或画树形图的方法求出选中小明的概率.23. 如图,在Rt△AOB中,∠AOB=90°,⊙O与AB相交于点C,与AO相交于点E,连接CE,已知∠AOC=2∠ACE.
(1)、本次抽样测试的学生人数是;(2)、图中∠α的度数是 ▲ , 并把条形统计图补充完整;(3)、该县九年级有学生3000名,如果全部参加这次中考体育科目测试,请估计不及格的人数为 .(4)、测试老师想从4位同学(分别记为E、F、G、H,其中E为小明)中随机选择两位同学了解平时训练情况,请用列表或画树形图的方法求出选中小明的概率.23. 如图,在Rt△AOB中,∠AOB=90°,⊙O与AB相交于点C,与AO相交于点E,连接CE,已知∠AOC=2∠ACE. (1)、求证:AB为⊙O的切线;(2)、若AO=20,BO=15,求AE的长.24. 2020年我国新型冠状病毒肺炎疫情防控工作进入常态化,某社区为检测出入小区人员体温情况,特采购了一批测温枪,已知1支A型号测温枪和2支B型号测温枪共需380元,2支A型号测温枪和3支B型号测温枪共需610元.(1)、两种型号的测温枪的单价各是多少元?(2)、已知该社区需要采购两种型号的测温枪共40支,且A型号的数量不超过B型号的数量的3倍,请设计出最省钱的购买方案,并说明理由.25. 如图,在平面直角坐标系 中,一次函数 的图象与反比例函数 的图象相交于点 ,与x轴相交于点B.
(1)、求证:AB为⊙O的切线;(2)、若AO=20,BO=15,求AE的长.24. 2020年我国新型冠状病毒肺炎疫情防控工作进入常态化,某社区为检测出入小区人员体温情况,特采购了一批测温枪,已知1支A型号测温枪和2支B型号测温枪共需380元,2支A型号测温枪和3支B型号测温枪共需610元.(1)、两种型号的测温枪的单价各是多少元?(2)、已知该社区需要采购两种型号的测温枪共40支,且A型号的数量不超过B型号的数量的3倍,请设计出最省钱的购买方案,并说明理由.25. 如图,在平面直角坐标系 中,一次函数 的图象与反比例函数 的图象相交于点 ,与x轴相交于点B.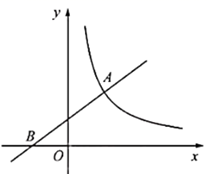 (1)、求反比例函数的表达式;(2)、过点A的直线交反比例函数的图象于另一点C,交x轴正半轴于点D,当 是以 为底的等腰三角形时,求直线 的函数表达式及点C的坐标.26. 在等腰△ABC中,AB=AC,点D是BC边上一点(不与点B、C重合),连结AD.
(1)、求反比例函数的表达式;(2)、过点A的直线交反比例函数的图象于另一点C,交x轴正半轴于点D,当 是以 为底的等腰三角形时,求直线 的函数表达式及点C的坐标.26. 在等腰△ABC中,AB=AC,点D是BC边上一点(不与点B、C重合),连结AD. (1)、如图1,若∠C=60°,点D关于直线AB的对称点为点E,连结AE,DE,则∠BDE=;(2)、如图2,若∠C=60°,将线段AD绕点A顺时针旋转60°得到线段AE,连结BE.探究CD与BE的数量关系,并证明;(3)、如图3,若=k,且∠ADE=∠C.试探究BE、BD、AC之间满足的数量关系,并证明.27. 如图,抛物线 经过点 , ,与y轴正半轴交于点C , 且 .抛物线的顶点为D , 对称轴交x轴于点E.直线 经过B , C两点.
(1)、如图1,若∠C=60°,点D关于直线AB的对称点为点E,连结AE,DE,则∠BDE=;(2)、如图2,若∠C=60°,将线段AD绕点A顺时针旋转60°得到线段AE,连结BE.探究CD与BE的数量关系,并证明;(3)、如图3,若=k,且∠ADE=∠C.试探究BE、BD、AC之间满足的数量关系,并证明.27. 如图,抛物线 经过点 , ,与y轴正半轴交于点C , 且 .抛物线的顶点为D , 对称轴交x轴于点E.直线 经过B , C两点.
 (1)、求抛物线及直线 的函数表达式;(2)、点F是抛物线对称轴上一点,当 的值最小时,求出点F的坐标及 的最小值;(3)、连接 ,若点P是抛物线上对称轴右侧一点,点Q是直线 上一点,试探究是否存在以点E为直角顶点的 ,且满足 .若存在,求出点P的坐标;若不存在,请说明理由.
(1)、求抛物线及直线 的函数表达式;(2)、点F是抛物线对称轴上一点,当 的值最小时,求出点F的坐标及 的最小值;(3)、连接 ,若点P是抛物线上对称轴右侧一点,点Q是直线 上一点,试探究是否存在以点E为直角顶点的 ,且满足 .若存在,求出点P的坐标;若不存在,请说明理由.