山东省烟台市莱山区2021-2022学年九年级下学期期中数学试题
试卷更新日期:2022-07-13 类型:期中考试
一、单选题
-
1. 下列垃圾分类图标分别表示:“可回收垃圾”、“有害垃圾”、“厨余垃圾”、“其它垃圾”,其中既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 2021年5月11日,第七次全国人口普查结果公布,我国总人口大约为1412000000人,数字1412000000用科学记数法表示为( )A、 B、 C、 D、3. 如图,该几何体的主视图是( )
2. 2021年5月11日,第七次全国人口普查结果公布,我国总人口大约为1412000000人,数字1412000000用科学记数法表示为( )A、 B、 C、 D、3. 如图,该几何体的主视图是( )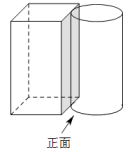 A、
A、 B、
B、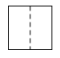 C、
C、 D、
D、 4. 如图,小球从A入口往下落,在每个交叉口都有向左或向右两种可能,且可能性相等,则小球从E出口落出的概率是( )
4. 如图,小球从A入口往下落,在每个交叉口都有向左或向右两种可能,且可能性相等,则小球从E出口落出的概率是( )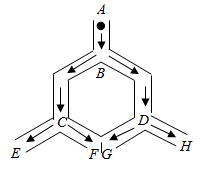 A、 B、 C、 D、5. 用计算器求值时,需相继按“3”,“”,“5”,“=”键,若小明相继按“”,“9”,“”,“(-)”,“3”,“=”键,则输出结果是( )A、-9 B、-27 C、27 D、6. 定义新运算 , 对于任意实数a,b满足 . 例如 , 若是关于x的方程,则它的根的情况是( )A、有一个实根 B、没有实数根 C、有两个相等的实数根 D、有两个不相等的实数根7. 如图,正六边形ABCDEF的边长为6,以顶点A为圆心,AB的长为半径画圆,用图中阴影部分围成一个圆锥的侧面(接缝忽略不计),则该圆锥的高为( )
A、 B、 C、 D、5. 用计算器求值时,需相继按“3”,“”,“5”,“=”键,若小明相继按“”,“9”,“”,“(-)”,“3”,“=”键,则输出结果是( )A、-9 B、-27 C、27 D、6. 定义新运算 , 对于任意实数a,b满足 . 例如 , 若是关于x的方程,则它的根的情况是( )A、有一个实根 B、没有实数根 C、有两个相等的实数根 D、有两个不相等的实数根7. 如图,正六边形ABCDEF的边长为6,以顶点A为圆心,AB的长为半径画圆,用图中阴影部分围成一个圆锥的侧面(接缝忽略不计),则该圆锥的高为( ) A、4 B、 C、 D、8. 如图,在菱形ABCD中,AB=2,∠A=120°,过菱形ABCD的对称中心O分别作边AB,BC的垂线,交各边于点E,F,G,H.则四边形EFGH的周长为( )
A、4 B、 C、 D、8. 如图,在菱形ABCD中,AB=2,∠A=120°,过菱形ABCD的对称中心O分别作边AB,BC的垂线,交各边于点E,F,G,H.则四边形EFGH的周长为( )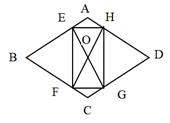 A、 B、 C、 D、9. 如图,在平面直角坐标系中,等腰直角三角形OAB, , 点O为坐标原点,点B在x轴上,点A的坐标是 . 若将△OAB绕点O顺时针方向依次旋转45°后得到 , , , …,可得 , , …,则的坐标是( )
A、 B、 C、 D、9. 如图,在平面直角坐标系中,等腰直角三角形OAB, , 点O为坐标原点,点B在x轴上,点A的坐标是 . 若将△OAB绕点O顺时针方向依次旋转45°后得到 , , , …,可得 , , …,则的坐标是( )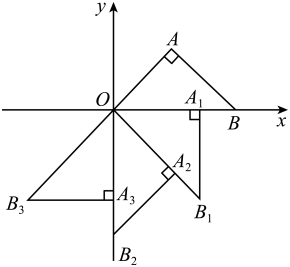 A、 B、 C、 D、10. 一次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线x=1.下列结论:①abc>0;②若(−3,y1),(4,y2)在抛物线上,则y1<y2;③当−1<x<3时,y<0时;④8a+c>0.其中正确的有( )
A、 B、 C、 D、10. 一次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线x=1.下列结论:①abc>0;②若(−3,y1),(4,y2)在抛物线上,则y1<y2;③当−1<x<3时,y<0时;④8a+c>0.其中正确的有( )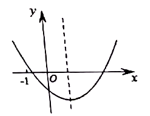 A、①② B、①④ C、①③④ D、②④
A、①② B、①④ C、①③④ D、②④二、填空题
-
11. 在函数y= + 中,自变量x的取值范围是 .12. 2022年中考模拟体育测试中,我区某校随机抽取了10名男生的引体向上成绩,将这组数据整理后制成如下统计表,下列说法中正确的是 . (填序号)
①这组数据的众数是8;
②这组数据的中位数是7;
③这组数据的平均数是7;
④这组数据的方差是2.2
成绩(次)
9
8
6
5
人数(名)
2
3
3
2
13. 下图是可调躺椅示意图,AE与BD交于点C.小明觉得当躺椅的角度是如图所示的数据时最舒适,此时度. 14. 七巧板是我们祖先的一项创造,被誉为“东方魔板”,小明用边长为的正方形分割制作的七巧板拼摆成的“叶问蹬”图.则图中抬起的“腿”(即阴影部分)的面积为 .
14. 七巧板是我们祖先的一项创造,被誉为“东方魔板”,小明用边长为的正方形分割制作的七巧板拼摆成的“叶问蹬”图.则图中抬起的“腿”(即阴影部分)的面积为 .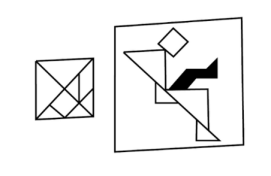 15. 如图,正方形网格中,点A,O,B,E均在格点上.⊙O过点A,E且与AB交于点C,点D是⊙O上一点,则 .
15. 如图,正方形网格中,点A,O,B,E均在格点上.⊙O过点A,E且与AB交于点C,点D是⊙O上一点,则 . 16. 如图,抛物线与x轴交于A,B两点,点C的坐标为 , ⊙C半径为4,P是⊙C上一动点,Q是线段PB的中点,连接OQ.则线段OQ的最大值是 .
16. 如图,抛物线与x轴交于A,B两点,点C的坐标为 , ⊙C半径为4,P是⊙C上一动点,Q是线段PB的中点,连接OQ.则线段OQ的最大值是 .
三、解答题
-
17. 先化简再求值:
,其中x是不等式组 的一个整数解.
18. 自疫情暴发以来,我国科研团队经过不懈努力,成功地研发出了多种新冠疫苗,以下是某地甲、乙两家医院5月份某天各年龄段接种疫苗人数的频数分布表和接种总人数的形统计图: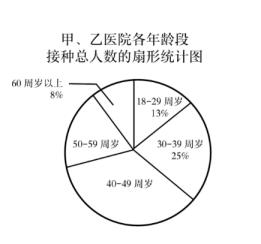
甲医院
乙医院
年龄段
频数
频率
频数
频率
18—29周岁
900
0.15
400
0.1
30—39周岁
a
0.25
1000
0.25
40—49周岁
2100
b
c
0.225
50—59周岁
1200
0.2
1200
0.3
60周岁以上
300
0.05
500
0.125
(1)、根据上面图表信息,回答下列问题:①填空:a= , b= , c=;
②在甲、乙两医院当天接种疫苗的所有人员中,40—49周岁年龄段人数在扇形统计图中所占圆心角为;
(2)、若A,B,C三人都于当天随机到这两家医院接种疫苗,请用列表或画树状图的方法求这三人在同一家医院接种的概率.19. 在《阿基米德全集》中的《引理集》中记录了古希腊数学家阿基米德提出的有关圆的一个引理.如图,已知 是弦 上一点,请你根据以下步骤完成这个引理的作图过程. (1)、尺规作图(保留作图痕迹,不写作法):
(1)、尺规作图(保留作图痕迹,不写作法):①作线段 的垂直平分线 ,分别交 于点 于点 ,连接 ;
②以点 为圆心, 长为半径作弧,交 于点 ( 两点不重合),连接 .
(2)、直接写出引理的结论:线段 的数量关系.20. 如图,以原点O为顶点作正方形OABC,已知点 , 点A在x轴的正半轴上,直线与边AB,OA分别交于点D,M.反比例函数的图象过点D,与BC交于点N,连接MN.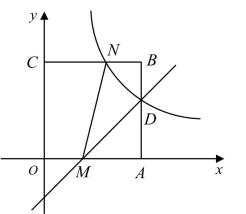 (1)、求反比例函数的表达式;(2)、若点P是直线DM上的动点,当时,求点P的坐标.21. 为响应国家东西部协作战略,烟台对口协作重庆巫山,采购巫山恋橙助力乡村振兴.巫山恋橙主要有纽荷尔和默科特两个品种,已知1箱纽荷尔价格比1箱默科特少20元,300元购买纽荷尔的箱数与400元购买默科特的箱数相同.(1)、纽荷尔和默科特每箱分别是多少元?(2)、我市动员市民采购两种巫山恋橙,据统计,市民响应积极,预计共购买两种隥子150箱,且购买纽荷尔的数量不少于默科特的2倍,请你求出购买总费用的最大值.22. 一酒精消毒瓶如图1,为喷嘴,为按压柄,为伸缩连杆,和为导管,其示意图如图2, , , . 当按压柄按压到底时,转动到 , 此时(如图3).
(1)、求反比例函数的表达式;(2)、若点P是直线DM上的动点,当时,求点P的坐标.21. 为响应国家东西部协作战略,烟台对口协作重庆巫山,采购巫山恋橙助力乡村振兴.巫山恋橙主要有纽荷尔和默科特两个品种,已知1箱纽荷尔价格比1箱默科特少20元,300元购买纽荷尔的箱数与400元购买默科特的箱数相同.(1)、纽荷尔和默科特每箱分别是多少元?(2)、我市动员市民采购两种巫山恋橙,据统计,市民响应积极,预计共购买两种隥子150箱,且购买纽荷尔的数量不少于默科特的2倍,请你求出购买总费用的最大值.22. 一酒精消毒瓶如图1,为喷嘴,为按压柄,为伸缩连杆,和为导管,其示意图如图2, , , . 当按压柄按压到底时,转动到 , 此时(如图3).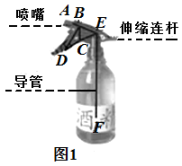
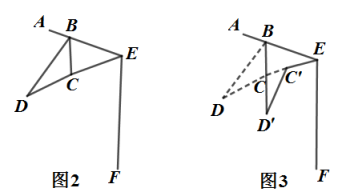
(参考数据: , , , , , )
(1)、求点转动到点的路径长;(2)、求点到直线的距离(结果精确到).23. 如图,AB是⊙O的弦,点C是的中点,连接BC,过点A作交⊙O于点D.连接CD,延长DA至E,连接CE,使 .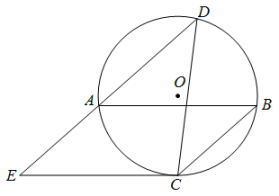 (1)、求证:CE是⊙O的切线;(2)、若 , , 求AD的长.24. 问题背景:
(1)、求证:CE是⊙O的切线;(2)、若 , , 求AD的长.24. 问题背景:如图,已知△ABC中, , , , 点P为平面内不与点A,C重合的任意一点,连接CP,将线段CP绕点P顺时针旋转 , 得线段PD,连接CD,AP.点E,F分别为BC,CD的中点,设直线AP与直线EF相交所成的较小角为 , 探究的值AB和的度数.
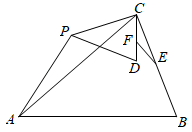 (1)、【问题发现】如图1,时, , ;
(1)、【问题发现】如图1,时, , ;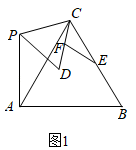 (2)、如图2,时, , .
(2)、如图2,时, , . (3)、【类比探究】如图3,时,请探究出的值和的度数并证明;
(3)、【类比探究】如图3,时,请探究出的值和的度数并证明;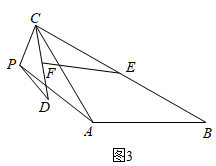 (4)、【拓展延伸】通过以上的探究请直接写出你发现的规律:(用含m、n的式子表示);(用含的式子表示).25. 如图,平面直角坐标系中,正方形ABCD的顶点A,B在x轴上,抛物线经过A,两点,且与直线DC交于另一点E.
(4)、【拓展延伸】通过以上的探究请直接写出你发现的规律:(用含m、n的式子表示);(用含的式子表示).25. 如图,平面直角坐标系中,正方形ABCD的顶点A,B在x轴上,抛物线经过A,两点,且与直线DC交于另一点E.
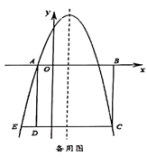 (1)、求抛物线的解析式:(2)、P为y轴上一点,过点P作抛物线对称轴的垂线,垂足为Q,连接EQ,AP.试求的最小值;(3)、N为平面内一点,在抛物线对称轴上是否存在点M,使得以点M,N,E,A为顶点的四边形是菱形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式:(2)、P为y轴上一点,过点P作抛物线对称轴的垂线,垂足为Q,连接EQ,AP.试求的最小值;(3)、N为平面内一点,在抛物线对称轴上是否存在点M,使得以点M,N,E,A为顶点的四边形是菱形?若存在,请直接写出点M的坐标;若不存在,请说明理由.