云南省昆明市呈贡区2022年中考数学模拟试题

试卷更新日期：2022-07-13 类型：中考模拟

进入出卷网下载

一、单选题

1. 在党中央的坚强领导下，经过艰苦卓绝的奋战，新冠疫情得到了有效控制．研究发现，某种新型冠状病毒的直径约为130纳米，已知130纳米＝0.00000013米，0.00000013用科学记数法表示是（）

A、 $0.13 \times 1 0^{- 6}$ B、 $0.13 \times 1 0^{- 7}$ C、 $1.3 \times 1 0^{- 6}$ D、 $1.3 \times 1 0^{- 7}$

查看试题解析
2. 下列计算正确的是（）

A、 $2 a^{3} + a^{3} = 3 a^{6}$ B、 ${(a^{2})}^{3} = a^{6}$ C、 ${(- 3 a^{3} b)}^{2} = 6 a^{6} b^{2}$ D、 ${(a - b)}^{2} = a^{2} - b^{2}$

查看试题解析
3. 如图所示的几何体的左视图是（）

A、 B、 C、 D、

查看试题解析
4. 下列判断错误的是（）

A、了解一批冰箱的使用寿命，采用抽样调查的方式 B、一组数据2，5，3，5，6，8的众数和中位数都是5 C、甲、乙两组队员身高数据的方差分别为 ${S_{甲}}^{2} = 0.2$ ， ${S_{乙}}^{2} = 0.1$ ，那么甲组队员的身高比较整齐 D、一个不透明的袋子里装有红球、蓝球共20个，这些球除颜色外都相同，小红通过多次试验发现，摸出红球的频率稳定在0.25左右，则袋子中红球的个数可能是5个

查看试题解析
5. 如图，AB//CD，DB⊥BC，垂足为点B，∠1＝40°，则∠2的度数是（）

A、60° B、50° C、40° D、30°

查看试题解析
6. 一元二次方程 $3 x^{2} + 2 x - 1 = 0$ 的根的情况是（）

A、没有实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、无法判断

查看试题解析
7. 按一定规律排列的单项式： $a^{2}$ ， $- 4 a^{3}$ ， $9 a^{4}$ ， $- 16 a^{5}$ ， $25 a^{6}$ ， ……，第n个单项式是（）

A、 ${(- 1)}^{n + 1} n^{2} a^{n + 1}$ B、 ${(- 1)}^{n} n^{2} a^{n + 1}$ C、 ${(- 1)}^{n + 1} n^{2} a^{n}$ D、 ${(- 1)}^{n} n^{2} a^{n}$

查看试题解析
8. 如图，已知等腰△ABC的周长为18，底边BC＝4．尺规作图如下：分别以点A，C为圆心，大于 $\frac{1}{2} A C$ 的长为半径作弧，连接两弧交点的直线交AB边于点D，则△BCD的周长为（）

A、11 B、12 C、13 D、14

查看试题解析
9. 如图，⊙O是△ABC的外接圆，AD是⊙O的直径．若 $A D = 13$ ，弦 $A B = 5$ ，则 $t a n ∠ A C B$ 的值为（）

A、 $\frac{13}{5}$ B、 $\frac{12}{13}$ C、 $\frac{5}{13}$ D、 $\frac{5}{12}$

查看试题解析
10. 如图，从一个边长为2m的正六边形ABCDEF铁皮上剪出一个扇形CAE，如果将剪下来的扇形围成一个圆锥，则该圆锥的底面圆的半径为（）

A、 $\frac{\sqrt{3}}{2} m$ B、 $\frac{\sqrt{3}}{3} m$ C、 $\frac{\sqrt{3}}{4} m$ D、 $\sqrt{3} m$

查看试题解析
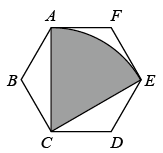11. 若关于x的分式方程 $\frac{x - 3 m}{x - 2} - 1 = \frac{3 m}{x + 2}$ 的解是负数，则m的取值范围为（）

A、 $m < \frac{1}{3}$ 且 $m \neq 0$ B、 $m < \frac{1}{3}$ C、 $m > - \frac{1}{3}$ 且 $m \neq 0$ D、 $m > - \frac{1}{3}$

查看试题解析
12. 如图，在平面直角坐标系中，反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象同时经过等腰Rt△OAB的顶点A，B，且∠OAB＝90°，若点A的横坐标为2，则k的值为（）

A、 $2 + \sqrt{5}$ B、 $4 + \sqrt{5}$ C、 $4 + 2 \sqrt{5}$ D、 $2 + 2 \sqrt{5}$

查看试题解析

二、填空题

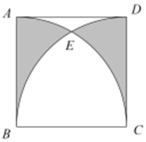
13. 2022的相反数为.

查看试题解析
14. 计算： ${(π - 3)}^{0} + {(\frac{1}{3})}^{- 2} - \sqrt{9} =$ ．

查看试题解析
15. 若 $m = 2 n \neq 0$ ，则 $\frac{m^{2} - n^{2}}{m n - m^{2}}$ 的值为．

查看试题解析
16. 一个多边形的内角和是它的外角和的5倍，则这个多边形的边数为。

查看试题解析
17. 如图，在正方形ABCD中，以点B，C为圆心，BC为半径作 $\overset{⌢}{A C}$ ， $\overset{⌢}{B D}$ ，两弧相交于点E，若AB＝2，则阴影部分的面积为．

查看试题解析
18. 在菱形ABCD中，AB＝4，∠ABC＝60°，连接AC，BD，E是菱形边上或对角线上一点，且∠CAE＝30°，则BE的长为．

查看试题解析

三、解答题

19. 2021年7月24日，教育部官网正式发布由中共中央办公厅、国务院办公厅印发的《关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见》．某市就“学生完成书面作业需要的时间问题”随机调查了辖区内部分初中学生．将收集的信息进行统计分成A，B，C，D四个组别，其中A：30分钟以下；B：30~60分钟；C：60~90分钟；D：90分钟以上．并将调查结果绘制成两幅不完整的统计图表：
组别
学生完成书面作业需要时间t（分钟）
人数
A
$0 < t \leq 30$
60
B
$30 < t \leq 60$
m
C
$60 < t \leq 90$
160
D
$t > 90$
80
请根据上述信息解答下列问题：

(1)、表格中的m＝；

(2)、C组对应扇形的圆心角为度；本次调查数据的中位数落在组内；

(3)、若该市辖区约有78000名初中学生，请你估计能在国家规定的90分钟（含90分钟）内完成书面作业的学生人数？

查看试题解析
20. 2022年3月23日“天宫课堂”第二课在中国空间站正式开讲了，“太空教师”翟志刚、王亚平、叶光富又上了一堂精彩的太空科普课．某学校为了培养学生对航天知识的学习兴趣，将举办航天知识讲座．现决定从A，B，C，D四名志愿者中随机选取两名志愿者担任引导员．

(1)、“B志愿者被选中”是事件（填“随机”或“不可能”或“必然”）；

(2)、请用列表或画树状图的方法求出抽到A，B两名志愿者的概率．

查看试题解析
21. “冰墩墩”和“雪容融”分别是北京2022年冬季奥运会和冬残奥运会的吉祥物．该吉祥物深受全世界人民的喜爱，某生产厂家经授权每天生产两种吉祥物挂件共600件，且当天全部售出，生产成本和销售单价如下表所示：

生产成本（元/件）
销售单价（元/件）
“冰墩墩”
42
50
“雪容融”
35
41
设该厂每天制作“冰墩墩”挂件x件，每天获得的利润为y元．

(1)、求出y与x之间的函数关系式；

(2)、若该厂每天投入总成本不超过23800元，应怎样安排“冰墩墩”和“雪容融”的制作量，可使该厂一天所获得的利润最大，请求出最大利润和此时两个挂件的制作数量．

查看试题解析
22. 如图，BC是⊙O的直径，BD平分∠ABC交⊙O于点D，DA⊥BA于点A，AB交⊙O于点E．

(1)、求证：AD是⊙O的切线；

(2)、若AD＝6，AE＝3，求 $s i n ∠ A B C$ 的值．

查看试题解析
23. 如图，在矩形ABCD中，E为BC的中点，AE⊥BD于点F，连接CF．

(1)、求证：AB＝CF；

(2)、若 $A B = 4 \sqrt{2}$ ，求DF的长．

查看试题解析
24. 在平面直角坐标系xOy中，已知抛物线 $y = a x^{2} + b x + c$ 交x轴于 $A (- 1 ， 0)$ ， $B (4 ， 0)$ 两点，与y轴交于点 $C (0 ， 3)$ ．

(1)、求抛物线的函数解析式；

(2)、如图1，点D为直线BC上方抛物线上一动点，连接AD，交BC于点E，求 $\frac{D E}{A E}$ 的最大值；

(3)、如图2，点P为抛物线上一动点，是否存在点P，使得2∠PCB＝∠OCB，若存在，请直接写出点P的坐标；若不存在，请说明理由．

查看试题解析

组别	学生完成书面作业需要时间t（分钟）	人数
A	$0 < t \leq 30$	60
B	$30 < t \leq 60$	m
C	$60 < t \leq 90$	160
D	$t > 90$	80

	生产成本（元/件）	销售单价（元/件）
“冰墩墩”	42	50
“雪容融”	35	41