云南省大理州2022年初中学业水平模拟考试数学试题

试卷更新日期：2022-07-13 类型：中考模拟

进入出卷网下载

一、单选题

1. 下面四个几何体中，主视图是三角形的几何体共有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 截至2022年3月1日新学期开学之际，全国累计报告接种新冠病毒疫苗约314000万剂次．将314000万用科学记数法表示为（）万．

A、 $31.4 \times 1 0^{4}$ B、 $3.14 \times 1 0^{5}$ C、 $0.314 \times 1 0^{6}$ D、 $3.14 \times 1 0^{- 5}$

查看试题解析
3. 下列运算正确的是（）

A、 $a^{3} \cdot a^{2} = a^{6}$ B、 $2 a (3 a - 1) = 6 a^{2} - 1$ C、 $a^{8} \div a^{4} = x^{2}$ D、 ${(2 a)}^{3} = 8 a^{3}$

查看试题解析
4. 如图， $A P_{1}$ 为 $△ A B C$ 的中线， $A P_{2}$ 为 $△ A P_{1} C$ 的中线， $A P_{3}$ 为 $△ A P_{2} C$ 的中线……按此规律， $A P_{n}$ 为 $△ A P_{n - 1} C$ 的中线．若 $△ A B C$ 的面积为S，则 $△ A P_{n} C$ 的面积为（）

A、 $\frac{S}{2^{n - 2}}$ B、 $\frac{S}{2^{n - 1}}$ C、 $\frac{S}{2^{n}}$ D、 $\frac{S}{2^{n + 1}}$

查看试题解析
5. 在课外活动中，有10名同学进行了投篮比赛，限每人投10次，投中次数与人数如下表：

投中次数

5

7

8

9

10

人数

2

3

3

1

1

则这10人投中次数的平均数和中位数分别是（）

A、 $3.9 ， 7$ B、 $6.4 ， 7.5$ C、 $7.4 ， 8$ D、 $7.4 ， 7.5$

查看试题解析
6. 如图，等边 $△ A B C$ 的边长为 $2$ ， $D E$ 是它的中位线，则下列三个结论：① $D E = 1$ ；② $△ C D E ∽ △ C A B$ ；③ $△ C D E$ 与 $△ C A B$ 的面积之比为 $1 ： 4$ ．其中正确的有（）

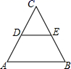A、0个 B、1个 C、2个 D、3个

查看试题解析
7. 若关于x的一元二次方程 $x^{2} - 2 x + m = 0$ 有两个不相等的实数根，则m的取值范围是（）

A、 $m \leq 1$ B、 $m < 1$ C、 $m > 1$ D、 $m \geq 1$

查看试题解析
8. 一个多边形的内角和是外角和的2倍，这个多边形的边数为（　　）

A、5 B、6 C、7 D、8

查看试题解析
9. 计算： $| - 2 | + 3 s i n 30 ° - 2^{- 1} - (2022 - π)^{0}$ 等于（）

A、-2 B、 $- \frac{1}{2}$ C、2 D、0

查看试题解析
10. 在“扶贫攻坚”活动中，某学校两次选购同一种文具对贫困户学生进行慰问．第一次用1000元购进一批文具进行慰问，第二次购进时发现每件文具比第一次上涨了2.5元．学校用2500元购进了第二批文具，所购进文具的数量是第一次购进数量的2倍，问学校第二次购进了多少件文具？若设第一次购进文具数为x件，则可列方程（）

A、 $\frac{1000}{x} = \frac{2500}{2 x} + 2.5$ B、 $\frac{1000}{x} + \frac{2500}{2 x} = 2.5$ C、 $\frac{1000}{x} = \frac{2500}{2 x} - 2.5$ D、 $\frac{1000}{x} - 2.5 = \frac{2500}{2 x}$

查看试题解析
11. 如图，等边 $△ A B C$ 的三个顶点都在 $⊙ O$ 上， $A D$ 是 $⊙ O$ 的直径．若 $O A = 3$ ，则劣弧 $B D$ 的长是（）

A、 $\frac{π}{2}$ B、 $π$ C、 $\frac{3 π}{2}$ D、 $2 π$

查看试题解析
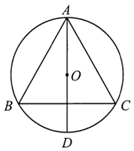12. 从－3，－1， $\frac{2}{3}$ ，1，2这五个数中，随机抽取一个数，记为a，若数a使关于x的不等式组 ${\begin{array}{l} \frac{1}{2} (3 x + 7) \geq 5 \\ x - a < 0 \end{array}$ 无解，且使关于x的一元一次方程 $a x + 3 = 5 - x$ 有整数解，那么这5个数中所有满足条件的a的值之和是（）

A、－2 B、 $- \frac{1}{2}$ C、－3 D、 $\frac{1}{2}$

查看试题解析

二、填空题

13. 某地一天中午12时的气温是 $7 ℃$ ，凌晨4时的气温比中午12时低 $8 ℃$ ，则凌晨4时的气温是 $℃$ ．

查看试题解析
14. 如图，直线 $a ∥ b$ ，且直线a，b被直线c所截，若 $∠ 1 = 30 °$ ，则 $∠ 2 =$ $°$ ．

查看试题解析
15. 因式分解： $a^{3} - a =$ ．

查看试题解析
16. 要使 $\frac{\sqrt{x + 1}}{2}$ 有意义，则x的取值范围为．

查看试题解析
17. 若反比例函数的图象经过点 $(- 3 ， 1)$ ，则该反比例函数的解析式为．

查看试题解析
18. 在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $C A = C B = 2$ ， D是 $△ A B C$ 所在平面内的一点，以A、B、C、D为顶点的四边形是平行四边形，则 $A D$ 的长为．

查看试题解析

三、解答题

19. 初中生的体育锻炼问题一直是教育工作者关注的问题之一，为此某县教育局对该县部分学校今年七年级学生的体育锻炼时间进行一次抽样调查（分为三个层级，A级：每天能坚持体育锻炼两个小时：B级：每天能参加体育锻炼一个小时；C级：每天很少进行体育锻炼），并将调查结果绘制成图1和图2的统计图（不完整）．请根据图中提供的信息，解答下列问题：

(1)、此次抽样调查中，共调查了名学生．

(2)、将图1补充完整；

(3)、求出图2中A级所占的圆心角的度数；

(4)、若每天参加体育锻炼时间一小时以上（含一小时）视为体育锻炼时间达标，根据抽样调查结果，请你估计该县近6000名初中生大约有多少名学生参加体育锻炼时间达标？

查看试题解析
20. 第24届冬奥会于2022年2月在北京市和张家口市联合举行．寒假期间某校组织部分滑雪爱好者参加“我是奥运小志愿者”活动，志愿者可以到“八达岭长城”、“世葡园”“龙庆峡”“百里画廊”四个景区之一参加活动．小明对“八达岭长城”和“百里画廊”最感兴趣，他将四个景区编号为甲、乙、丙、丁，并写在四张卡片上（除编号和内容不同之外，其余完全相同），他将卡片背面朝上，洗匀放好，从中随机抽取两张．

(1)、请用列表或画树状图的方法表示所有可能的结果．

(2)、求抽到的两张卡片恰好是“八达岭长城”和“百里画廊”的概率．

查看试题解析
21. 如图，在▱ABCD中，E，F分别是BC，AD中点．

(1)、求证：△ABE≌△CDF；

(2)、当BC=2AB=4，且△ABE的面积为 $\sqrt{3}$ ，求证：四边形AECF是菱形．

查看试题解析
22.
为更新果树品种，某果园计划新购进A、B两个品种的果树苗栽植培育，若计划购进这两种果树苗共45棵，其中A种苗的单价为7元/棵，购买B种苗所需费用y（元）与购买数量x（棵）之间存在如图所示的函数关系．

(1)、求y与x的函数关系式；

(2)、若在购买计划中，B种苗的数量不超过35棵，但不少于A种苗的数量，请设计购买方案，使总费用最低，并求出最低费用．

查看试题解析
23. 如图，已知 $⊙ O$ 的直径 $A B$ 与弦 $C D$ 相交于点E．且E为 $C D$ 中点，过点B作 $B F ∥ C D$ 交 $A D$ 的延长线于点F．

(1)、求证： $B F$ 是 $⊙ O$ 的切线．

(2)、连接 $B C$ ，若 $⊙ O$ 的半径为4， $s i n ∠ B C D = \frac{3}{4}$ ，求 $A D$ 、 $C D$ 的长．

查看试题解析
24. 如图，在直角坐标系中，直线y=﹣ $\frac{1}{3}$ x﹣1与x轴，y轴的交点分别为A、B，以x=﹣1为对称轴的抛物线y=x2+bx+c与x轴分别交于点A、C，直线x=﹣1与x轴交于点D．

(1)、求抛物线的解析式；

(2)、在线段AB上是否存在一点P，使以A，D，P为顶点的三角形与△AOB相似？若存在，求出点P的坐标；如果不存在，请说明理由；

(3)、若点Q在第三象限内，且tan∠AQD=2，线段CQ是否存在最小值，如果存在直接写出最小值；如果不存在，请说明理由．

查看试题解析

投中次数	5	7	8	9	10
人数	2	3	3	1	1