山西省运城市2022年中考第二次模拟考试数学试题

试卷更新日期：2022-07-13 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列各数中，比 $- 2$ 小的数是（）

A、-1.5 B、-2.5 C、 $- \sqrt{2}$ D、 $- \frac{4}{3}$

查看试题解析
2. 中国作为全球第二大经济体，FDP规模和美国保持着相对接近的水平，2021年我国GDP总量已经达到了17.7万亿美元，足足有日本的3倍多，将17.7万亿美元用科学记数法可表示为（）

A、 $17.7 \times 1 0^{12}$ 美元 B、 $1.77 \times 1 0^{12}$ 美元 C、 $1.77 \times 1 0^{13}$ 美元 D、 $1.77 \times 1 0^{14}$ 美元

查看试题解析
3. 下列运算正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $a^{3} - a^{2} = a$ C、 $a^{4} + a^{3} = a^{7}$ D、 ${(- a^{3} b^{4})}^{2} = a^{6} b^{8}$

查看试题解析
4. 如图，点O是△ABC的外心（三角形三边垂直平分线的交点），若∠BOC=96°，则∠A的度数为（）

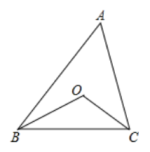A、49° B、47.5° C、48° D、不能确定

查看试题解析
5. 一个几何体的三视图如图所示，其中俯视图为正三角形，则该几何体的左视图中a的值为（）

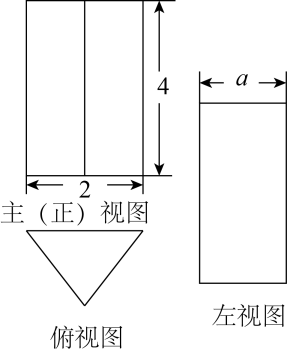A、2 B、 $\sqrt{3}$ C、1.7 D、1.8

查看试题解析
6. 李老师在求方程组 ${\begin{array}{l} x + y = 7 \\ x y = 6 \end{array}$ 的近似解时，先在平面直角坐标系中作出了一次函数 $y = - x ＋ 7$ 和反比例函数 $y = \frac{6}{x}$ 的图像（如图），接着观察这两个函数图象的交点坐标，然后得出该方程组的近似解，李老师的这种方法运用的主要数学思想是（）

A、公理化思想 B、分类讨论思想 C、整体思想 D、数形结合思想

查看试题解析
7. 已知关于x的一元二次方程ax²﹣4x﹣2＝0有实数根，则a的取值范围是（）

A、a≥﹣2 B、a＞﹣2 C、a≥﹣2且a≠0 D、a＞﹣2且a≠0

查看试题解析
8. 如图，在矩形ABCD中，点E是AD上一点，点F是BC上一点，将矩形ABCD沿直线EF折叠，点D的对应点为点 $D^{'}$ ，点C的对应点为点 $C^{'}$ ，若 $∠ 1 = 39 °$ ，则 $∠ 2$ 的度数是（）

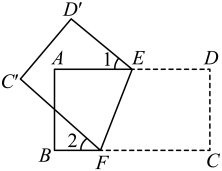A、39° B、51° C、41° D、70°

查看试题解析
9. 如图，将 $R t △ C A B$ 绕点B按逆时针方向旋转90°后，得到 $R t △ C^{'} A^{'} B$ ，已知 $∠ B A C = 90 °$ ， $∠ A B C = 60 °$ ， $B C = 2$ ，则图中阴影部分面积为（）

A、 $\frac{3}{4} π$ B、 $\frac{11}{12} π$ C、 $\frac{11}{12} π - \frac{\sqrt{3}}{2}$ D、 $\frac{6}{5} π$

查看试题解析
10. 如图，在 $R t △ O A B$ 中， $∠ O A B = 90 °$ ，点A在x轴的负半轴上，点B在第二象限，反比例函数 $y = \frac{k}{x} (x < 0)$ 的图象经过OB上一点D，与AB相交于点C，若 $O D = 2 B D$ ， $△ O B C$ 的面积为 $\frac{15}{8}$ ，则k的值是（）

A、 $- \frac{15}{4}$ B、-3 C、 $\frac{15}{4}$ D、3

查看试题解析

二、填空题

11. 不等式组 ${\begin{array}{l} 4 x - 6 < 5 x \\ \frac{x}{6} \leq - \frac{2}{3} \end{array}$ 的解集为．

查看试题解析
12. 一组按规律排列的式子 $a^{2}$ ， $a^{5}$ ， $a^{8}$ ， $a^{11}$ ， …，则第n个式子是．

查看试题解析
13. 体育承载着国家强盛，民族振兴的梦想，“双减”落地助力体育锻炼的升温，下面是某同学假期中间连续6天每天用于体育锻炼的时间（单位：分钟）：40，50，x，60，60，70．已知这组数据的平均数是50分钟，则这组数据的中位数是分钟．

查看试题解析
14. 如图，在正六边形ABCDEF的左边以AF为边作正五边形AFGHM，连接BM，则 $∠ A B M$ ，则 $∠ A B M$ 的度数为．

查看试题解析
15. 如图，在矩形ABCD中，E为BC边上一点， $A B = 2$ ，且 $∠ B A E = ∠ D A C$ ， $s i n ∠ C A E = \frac{3}{5}$ ，则CE的长为．

查看试题解析

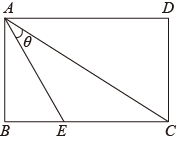
三、解答题

16.

(1)、计算： $| - \sqrt{8} | \times s i n 45 ° - {(- \frac{1}{2})}^{- 2} + {(- 2022)}^{0}$

(2)、下面是小华同学进行分式化简的过程，请认真阅读并完成相应的任务．
$\frac{a + 3}{a - 3} \cdot \frac{a^{2} + 3 a}{a^{2} + 6 a + 9} - \frac{3 a}{a^{2} - 9}$
$= \frac{a + 3}{a - 3} \cdot \frac{a (a + 3)}{{(a + 3)}^{2}} - \frac{3 a}{(a + 3) (a + 3)}$                     第一步
$= \frac{a}{a - 3} - \frac{3 a}{(a + 3) (a + 3)}$                            第二步
$= a (a + 3) - 3 a$                                  第三步
$= a^{2}$                                         第四步
任务一：填空：①以上化简步骤中，第二步是进行分式的约分，约分的依据是．
②第步开始出现不符合题意，这一步错误的原因是．
任务二：请直接写出该分式化简后的正确结果．

查看试题解析
17. 自2019年12月以来新型冠状病毒导致的肺炎疫情在全球蔓延流行，进入2022年，新一轮的疫情爆发又波及校园，严重危及师生的身心健康，为此某校师生举行了“疫情防控大演练”活动，并学习了当前疫情防控的主要措施，包括：（①远离感染源区；②加强自我防控；③增强身体体质；④合理健康饮食；⑤加强防控意识）五个要点，为了了解学生对“五要点”的掌握情况，从全校随机抽取了一部分学生作出调查，并根据学生的回答情况（A．仅能答出一点；B．仅能答出两点；C．能回答其中三点；D．能回答其中四点；E．能回答全部五点），绘制出下面两幅不完整的统计图，请根据统计图上的信息解答下列问题：

(1)、在这次调查中抽取的总人数为人．

(2)、在扇形统计图中“C”部分m的值为．

(3)、该学校共有学生1200人，估计能回答全部五个要点的人数约有多少人？

(4)、针对本次学习，学校准备组织一次疫情防控知识竞赛，要求每个班级选取两名同学参赛，小明和小颖所在的九年级某班共选出4名候选人，除小明和小颖之外还有另外2名同学，从这四人中随机选取两个人参加比赛，请用树状图或列表法求出恰好选中小明和小颖两人的概率（这4名学生分别用A，B，C，D表示，其中A，B分别代表小明和小颖）

查看试题解析
18. 关公是山西运城的名片，在解州常平关公故里的南山上有一尊世界上最高的关公铜像，他静静耸立在中条山间，远眺着河东大地，护佑着运城万民．数学实践小组想利用所学知识测量关公铜像的高度，下面是他们测量得到的相关数据：如图，他们在坡脚C测得铜像顶端A的仰角 $∠ A C E = 45 °$ ，然后沿坡面CB行走了一段距离到达D处，发现垂直距离升高了10米（即点D到CE的垂直距离为10米），在D处测得铜像顶端A的仰角 $∠ A D F = 53 °$ ，已知 $t a n ∠ B C E = \frac{1}{3}$ ，点A、B、C、D、E、F均在同一平面内， $A B ⊥ C E$ ， CE为地平线，请你根据以上数据，利用所学知识求出关公铜像AB的高度（参考数据： $s i n 53 ° = \frac{4}{5}$ ， $c o s 53 ° = \frac{3}{5}$ ， $c o s 53 ° = \frac{3}{5}$ ）

查看试题解析
19. 滨湖路是运城盐湖生态文化旅游南山片区串联滨湖各个功能的景观大道，是市民游憩、健身、出行的绿色廊道，可承担国家级马拉松、竞走、自行车等体育赛事，某绿化公司对其中一段长2400米的路边进行绿化，绿化800米后，为了尽快完成任务，后来每天的工作效率比原计划提高25%，结果共用26天完成绿化任务．

(1)、求原计划每天绿化多少米？

(2)、该绿化公司原来每天支付给工人的工资总额为1500元，为了完成整个工程后总共支付工人工资总额不超过43800元，求提高工作效率后每天支付给工人的工资总额最多可增长多少元？

查看试题解析
20. 阅读下列材料，并按要求解答相关问题：
【思考发现】根据直径所对的圆周角是直角，我们可以推出“如果一条定边所对的角始终为直角，那么所有满足条件的直角顶点组成的图形是以定边为直径的圆或圆弧（直径的两个端点除外）”这一正确的结论．
如图1，若AB是一条定线段，且 $∠ A P B = 90 °$ ，则所有满足条件的直角顶点P组成的图形是定边AB为直径的 $⊙ O$ （直径两端点A、B除外）

(1)、已知：如图2，四边形ABCD是边长为8的正方形，点E从点B出发向点C运动，同时点F从点C出发以相同的速度向点D运动，连接AE，BF相交于点P．
①当点E从点B运动到点C的过程中， $∠ A P B$ 的大小是否发生变化？若发生变化，请说明理由；若不发生变化，请直接写出 $∠ A P B$ 的度数．
②当点E从点B运动到点C的过程中，点P运动的路径是（）
A．线段；B．弧；C．半圆；D．圆
③点P运动的路经长是 ▲ ．

(2)、已知：如图3，在图2的条件下，连接CP，请直接写出E、F运动过程中，CP的最小值．

查看试题解析
21. 如图1，AB是 $⊙ O$ 的直径，点F是 $⊙ O$ 上的一点，连接AF，过点O作 $O C ∥ A F$ 交 $⊙ O$ 于点C，过点C作 $⊙ O$ 的切线，交FA的延长线于点D， $C E ⊥ A B$ 于E，连接AC．

(1)、求证： $A D = A E$ ；

(2)、如图2，在图1的条件下，若点F为半圆 $\overset{⌢}{A B}$ 的中点，连接CF交AB于点M，求 $∠ A M C$ 的度数．

查看试题解析
22. 将矩形ABCD对折，使AD与BC重合，得到折痕EF，展开后再一次折叠，使点A落在EF上的点 $A^{'}$ 处，并使得折痕经过点B，得到折痕BG，连接 $A A^{'}$ ，如图1，问题解决：

(1)、试判断图1中 $△ A B A^{'}$ 是什么特殊的三角形？并说明理由；

(2)、如图2，在图1的基础上， $A A^{'}$ 与BG相交于点N，点P是BN的中点，连接AP并延长交 $B A^{'}$ 于点Q，求 $\frac{B Q}{B A^{'}}$ 的值．

查看试题解析
23. 如图，已知抛物线 $y = a x^{2} + b x - 8$ 与x轴交于点 $A (- 2 ， 0)$ ， $B (8 ， 0)$ 两点，与y轴交于点C，点P是直线BC下方抛物线上一动点，过点P作直线 $P E ∥ y$ 轴，交直线BC于点D，交x轴于点F，以PD为斜边，在PD的右侧作等腰直角 $△ P D F$ ．

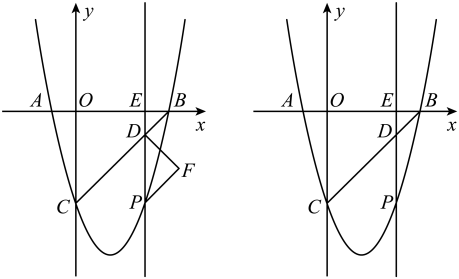(1)、求抛物线的表达式，并直接写出直线BC的表达式；

(2)、设点P的横坐标为m（ $0 < m < 3$ ），在点P运动的过程中，当等腰直角 $△ P D F$ 的面积为9时，请求出m的值；

(3)、连接AC，该抛物线上是否存在一点M，使 $∠ A C O ＋ ∠ B C M = ∠ A B C$ ，若存在，请直接写出所有符合条件的点M的坐标，若不存在，请说明理由．

查看试题解析