山西省阳泉市2022年中考考前教学质量检测(一模)数学试题
试卷更新日期:2022-07-13 类型:中考模拟
一、单选题
-
1. 在 , , 0,这四个数中,为无理数的是( )A、 B、 C、0 D、-22. 下列运算正确的是( )A、 B、 C、 D、3. 下列图形中,主视图为①的是( )
 A、
A、 B、
B、 C、
C、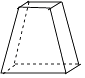 D、
D、 4. 北京作为全球首个双奥之城,于2月4日至2月20日举办第24届冬奥会,本届冬奥会汇聚了世界各国的运动员.伴随着中国以及数字媒体的发展,北京冬奥会创造了多项纪录:数字化互动最广泛的冬奥会、转播时长最长的冬奥会以及开幕式收视率最高的冬奥会.在赛事期间,创纪录的6400多万人使用奥林匹克网站和App关注冬奥会.数字6400万用科学记数法可表示为( )A、 B、 C、 D、5. 甲、乙、丙、丁四位同学五次数学测验成绩统计如右表所示,如果从这四位同学中,选出一位同学参加数学竞赛,那么应选___________去.
4. 北京作为全球首个双奥之城,于2月4日至2月20日举办第24届冬奥会,本届冬奥会汇聚了世界各国的运动员.伴随着中国以及数字媒体的发展,北京冬奥会创造了多项纪录:数字化互动最广泛的冬奥会、转播时长最长的冬奥会以及开幕式收视率最高的冬奥会.在赛事期间,创纪录的6400多万人使用奥林匹克网站和App关注冬奥会.数字6400万用科学记数法可表示为( )A、 B、 C、 D、5. 甲、乙、丙、丁四位同学五次数学测验成绩统计如右表所示,如果从这四位同学中,选出一位同学参加数学竞赛,那么应选___________去.甲
乙
丙
丁
平均分
85
90
90
85
方差
50
42
50
42
A、甲 B、乙 C、丙 D、丁6. 把不等式组中每个不等式的解集在同一条数轴上表示出来,正确的为( )A、 B、
B、 C、
C、 D、
D、 7. 如图,在“3×3”网格中,有3个涂成黑色的小方格.若再从余下的6个小方格中随机选取1个涂成黑色,则完成的图案为轴对称图案的概率是( )
7. 如图,在“3×3”网格中,有3个涂成黑色的小方格.若再从余下的6个小方格中随机选取1个涂成黑色,则完成的图案为轴对称图案的概率是( ) A、 B、 C、 D、8. 如图,点O为菱形ABCD的对角线AC,BD的交点,过点C作CE⊥AB于点E,连接OE,若OD=3,OE=2,则菱形ABCD的面积为( )
A、 B、 C、 D、8. 如图,点O为菱形ABCD的对角线AC,BD的交点,过点C作CE⊥AB于点E,连接OE,若OD=3,OE=2,则菱形ABCD的面积为( )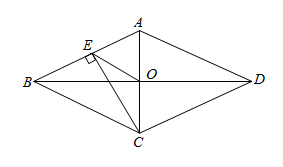 A、6 B、12 C、18 D、249. 如图,点P是反比例函数的图象上一点,过点P作PA⊥y轴于点A,点B是点A关于x轴的对称点,连接PB,若△PAB的面积为6,则k的值为( )
A、6 B、12 C、18 D、249. 如图,点P是反比例函数的图象上一点,过点P作PA⊥y轴于点A,点B是点A关于x轴的对称点,连接PB,若△PAB的面积为6,则k的值为( ) A、-3 B、6 C、-6 D、-1210. 如图,在扇形AOB中,∠AOB=120°,半径OC交弦AB于点D,且OC⊥OA.若 , 则阴影部分的面积为( )
A、-3 B、6 C、-6 D、-1210. 如图,在扇形AOB中,∠AOB=120°,半径OC交弦AB于点D,且OC⊥OA.若 , 则阴影部分的面积为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 方程组的解是 .12. 如图,含30°角的直角三角板的直角顶点C落在直尺下边沿上,60°角的顶点A落在直尺上边沿,直角边CD与直尺上边沿交于点B.若∠1=33°,则∠2= .
 13. 某中学有一块长30m,宽20m的矩形空地,计划在这块空地上划分出四分之一的区域种花,小明同学设计方案如图所示,求花带的宽度.设花带的宽为xm,则可列方程为 .
13. 某中学有一块长30m,宽20m的矩形空地,计划在这块空地上划分出四分之一的区域种花,小明同学设计方案如图所示,求花带的宽度.设花带的宽为xm,则可列方程为 .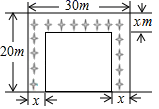 14. 如图,已知 是等腰三角形, 点D在AC边上,将 绕点A逆时针旋转45°得到 ,且点D′、D、B三点在同一条直线上,则 的度数是 .
14. 如图,已知 是等腰三角形, 点D在AC边上,将 绕点A逆时针旋转45°得到 ,且点D′、D、B三点在同一条直线上,则 的度数是 .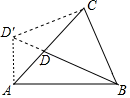 15. 如图,边长为的正方形ABCD中,点E为对角线BD上一点,连接CE,将CE绕点C顺时针旋转90°得到CF,连接EF和DF若EF=2BE,则BE的长为 .
15. 如图,边长为的正方形ABCD中,点E为对角线BD上一点,连接CE,将CE绕点C顺时针旋转90°得到CF,连接EF和DF若EF=2BE,则BE的长为 .
三、解答题
-
16. 计算及先化简求值(1)、;(2)、先化简 , 再选一个合适的x的值代入求值.17. 如图,点O为Rt△ABC的斜边BC上一点,以点O为圆心、OC为半径的⊙O与边AB相切于点D,与边AC,BC分别相交于点E,F,连接OE,DE,DF.
 (1)、求证:DE=DF;(2)、若∠B=30°,⊙O的半径为8,求AC的长.18. 某校组织了九年级学生进行“汉字听写大赛”,据统计,所有学生的比赛成绩均超过60分,最高分为100分.比赛的成绩分以下四个等级:A(),B(),C(),D()(单位:分).现随机抽取了九年级若干名学生的比赛成绩,绘制出如下不完整的统计图.请你结合以上信息,解答下列问题:
(1)、求证:DE=DF;(2)、若∠B=30°,⊙O的半径为8,求AC的长.18. 某校组织了九年级学生进行“汉字听写大赛”,据统计,所有学生的比赛成绩均超过60分,最高分为100分.比赛的成绩分以下四个等级:A(),B(),C(),D()(单位:分).现随机抽取了九年级若干名学生的比赛成绩,绘制出如下不完整的统计图.请你结合以上信息,解答下列问题: (1)、请补全比赛成绩直方图;(2)、针对本次统计结果,以下三位同学做出如下判断:
(1)、请补全比赛成绩直方图;(2)、针对本次统计结果,以下三位同学做出如下判断:小强认为:中位数落在B组;
小明认为:众数落在C组;
小亮认为:若C组有a人,则可估算平均成绩约为: .
以上判断中有一位同学是错误的 , 这位同学是(填“小强”、“小明”或“小亮”);
(3)、若该校九年级共1000名学生,测试成绩高于80分记为“优秀”,请你估计该校九年级学生中汉字听写比赛成绩达到“优秀”的人数.(4)、学校要求,各班需推荐一男一女两名学生参加总决赛,九年级(2)班班主任要在本班前五名同学(包括两名男生和三名女生)中进行推选,请用列表或树状图求恰好能按要求推选的概率是多少?19. 健康绿色生活,从饮用水开始!随着科技的发展和生活质量的不断提高,人们的自我保健意识也不断增强,对饮水品质的需求也越来越高.我市某公司根据市场需求代理A,B两种型号的净水器,每台A型净水器比每台B型净水器进价多200元,用5万元购进A型净水器与用4.5万元购进B型净水器的数量相等.(1)、求每台A型、B型净水器的进价各是多少元?(2)、该公司计划购进A、B两种型号的净水器共50台进行试销,其中A型净水器为x台,购买资金不超过9.8万元.试销时A型净水器每台售价2500元,B型净水器每台售价2180元,该公司决定从销售A型净水器的利润中按每台捐献75元作为公司帮扶贫困村饮水改造资金,设该公司售完50台净水器并捐献扶贫资金后获得的利润为W,求W的最大值.20. 随着科技的发展,越来越多高科技的产品应用在我们的生活中,智能跟踪监控摄像头就是其中的一种(如图1).一款被安装在某小区住宅楼铅直墙面l上A处的跟踪摄像头,在捕捉到地面上E处有一跟踪目标时,数据显示该目标到摄像头水平距离BE=8m,此时摄像头的俯视角度为35°;继续跟踪目标到达围墙CD的墙头D处,此时摄像头俯视角度减小了15°.已知围墙CD的铅直高度为1.8m,请求出目标落脚点D到墙面l的水平距离(结果保留到0.1m).(参考数据: , , , , , ) 21. 阅读下列材料,完成相应的学习任务.
21. 阅读下列材料,完成相应的学习任务.巧折黄金矩形
如果一个矩形宽与长的比为 , 那么这样的矩形叫做黄金矩形.
我们可以用如下方法折出黄金矩形:
如图,在矩形纸片ABCD中,AD=2.

操作1:将矩形纸片ABCD沿AF折叠,使得点D落在AB上的点E处,
展开得到折痕AF;
操作2:再将该矩形纸片折叠,使得点D与点F重合,展开得到折痕GH;
操作3:继续折叠该纸片,使得AG落在DC上,点A的对应点为点M,
点D的对应点为点P,折痕为GQ;
操作4:过点M折出DC的垂线,折痕为MN.
则四边形FENM是黄金矩形.
学习任务:
(1)、请你证明四边形FENM是黄金矩形;(2)、在不添加其他字母的情况下,请你再写出图中的一个黄金矩形.(参考数据:)22. 综合与实践【问题背景】
如图1,平行四边形ABCD中,∠B=60°,AB=6,AD=8.点E、G分别是AD和DC边的中点,过点E、G分别作DC和AD的平行线,两线交于点F,显然,四边形DEFG是平行四边形.

【独立思考】
(1)、线段AE和线段CG的数量关系是: .(2)、将平行四边形DEFG绕点D逆时针旋转,当DE落在DC边上时,如图2,连接AE和CG.①求AE的长;
②猜想AE与CG有怎样的数量关系,并证明你的猜想;
(3)、【问题解决】将平行四边形DEFG继续绕点D逆时针旋转,当A,E,F三点在同一直线上时(如图3),AE与CG交于点P,请直接写出线段CG的长和∠APC的度数.
23. 综合与探究如图,已知抛物线与x轴负半轴交于点 , 与y轴交于点 , 抛物线的顶点为D,直线y=x+b与抛物线交于A,F两点,过点D作DE∥y轴交直线AF于点E.
 (1)、求抛物线和直线AF的解析式;(2)、在直线AF上方的抛物线上有一点P,使 , 求点P的坐标;(3)、若点M为抛物线上一动点,试探究在直线AF上是否存在一点N,使得以D,E,M,N为顶点的四边形是平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
(1)、求抛物线和直线AF的解析式;(2)、在直线AF上方的抛物线上有一点P,使 , 求点P的坐标;(3)、若点M为抛物线上一动点,试探究在直线AF上是否存在一点N,使得以D,E,M,N为顶点的四边形是平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.