山东省淄博市高新区2022年中考二模数学试题
试卷更新日期:2022-07-13 类型:中考模拟
一、单选题
-
1. 在实数 , ,0,-1中,最小的数是( )A、-1 B、0 C、 D、2. 下列图形中,既是中心对称图形又是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如图是某天参观温州数学名人馆的学生人数统计图.若大学生有60人,则初中生有( )
3. 如图是某天参观温州数学名人馆的学生人数统计图.若大学生有60人,则初中生有( ) A、45人 B、75人 C、120人 D、300人4. 如图, 的顶点A,B,C的坐标分别是 ,则顶点D的坐标是( )
A、45人 B、75人 C、120人 D、300人4. 如图, 的顶点A,B,C的坐标分别是 ,则顶点D的坐标是( ) A、 B、 C、 D、5. 下列运算正确的是( )A、 B、 C、 D、6. 某地居民生活用水收费标准:每月用水量不超过17立方米,每立方米 元;超过部分每立方米 元.该地区某用户上月用水量为20立方米,则应缴水费为( )A、 元 B、 元 C、 元 D、 元7. 如图,∠BAC=36°,点O在边AB上,⊙O与边AC相切于点D,交边AB于点E,F,连接FD,则∠AFD等于( )
A、 B、 C、 D、5. 下列运算正确的是( )A、 B、 C、 D、6. 某地居民生活用水收费标准:每月用水量不超过17立方米,每立方米 元;超过部分每立方米 元.该地区某用户上月用水量为20立方米,则应缴水费为( )A、 元 B、 元 C、 元 D、 元7. 如图,∠BAC=36°,点O在边AB上,⊙O与边AC相切于点D,交边AB于点E,F,连接FD,则∠AFD等于( )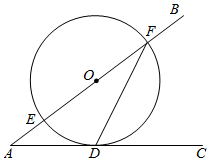 A、27° B、29° C、35° D、37°8. 化简:( )A、a﹣3 B、a+3 C、 D、9. 如图,在 中,AB=AC,分别以点A、B为圆心,以适当的长为半径作弧,两弧分别交于E,F,作直线EF,D为BC的中点,M为直线EF上任意一点.若BC=4, 面积为10,则BM+MD长度的最小值为( )
A、27° B、29° C、35° D、37°8. 化简:( )A、a﹣3 B、a+3 C、 D、9. 如图,在 中,AB=AC,分别以点A、B为圆心,以适当的长为半径作弧,两弧分别交于E,F,作直线EF,D为BC的中点,M为直线EF上任意一点.若BC=4, 面积为10,则BM+MD长度的最小值为( ) A、 B、3 C、4 D、510. 如图,在矩形ABCD中,点E在DC上,将矩形沿AE折叠,使点D落在BC边上的点F处.若AB=3,BC=5,则tan∠DAE的值为( )
A、 B、3 C、4 D、510. 如图,在矩形ABCD中,点E在DC上,将矩形沿AE折叠,使点D落在BC边上的点F处.若AB=3,BC=5,则tan∠DAE的值为( )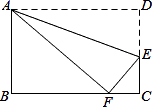 A、 B、 C、 D、11. 图(1),在 中, ,点P从点A出发,沿三角形的边以 /秒的速度逆时针运动一周,图(2)是点P运动时,线段 的长度y( )随运动时间x(秒)变化的关系图象,则图(2)中P点的坐标是( )
A、 B、 C、 D、11. 图(1),在 中, ,点P从点A出发,沿三角形的边以 /秒的速度逆时针运动一周,图(2)是点P运动时,线段 的长度y( )随运动时间x(秒)变化的关系图象,则图(2)中P点的坐标是( )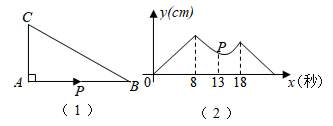 A、 B、 C、 D、12. 在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点 , 作正方形;延长交x轴于点 , 作正方形 , ….按照这样的规律,第2021个正方形的面积是( )
A、 B、 C、 D、12. 在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点 , 作正方形;延长交x轴于点 , 作正方形 , ….按照这样的规律,第2021个正方形的面积是( )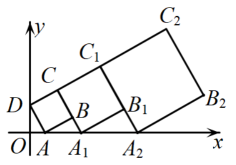 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 因式分解: .14. 如图,在正六边形ABCDEF中,分别以C , F为圆心,以边长为半径作弧,图中阴影部分的面积为24π,则正六边形的边长为 .
 15. 若关于 的一元二次方程 有两个不相等的实数根,则 的取值范围是.16. 如图,已知点A(2,0),B(0,4),C(2,4),D(6,6),连接AB,CD,将线段AB绕着某一点旋转一定角度,使其与线段CD重合(点A与点C重合,点B与点D重合),则这个旋转中心的坐标为 .
15. 若关于 的一元二次方程 有两个不相等的实数根,则 的取值范围是.16. 如图,已知点A(2,0),B(0,4),C(2,4),D(6,6),连接AB,CD,将线段AB绕着某一点旋转一定角度,使其与线段CD重合(点A与点C重合,点B与点D重合),则这个旋转中心的坐标为 .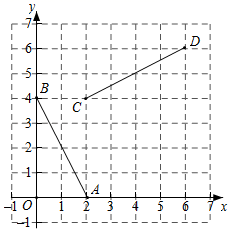 17. 如图,在矩形纸片ABCD中,AD=10,AB=8,将AB沿AE翻折,使点B落在 处,AE为折痕;再将EC沿EF翻折,使点C恰好落在线段EB'上的点 处,EF为折痕,连接 .若CF=3,则tan =.
17. 如图,在矩形纸片ABCD中,AD=10,AB=8,将AB沿AE翻折,使点B落在 处,AE为折痕;再将EC沿EF翻折,使点C恰好落在线段EB'上的点 处,EF为折痕,连接 .若CF=3,则tan =.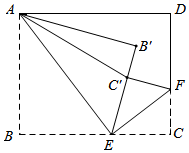
三、解答题
-
18. 解不等式组: , 并写出该不等式组的整数解.19. 如图, 是 的角平分线,在 上取点 ,使 .
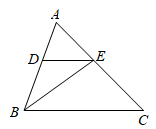 (1)、求证: .(2)、若 , ,求 的度数.20. 西安高新一中初中校区九年级有2000名学生,在体育中考前进行一次模拟体测,从中随机抽取部分学生,根据其测试成绩制作了下面两个统计图,请根据相关信息,解答下列问题:
(1)、求证: .(2)、若 , ,求 的度数.20. 西安高新一中初中校区九年级有2000名学生,在体育中考前进行一次模拟体测,从中随机抽取部分学生,根据其测试成绩制作了下面两个统计图,请根据相关信息,解答下列问题:
(Ⅰ)本次抽取到的学生人数为 ▲ , 图2中m的值为 ▲ ;
(Ⅱ)求出本次调查获取的样本数据的平均数、众数和中位数;
(Ⅲ)根据样本数据,估计我校九年级模拟体测中不低于11分的学生约有多少人?
21. 如图,平面直角坐标系xOy中,▱OABC的边OC在x轴上,对角线AC,OB交于点M,函数y=(x>0)的图象经过点A(3,4)和点M. (1)、求k的值和点M的坐标;(2)、求▱OABC的周长.22. 某公司生产的一种营养品信息如下表.已知甲食材每千克的进价是乙食材的2倍,用80元购买的甲食材比用20元购买的乙食材多1千克.
(1)、求k的值和点M的坐标;(2)、求▱OABC的周长.22. 某公司生产的一种营养品信息如下表.已知甲食材每千克的进价是乙食材的2倍,用80元购买的甲食材比用20元购买的乙食材多1千克.营养品信息表
营养成分
每千克含铁42毫克
配料表
原料
每千克含铁
甲食材
50毫克
乙食材
10毫克
规格
每包食材含量
每包单价
A包装
1千克
45元
B包装
0.25千克
12元
(1)、问甲、乙两种食材每千克进价分别是多少元?(2)、该公司每日用18000元购进甲、乙两种食材并恰好全部用完.①问每日购进甲、乙两种食材各多少千克?
②已知每日其他费用为2000元,且生产的营养品当日全部售出.若A的数量不低于B的数量,则A为多少包时,每日所获总利润最大?最大总利润为多少元?
23. 如图,⊙O为等边△ABC的外接圆,半径为2,点D在劣弧 上运动(不与点A,B重合),连接DA,DB,DC.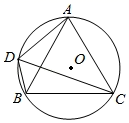 (1)、求证:DC是∠ADB的平分线;(2)、四边形ADBC的面积S是线段DC的长x的函数吗?如果是,求出函数解析式;如果不是,请说明理由;(3)、若点M,N分别在线段CA,CB上运动(不含端点),经过探究发现,点D运动到每一个确定的位置,△DMN的周长有最小值t,随着点D的运动,t的值会发生变化,求所有t值中的最大值.24. 将一张三角形纸片ABC放置在如图所示的平面直角坐标系中,点A(﹣6,0),点B(0,2),点C(﹣4,8),二次函数y=ax2+bx+c(a≠0)的图象经过点A,B,该抛物线的对称轴经过点C,顶点为D.
(1)、求证:DC是∠ADB的平分线;(2)、四边形ADBC的面积S是线段DC的长x的函数吗?如果是,求出函数解析式;如果不是,请说明理由;(3)、若点M,N分别在线段CA,CB上运动(不含端点),经过探究发现,点D运动到每一个确定的位置,△DMN的周长有最小值t,随着点D的运动,t的值会发生变化,求所有t值中的最大值.24. 将一张三角形纸片ABC放置在如图所示的平面直角坐标系中,点A(﹣6,0),点B(0,2),点C(﹣4,8),二次函数y=ax2+bx+c(a≠0)的图象经过点A,B,该抛物线的对称轴经过点C,顶点为D.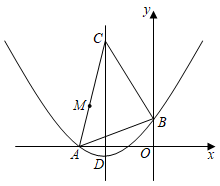 (1)、求该二次函数的表达式及点D的坐标;(2)、点M在边AC上(异于点A,C),将三角形纸片ABC折叠,使得点A落在直线AB上,且点M落在边BC上,点M的对应点记为点N,折痕所在直线l交抛物线的对称轴于点P,然后将纸片展开.
(1)、求该二次函数的表达式及点D的坐标;(2)、点M在边AC上(异于点A,C),将三角形纸片ABC折叠,使得点A落在直线AB上,且点M落在边BC上,点M的对应点记为点N,折痕所在直线l交抛物线的对称轴于点P,然后将纸片展开.①请作出图中点M的对应点N和折痕所在直线l;(要求:尺规作图,不写作法,保留作图痕迹)
②连接MP,NP,在下列选项中:A.折痕与AB垂直,B.折痕与MN的交点可以落在抛物线的对称轴上,C.= , D.= , 所有正确选项的序号是 ▲ .
③点Q在二次函数y=ax2+bx+c(a≠0)的图象上,当PDQ∼PMN时,求点Q的坐标.