山东省枣庄市薛城区2022年九年级中考数学模拟试题
试卷更新日期:2022-07-13 类型:中考模拟
一、单选题
-
1. 如图所示,该几何体的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 在今年举行的第127届“广交会”上,有近26000家厂家进行“云端销售”.其中数据26000用科学记数法表示为( )A、26×103 B、2.6×103 C、2.6×104 D、0.26×1053. 如图, 内接于圆, ,过点C的切线交 的延长线于点 .则 ( )
2. 在今年举行的第127届“广交会”上,有近26000家厂家进行“云端销售”.其中数据26000用科学记数法表示为( )A、26×103 B、2.6×103 C、2.6×104 D、0.26×1053. 如图, 内接于圆, ,过点C的切线交 的延长线于点 .则 ( )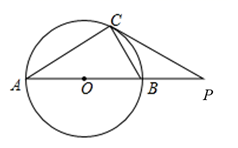 A、 B、 C、 D、4. 若 =2 , =3 ,则a+b之值为何?( )A、13 B、17 C、24 D、405. 已知关于x的一元二次方程(m-1)x2+2x+1=0有实数根,则m的取值范围是( )A、m<2 B、m≤2 C、m<2且m≠1 D、m≤2且m≠16. 箱子内装有53颗白球及2颗红球,小芬打算从箱子内抽球,以每次抽出一球后将球再放回的方式抽53次球.若箱子内每颗球被抽到的机会相等,且前52次中抽到白球51次及红球1次,则第53次抽球时,小芬抽到红球的机率为何?( )A、 B、 C、 D、7. 如图,在菱形ABCD中,AB=5,AC=6,过点D作DE⊥BA,交BA的延长线于点E,则线段DE的长为( )
A、 B、 C、 D、4. 若 =2 , =3 ,则a+b之值为何?( )A、13 B、17 C、24 D、405. 已知关于x的一元二次方程(m-1)x2+2x+1=0有实数根,则m的取值范围是( )A、m<2 B、m≤2 C、m<2且m≠1 D、m≤2且m≠16. 箱子内装有53颗白球及2颗红球,小芬打算从箱子内抽球,以每次抽出一球后将球再放回的方式抽53次球.若箱子内每颗球被抽到的机会相等,且前52次中抽到白球51次及红球1次,则第53次抽球时,小芬抽到红球的机率为何?( )A、 B、 C、 D、7. 如图,在菱形ABCD中,AB=5,AC=6,过点D作DE⊥BA,交BA的延长线于点E,则线段DE的长为( )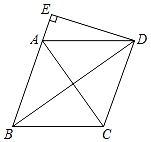 A、 B、 C、4 D、8. 如图,为了测量一条河流的宽度,一测量员在河岸边相距200米的P、Q两点分别测定对岸一棵树T的位置,T在P的正北方向,且T在Q的北偏西70°方向,则河宽(PT的长)可以表示为( )
A、 B、 C、4 D、8. 如图,为了测量一条河流的宽度,一测量员在河岸边相距200米的P、Q两点分别测定对岸一棵树T的位置,T在P的正北方向,且T在Q的北偏西70°方向,则河宽(PT的长)可以表示为( )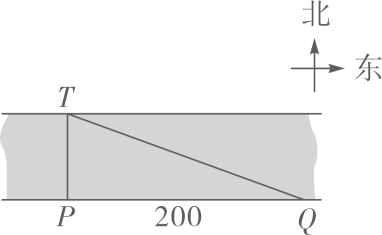 A、200tan70°米 B、 米 C、200sin70°米 D、 米9. 如图,点A在反比例函数 的图象上,过点A作 轴,垂足为B,交反比例函数 的图象于点C.P为y轴上一点,连接 , .则 的面积为( )
A、200tan70°米 B、 米 C、200sin70°米 D、 米9. 如图,点A在反比例函数 的图象上,过点A作 轴,垂足为B,交反比例函数 的图象于点C.P为y轴上一点,连接 , .则 的面积为( ) A、5 B、6 C、11 D、1210. 如图①,正方形 中, , 相交于点O,E是 的中点,动点P从点E出发,沿着 的路径以每秒1个单位长度的速度运动到点A,在此过程中线段 的长度 随着运动时间x的函数关系如图②所示,则 的长为( )
A、5 B、6 C、11 D、1210. 如图①,正方形 中, , 相交于点O,E是 的中点,动点P从点E出发,沿着 的路径以每秒1个单位长度的速度运动到点A,在此过程中线段 的长度 随着运动时间x的函数关系如图②所示,则 的长为( ) A、 B、4 C、 D、11. 下列各正方形中的四个数之间都有相同的规律,根据此规律,x的值为( )
A、 B、4 C、 D、11. 下列各正方形中的四个数之间都有相同的规律,根据此规律,x的值为( )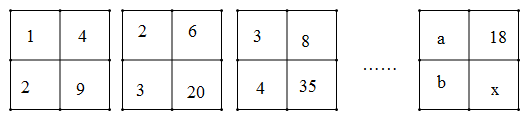 A、135 B、153 C、170 D、18912. 如图,已知抛物线 的对称轴为直线 .给出下列结论:
A、135 B、153 C、170 D、18912. 如图,已知抛物线 的对称轴为直线 .给出下列结论: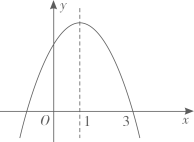
① ; ② ; ③ ; ④ .
其中,正确的结论有( )
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 函数 中自变量x的取值范围是 .
14. 如图,将周长为10的△ABC沿BC方向平移2个单位长度得到△DEF,则四边形ABFD的周长为 .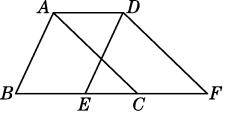 15. 如图,在边长为2的正方形ABCD中,对角线AC的中点为O,分别以点A,C为圆心,以AO的长为半径画弧,分别与正方形的边相交,则图中的阴影部分的面积为.(结果保留π)
15. 如图,在边长为2的正方形ABCD中,对角线AC的中点为O,分别以点A,C为圆心,以AO的长为半径画弧,分别与正方形的边相交,则图中的阴影部分的面积为.(结果保留π)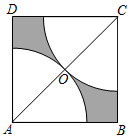 16. 对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形ABCD,对角线AC、BD交于点O.若AD=3,BC=5,则 .
16. 对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形ABCD,对角线AC、BD交于点O.若AD=3,BC=5,则 .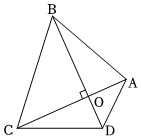 17. 竖直上抛物体时,物体离地而的高度与运运动时间之间的关系可以近似地用公式表示,其中是物体抛出时高地面的高度,是物体抛出时的速度.某人将一个小球从距地面的高处以的速度竖直向上抛出,小球达到的离地面的最大高度为m.18. 如图, 内接于 于点H,若 , 的半径为7,则 .
17. 竖直上抛物体时,物体离地而的高度与运运动时间之间的关系可以近似地用公式表示,其中是物体抛出时高地面的高度,是物体抛出时的速度.某人将一个小球从距地面的高处以的速度竖直向上抛出,小球达到的离地面的最大高度为m.18. 如图, 内接于 于点H,若 , 的半径为7,则 .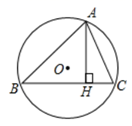
三、解答题
-
19. 计算:(1)、计算:(2)、先化简, , 然后从范围内选取一个合适的整数作为x的值代入求值.20. 位于河南省登封市境内的元代观星台,是中国现存最早的天文台,也是世界文化遗产之一.

某校数学社团的同学们使用卷尺和自制的测角仪测量观星台的高度.如图所示,他们在地面一条水 平步道 上架设测角仪,先在点M处测得观星台最高点A的仰角为 ,然后沿 方向前进 到达点N处,测得点 的仰角为 .测角仪的高度为 ,
(1)、求观星台最高点A距离地面的高度(结果精确到 .参考数据: );(2)、“景点简介”显示,观星台的高度为 ,请计算本次测量结果的误差,并提出一条减小误差的合理化建议.21. 端午节是中国的传统节日.今年端午节前夕,遂宁市某食品厂抽样调查了河东某居民区市民对A、B、C、D四种不同口味粽子样品的喜爱情况,并将调查情况绘制成如图两幅不完整统计图: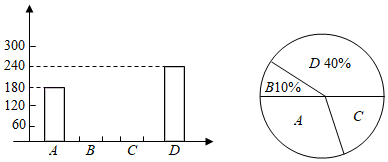 (1)、本次参加抽样调查的居民有人.(2)、喜欢C种口味粽子的人数所占圆心角为 ▲ 度.根据题中信息补全条形统计图.(3)、若该居民小区有6000人,请你估计爱吃D种粽子的有人.(4)、若有外型完全相同的A、B、C、D棕子各一个,煮熟后,小李吃了两个,请用列表或画树状图的方法求他第二个吃的粽子恰好是A种粽子的概率.22. 如图,已知 , 是一次函数 和反比例函数 的图象的两个交点.
(1)、本次参加抽样调查的居民有人.(2)、喜欢C种口味粽子的人数所占圆心角为 ▲ 度.根据题中信息补全条形统计图.(3)、若该居民小区有6000人,请你估计爱吃D种粽子的有人.(4)、若有外型完全相同的A、B、C、D棕子各一个,煮熟后,小李吃了两个,请用列表或画树状图的方法求他第二个吃的粽子恰好是A种粽子的概率.22. 如图,已知 , 是一次函数 和反比例函数 的图象的两个交点.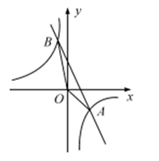 (1)、求反比例函数和一次函数的解析式;(2)、求 的面积;(3)、直接写出关于 的不等式 的解集.23. 如图,在 中, ,以 的边 为直径作 ,交 于点 ,过点 作 ,垂足为点 .
(1)、求反比例函数和一次函数的解析式;(2)、求 的面积;(3)、直接写出关于 的不等式 的解集.23. 如图,在 中, ,以 的边 为直径作 ,交 于点 ,过点 作 ,垂足为点 .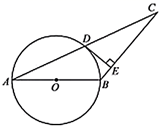 (1)、试证明 是 的切线;(2)、若 的半径为5, ,求此时 的长.24. 如图1,△ABC和△DCE都是等边三角形.
(1)、试证明 是 的切线;(2)、若 的半径为5, ,求此时 的长.24. 如图1,△ABC和△DCE都是等边三角形.探究发现
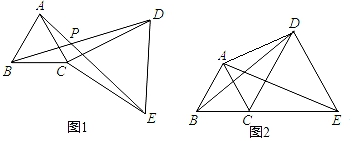 (1)、△BCD与△ACE是否全等?若全等,加以证明;若不全等,请说明理由.
(1)、△BCD与△ACE是否全等?若全等,加以证明;若不全等,请说明理由.拓展运用
(2)、若B、C、E三点不在一条直线上,∠ADC=30°,AD=3,CD=2,求BD的长.(3)、若B、C、E三点在一条直线上(如图2),且△ABC和△DCE的边长分别为1和2,求△ACD的面积及AD的长.25. 如图,抛物线y=ax2+bx+2与x轴交于A,B两点,且OA=2OB,与y轴交于点C,连接BC,抛物线对称轴为直线x= ,D为第一象限内抛物线上一动点,过点D作DE⊥OA于点E,与AC交于点F,设点D的横坐标为m.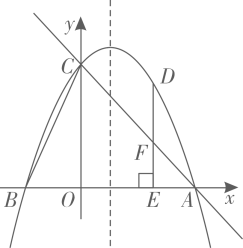 (1)、求抛物线的表达式;(2)、当线段DF的长度最大时,求D点的坐标;(3)、抛物线上是否存在点D,使得以点O,D,E为顶点的三角形与 相似?若存在,求出m的值;若不存在,请说明理由.
(1)、求抛物线的表达式;(2)、当线段DF的长度最大时,求D点的坐标;(3)、抛物线上是否存在点D,使得以点O,D,E为顶点的三角形与 相似?若存在,求出m的值;若不存在,请说明理由.