山东省枣庄市台儿庄区2022年中考二模数学试题
试卷更新日期:2022-07-13 类型:中考模拟
一、单选题
-
1. 下列计算正确的是( )A、 B、 C、 D、2. 到2021年6月3日,我国31个省(自治区、直辖市)和新疆生产建设兵团,累计接种新冠疫苗约7.05亿剂次,请将7.05亿用科学记数法表示( )A、 B、 C、 D、3. 如图, ,点 在 边上,已知 ,则 的度数为( )
 A、 B、 C、 D、4. 为了向建党一百周年献礼,我市中小学生开展了红色经典故事演讲比赛.某参赛小组6名同学的成绩(单位:分)分别为:85,82,86,82,83,92.关于这组数据,下列说法错误的是( )A、众数是82 B、中位数是84 C、方差是84 D、平均数是855. 若关于x的分式方程的解是非负数,则的取值范围是( )A、 B、b≤6且b≠4 C、b<6且b≠4 D、b<66. 定义:若 , 则 , x称为以10为底的N的对数,简记为 , 其满足运算法则: . 例如:因为 , 所以 , 亦即; . 根据上述定义和运算法则,计算的结果为( )A、5 B、2 C、1 D、07. 一次函数 的图象与x轴交于点B,与反比例函数 的图象交于点 ,且 的面积为1,则m的值是( )A、1 B、2 C、3 D、48. 如图,为⊙O的直径,弦于点E,直线l切⊙O于点C,延长交l于点F,若 , , 则的长度为( )
A、 B、 C、 D、4. 为了向建党一百周年献礼,我市中小学生开展了红色经典故事演讲比赛.某参赛小组6名同学的成绩(单位:分)分别为:85,82,86,82,83,92.关于这组数据,下列说法错误的是( )A、众数是82 B、中位数是84 C、方差是84 D、平均数是855. 若关于x的分式方程的解是非负数,则的取值范围是( )A、 B、b≤6且b≠4 C、b<6且b≠4 D、b<66. 定义:若 , 则 , x称为以10为底的N的对数,简记为 , 其满足运算法则: . 例如:因为 , 所以 , 亦即; . 根据上述定义和运算法则,计算的结果为( )A、5 B、2 C、1 D、07. 一次函数 的图象与x轴交于点B,与反比例函数 的图象交于点 ,且 的面积为1,则m的值是( )A、1 B、2 C、3 D、48. 如图,为⊙O的直径,弦于点E,直线l切⊙O于点C,延长交l于点F,若 , , 则的长度为( )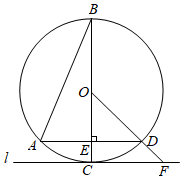 A、2 B、 C、 D、49. 如图,在菱形 中,P是对角线 上一动点,过点P作 于点E. 于点F.若菱形 的周长为20,面积为24,则 的值为( )
A、2 B、 C、 D、49. 如图,在菱形 中,P是对角线 上一动点,过点P作 于点E. 于点F.若菱形 的周长为20,面积为24,则 的值为( ) A、4 B、 C、6 D、10. 二次函数 的图象的一部分如图所示.已知图象经过点 ,其对称轴为直线 .下列结论:① ;② ;③ ;④若抛物线经过点 ,则关于 的一元二次方程 的两根分别为 ,5,上述结论中正确结论的个数为( )
A、4 B、 C、6 D、10. 二次函数 的图象的一部分如图所示.已知图象经过点 ,其对称轴为直线 .下列结论:① ;② ;③ ;④若抛物线经过点 ,则关于 的一元二次方程 的两根分别为 ,5,上述结论中正确结论的个数为( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 若式子在实数范围内有意义,则x的取值范围是 .12. 三角形三边的长是2、5、m,则 = .13. 如图,点A是反比例函数y=(x>0)的图象上一点,过点A作AC⊥x轴于点C,AC交反比例函数y=(x>0)的图象于点B,点P是y轴正半轴上一点.若△PAB的面积为2,则k的值为 .
 14. 如图,平面直角坐标系xOy中,点A的坐标为(8,5),⊙A与x轴相切,点P在y轴正半轴上,PB与⊙A相切于点B.若∠APB=30°,则点P的坐标为 .
14. 如图,平面直角坐标系xOy中,点A的坐标为(8,5),⊙A与x轴相切,点P在y轴正半轴上,PB与⊙A相切于点B.若∠APB=30°,则点P的坐标为 .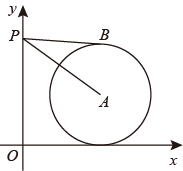 15. 如图,在中, , , , 交于点 . 点为线段上的动点,则的最小值为 .
15. 如图,在中, , , , 交于点 . 点为线段上的动点,则的最小值为 .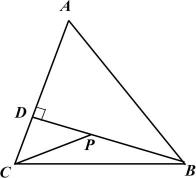 16. 观察等式:2+22=23﹣2,2+22+23=24﹣2,2+22+23+24=25﹣2,…,已知按一定规律排列的一组数:2100 , 2101 , 2102 , …,2199 , 若2100=m,用含m的代数式表示这组数的和是 .
16. 观察等式:2+22=23﹣2,2+22+23=24﹣2,2+22+23+24=25﹣2,…,已知按一定规律排列的一组数:2100 , 2101 , 2102 , …,2199 , 若2100=m,用含m的代数式表示这组数的和是 .三、解答题
-
17. 已知 ,求A、B的值.18. 某校开展了“禁毒”知识的宣传教育活动.为了解这次活动的效果,现随机抽取部分学生进行知识测试,并将所得数据绘制成如下不完整的统计图表:
等级
频数(人数)
频率
优秀
60
0.6
良好
a
0.25
合格
10
b
基本合格
5
0.05
合计
c
1
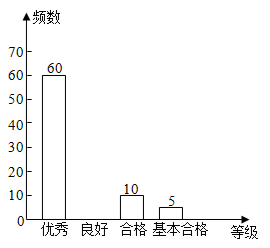
根据统计图表提供的信息,解答下列问题:
(1)、a= , b= , c=;(2)、补全条形统计图;(3)、该学校共有1600名学生,估计测试成绩等级在合格以上(包括合格)的学生约有多少人?(4)、在这次测试中,九年级(3)班的甲,乙、丙、丁四位同学的成绩均为“优秀”,现班主任准备从这四名同学中随机选取两名同学出一期“禁毒”知识的黑板报,请用列表法成画树状图法求甲、乙两名同学同时被选中的概率.19. 如图,一次函数y=kx﹣2k(k≠0)的图象与反比例函数(m﹣1≠0)的图象交于点C,与x轴交于点A,过点C作CB⊥y轴,垂足为B,若S△ABC=3 (1)、求点A的坐标及m的值;(2)、若AB= , 求一次函数的表达式.20. 如图,点E为正方形 外一点, ,将 绕A点逆时针方向旋转 得到 的延长线交 于H点.
(1)、求点A的坐标及m的值;(2)、若AB= , 求一次函数的表达式.20. 如图,点E为正方形 外一点, ,将 绕A点逆时针方向旋转 得到 的延长线交 于H点. (1)、试判定四边形 的形状,并说明理由;(2)、已知 ,求 的长.21. “通过等价变换,化陌生为熟悉,化未知为已知”是数学学习中解决问题的基本思维方式,例如:解方程 ,就可以利用该思维方式,设 ,将原方程转化为: 这个熟悉的关于y的一元二次方程,解出y,再求x,这种方法又叫“换元法”.请你用这种思维方式和换元法解决下面的问题.已知实数x,y满足 ,求 的值.22. 如图,点C是以AB为直径的⊙O上一点,D是AB延长线上一点,过点D作BD垂线交AC延长线于点E,连接CD且CD=ED.
(1)、试判定四边形 的形状,并说明理由;(2)、已知 ,求 的长.21. “通过等价变换,化陌生为熟悉,化未知为已知”是数学学习中解决问题的基本思维方式,例如:解方程 ,就可以利用该思维方式,设 ,将原方程转化为: 这个熟悉的关于y的一元二次方程,解出y,再求x,这种方法又叫“换元法”.请你用这种思维方式和换元法解决下面的问题.已知实数x,y满足 ,求 的值.22. 如图,点C是以AB为直径的⊙O上一点,D是AB延长线上一点,过点D作BD垂线交AC延长线于点E,连接CD且CD=ED. (1)、求证:CD是⊙O的切线;(2)、若tan∠DCE=2,BD=1,求⊙O的半径.23. 如图
(1)、求证:CD是⊙O的切线;(2)、若tan∠DCE=2,BD=1,求⊙O的半径.23. 如图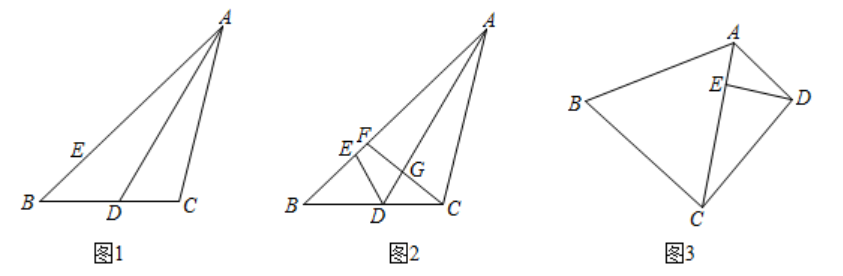 (1)、(证明体验)
(1)、(证明体验)如图1, 为 的角平分线, ,点E在 上, .求证: 平分 .
(2)、(思考探究)如图2,在(1)的条件下,F为 上一点,连结 交 于点G.若 , , ,求 的长.
(3)、(拓展延伸)如图3,在四边形 中,对角线 平分 ,点E在 上, .若 ,求 的长.
24. 如图,已知抛物线 与x轴交于点A(1,0)和B,与y轴交于点C,对称轴为 .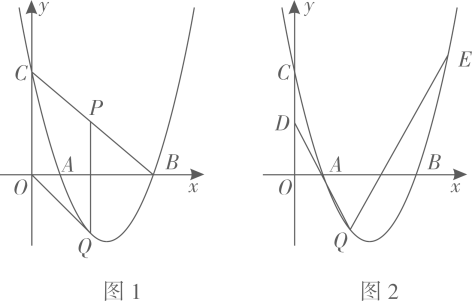 (1)、求抛物线的解析式;(2)、如图1,若点P是线段BC上的一个动点(不与点B,C重合),过点P作y轴的平行线交抛物线于点Q,连接OQ.当线段PQ长度最大时,判断四边形OCPQ的形状并说明理由.(3)、如图2,在(2)的条件下,D是OC的中点,过点Q的直线与抛物线交于点E,且 .在y轴上是否存在点F,使得 为等腰三角形?若存在,求点F的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、如图1,若点P是线段BC上的一个动点(不与点B,C重合),过点P作y轴的平行线交抛物线于点Q,连接OQ.当线段PQ长度最大时,判断四边形OCPQ的形状并说明理由.(3)、如图2,在(2)的条件下,D是OC的中点,过点Q的直线与抛物线交于点E,且 .在y轴上是否存在点F,使得 为等腰三角形?若存在,求点F的坐标;若不存在,请说明理由.