山东省潍坊市诸城市2022年中考二模数学试题

试卷更新日期：2022-07-13 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 华为麒麟990芯片采用了最新的0.000000007米的工艺制程，数0.000000007用科学记数法表示为（）

A、7×10^﹣9 B、7×10^﹣8 C、0.7×10^﹣9 D、0.7×10^﹣8

查看试题解析
3. 如图，所给三视图的几何体是（）

A、球 B、圆柱 C、圆锥 D、三棱锥

查看试题解析
4. 如图，AB//CD，EF＝DF，若∠A＝50°，则∠E 等于（）

A、50° B、55° C、60° D、65°

查看试题解析
5. 关于 $x$ 的方程 $x^{2} + x + k = 0$ 有两个相等的实数根，则 $\sqrt{k + 1} =$ （）

A、 $\frac{3}{4}$ B、 $\frac{\sqrt{3}}{2}$ C、 $\frac{5}{4}$ D、 $\frac{\sqrt{5}}{2}$

查看试题解析
6. 如图，按照程序图计算，当输入正整数x时，输出的结果是215，则输入的x的值可能（）

A、6 B、7 C、8 D、9

查看试题解析
7. 如图，A，B是反比例函数 $y = \frac{k}{x} (k > 0)$ 在第一象限内的图象上的两点，且A，B两点的横坐标分别是2和4， $S_{△ A O B} = 3$ ，则k的值为（）

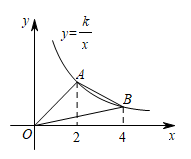A、4 B、3 C、2 D、1

查看试题解析
8. 已知：四边形ABCD中，AB=2，CD=3，M、N分别是AD，BC的中点，则线段MN的取值范围是（）

A、1＜MN＜5 B、1＜MN≤5 C、 $\frac{1}{2}$ ＜MN＜ $\frac{5}{2}$ D、 $\frac{1}{2}$ ＜MN≤ $\frac{5}{2}$

查看试题解析

二、多选题

9. 如图所示，数轴上点 $A$ ， $B$ 对应的数分别为 $a$ ， $b$ ，下列关系式正确的是（）

A、 $a^{2} > b^{2}$ B、 $\sqrt[3]{- a b} < 0$ C、 $\frac{1}{a} - \frac{1}{b} > 0$ D、 $a - b > 0$

查看试题解析
10. 为了解某校九年级800名学生的跳绳情况（60秒跳绳的次数），随机对该年级50名学生进行了调查，根据收集的数据绘制了如图所示的频数分布直方图（每组数据包括左端值不包括右端值，如最左边第一组的次数 $x$ 为： $60 \leq x < 80$ ），则以下说法正确的是（）

A、跳绳次数不少于100次的占80% B、大多数学生跳绳次数在140~160范围内 C、跳绳次数最多的是160次 D、由样本可以估计全年级800人中跳绳次数在60~80次的大约有64人

查看试题解析
11. 张华、李颖两人沿同一条笔直的公路相向而行，张华从甲地前往乙地，李颖从乙地前往甲地．张华先出发3分钟后李颖才出发，当张华行驶到6分钟时发现重要物品忘带，立刻以原速 $\frac{3}{2}$ 的掉头返回甲地．拿到物品后以提速后的速度继续前往乙地，二人相距的路程 $y$ （米）与张华出发的时间 $x$ （分钟）之间的关系如图所示，下列说法正确的是（）

A、李颖速度是张华提速前速度的 $\frac{3}{2}$ B、李颖的速度为 $240 m / m i n$ C、两人第一次相遇的时间是 $\frac{89}{6}$ 分钟 D、张华最终达到乙地的时间是 $\frac{85}{3}$ 分钟

查看试题解析
12. 如图，在 $△ A B C$ 中， $∠ A B C$ 和 $∠ A C B$ 的角平分线交于点 $O$ ， $A D$ 经过点 $O$ 与 $B C$ 交于 $D$ ，以 $A D$ 为边向两侧作等边 $△ A D E$ 和等边 $△ A D F$ ，分别和 $A B$ ， $A C$ 交于 $G$ ， $H$ 连接 $G H$ ．若 $∠ B O C = 120 °$ ， $A B = a$ ， $A C = b$ ， $A D = c$ ．则下列结论中正确的是（）

A、 $∠ B A C = 60 °$ B、 $△ A G H$ 是等边三角形 C、 $A D$ 与 $G H$ 互相垂直平分 D、 $S_{△ A B C} = \frac{1}{4} (a + b) c$

查看试题解析

三、填空题

13. 某医院要从 $A$ ， $B$ ， $C$ 三名志愿者中任意抽调两人助力全民核酸检测工作，恰好抽到志愿者 $B$ 和 $C$ 的概率是．

查看试题解析
14. 如图，在过点 $P$ 作直线 $a$ 的垂线时，小颖先将一圆形透明纸片对折得到折痕 $A B$ ，然后让端点 $A$ 与点 $P$ 重合，端点 $B$ 落在直线 $a$ 上，标出直线 $a$ 与圆形纸片的交点 $C$ ，连接 $A C$ ，则 $A C ⊥ a$ ．她的作图依据是．

查看试题解析
15. 若关于x的分式方程 $\frac{2 x}{x - 1} - 3 = \frac{m}{1 - x}$ 的解为正数，则m的取值范围是.

查看试题解析
16. 二次函数 $y = \frac{1}{2} x^{2} + \frac{1}{2} x$ 的图像如图所示，点 $A_{1} 、 A_{2} 、 A_{3} 、 A_{4} 、 ⋯ ⋯ 、 A_{2022}$ 在二次函数 $y = \frac{1}{2} x^{2} + \frac{1}{2} x$ 位于第一象限的图像上，点 $B_{1} 、 B_{2} 、 B_{3} 、 B_{4} 、 ⋯ ⋯ 、 B_{2022}$ 在y轴的正半轴上， $△ O A_{1} B_{1} 、 △ B_{1} A_{2} B_{2} 、 ⋯ ⋯ 、 △ B_{2021} A_{2022} B_{2022}$ 都是等腰直角三角形，则 $B_{2021} A_{2022} =$ ．

查看试题解析

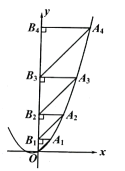
四、解答题

17. 河南省对居民生活用电采用阶梯电价，鼓励居民节约用电，其中年用电量为2160千瓦时及以下执行基础电价0.56元/千瓦时；2160~3120千瓦时的部分按0.61元/千瓦时收费；超过3120千瓦时的部分按0.86元/千瓦时收费．为了解某小区居民生活用电情况．调查小组从该小区随机调查了200户居民的月平均用电量x（千瓦时），并将全部调查数据分组统计如下：
组别
$60 ＜ x \leq 100$
$100 ＜ x \leq 140$
$140 ＜ x \leq 180$
$180 ＜ x \leq 220$
$220 ＜ x \leq 260$
$260 ＜ x \leq 300$
频数（户数）
28
42
a
30
20
10
把这200个数据从小到大排列后，其中第96到第105（包含第96和第105这两个数据）个数据依次为：
148 148 150 152 152 154 160 161 161 162
根据以上信息，回答下列问题：

(1)、本次调查中，该小区居民月平均用电量的中位数为，上表a= ．

(2)、估计该小区能享受基础电价的居民占全小区的百分比．

(3)、国家在制订收费标准时，为了减轻居民用电负担，制订的收费标准能让85%的用户享受基础电价．请你根据以上信息对该小区居民的用电情况进行评价，并写出一条建议．

查看试题解析
18. 如图1的风力发电机，风轮的三个叶片均匀分布，当风轮的叶片在风力作用下旋转时，最高点距地面 $145 m$ ，最低点距地面 $55 m$ ．如图2是该风力发电机的示意图，发电机的塔身 $O D$ 垂直于水平地面 $M N$ （点 $O$ ， $A$ ， $B$ ， $C$ ， $D$ ， $M$ ， $N$ 在同一平面内）．

(1)、求风轮叶片 $O A$ 的长度；

(2)、如图2，点 $A$ 在 $O D$ 右侧，且 $α = 14.4 °$ ．求此时风叶 $O B$ 的端点 $B$ 距地面的高度．（参考数据： $s i n 44.4 ° \approx 0.70$ ， $t a n 44.4 ° \approx 0.98$ ）

查看试题解析
19. 无锡水蜜桃享誉海内外，老王用3000元购进了一批水蜜桃.第一天，很快以比进价高40% 的价格卖出150千克.第二天，他发现剩余的水蜜桃卖相已不太好，于是果断地以比进价低20%的价格将剩余的水蜜桃全部售出，本次生意老王一共获利750元.

(1)、求这批水蜜桃进价为多少元？

(2)、老王用3000元按第一次的价格又购进了一批水蜜桃.第一天同样以比进价高40% 的价格卖出150千克，第二天，老王把卖相不好的水蜜桃挑出，单独打折销售，售价为10元/千克，结果很快被一抢而空，其余的仍按第一天的价格销售，且当天全部售完.若老王这次至少获利1000元，请问打折销售的水蜜桃最多多少千克？（精确到1千克.）

查看试题解析
20. 如图，在 $Rt △ A B C$ 中， $∠ A C B = 90 °$ ， $⊙ O$ 与 $B C$ ， $A C$ 分别相切于点E，F， $B O$ 平分 $∠ A B C$ ，连接 $O A$ .

(1)、求证： $A B$ 是 $⊙ O$ 的切线；

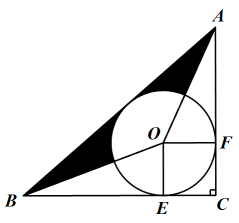(2)、若 $B E = A C = 3$ ， $⊙ O$ 的半径是1，求图中阴影部分的面积.

查看试题解析
21. “燃情冰雪，一起向未来”，北京冬奥会于2022年2月4日如约而至，某商家看准商机，进行冬奥会吉祥物“冰墩墩”纪念品的销售，每个纪念品进价40元．当销售单价定为46元时，每天可售出400个，由于销售火爆，商家决定提价销售．经市场调研发现，销售单价每上涨1元，每天销量减少10个，且规定利润率不得高于50%．设每天销售量为y个，销售单价为x元．

(1)、求当每个纪念品的销售单价是多少元时，商家每天获利4800元；

(2)、将纪念品的销售单价定为多少元时，商家每天销售纪念品获得的利润w元最大？最大利润是多少元？

查看试题解析
22. 如图，四边形 $A B C D$ 的顶点坐标分别为 $A (0 ， \sqrt{3})$ ， $B (- \frac{1}{2} ， \frac{\sqrt{3}}{2})$ ， $C (1 ， 0)$ ， $D (1 ， \sqrt{3})$ ，抛物线经过 $A$ ， $B$ ， $D$ 三点．

(1)、求证：四边形 $A O C D$ 是矩形；

(2)、求抛物线的解析式；

(3)、 $△ A C D$ 绕平面内一点 $M$ 顺时针旋转 $90 °$ 得到 $△ A_{1} C_{1} D_{1}$ ，即点 $A$ ， $C$ ， $D$ 的对应点分别为 $A_{1}$ ， $C_{1}$ ， $D_{1}$ ，若 $△ A_{1} C_{1} D_{1}$ 恰好两个顶点落在抛物线上，请直接写出 $A_{1}$ 的坐标．

查看试题解析
23. 【问题情境】

(1)、如图1，在正方形ABCD中，E，F，G分别是BC，AB，CD上的点，FG⊥AE于点Q．求证：AE＝FG．

(2)、如图2，正方形网格中，点A，B，C，D为格点，AB交CD于点O．求tan∠AOC的值；

(3)、【拓展提升】
如图3，点P是线段AB上的动点，分别以AP，BP为边在AB的同侧作正方形APCD与正方形PBEF，连接DE分别交线段BC，PC于点M，N．
①求∠DMC的度数；
②连接AC交DE于点H，直接写出 $\frac{D H}{B C}$ 的值．

查看试题解析

组别	$60 ＜ x \leq 100$	$100 ＜ x \leq 140$	$140 ＜ x \leq 180$	$180 ＜ x \leq 220$	$220 ＜ x \leq 260$	$260 ＜ x \leq 300$
频数（户数）	28	42	a	30	20	10