山东省青岛市李沧区2022年九年级下学期二模考试数学试题
试卷更新日期:2022-07-13 类型:中考模拟
一、单选题
-
1. 下列品牌的标识中,是轴对称图形但不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. -5的绝对值是( )A、5 B、 C、 D、-53. 如图所示的正六棱柱的主视图是( )
2. -5的绝对值是( )A、5 B、 C、 D、-53. 如图所示的正六棱柱的主视图是( )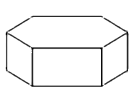 A、
A、 B、
B、 C、
C、 D、
D、 4. 月球与地球之间的平均距离约为38.4万公里,38.4万用科学记数法表示为( )A、 B、 C、 D、5. 在平面直角坐标系中,将线段平移后得到线段 , 点的对应点的坐标为 , 则点的对应点的坐标为( )A、 B、 C、 D、6. 下列运算中,正确的是( )A、 B、 C、 D、7. 如图,在中, , 以的中点为圆心,的长为半径作圆,交于点 , 则图中阴影部分的面积为( )
4. 月球与地球之间的平均距离约为38.4万公里,38.4万用科学记数法表示为( )A、 B、 C、 D、5. 在平面直角坐标系中,将线段平移后得到线段 , 点的对应点的坐标为 , 则点的对应点的坐标为( )A、 B、 C、 D、6. 下列运算中,正确的是( )A、 B、 C、 D、7. 如图,在中, , 以的中点为圆心,的长为半径作圆,交于点 , 则图中阴影部分的面积为( ) A、 B、 C、 D、8. 已知二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+c的图象和反比例函数y= 的图象在同一坐标系中大致为( )
A、 B、 C、 D、8. 已知二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+c的图象和反比例函数y= 的图象在同一坐标系中大致为( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
9. 计算: .10. 在一个不透明的袋中装有若干个红球,为了估计袋中红球的个数,小明在袋中放入3个黑球(每个球除颜色外其余都与红球相同),摇匀后每次随机从袋中摸出一个球,记下颜色后放回袋中,通过大量重复摸球试验后发现,摸到红球的频率稳定在0.85左右,则袋中红球约有个.11. 如图,正三角形的边与正五边形的一条边重合,则的度数为 .
 12. 写出一个具有性质①②的函数 . ①当时,;②当时,的值随值的增大而在增大.13. 如图,在中, , 将绕点顺时针旋转90°得到 , 为线段上的动点,以为圆心、为半径作⊙ , 当⊙与的边相切时,⊙的半径的长为 .
12. 写出一个具有性质①②的函数 . ①当时,;②当时,的值随值的增大而在增大.13. 如图,在中, , 将绕点顺时针旋转90°得到 , 为线段上的动点,以为圆心、为半径作⊙ , 当⊙与的边相切时,⊙的半径的长为 . 14. 如图,将一条长度为1的线段三等分,然后取走其中的一份,称为第一次操作;再将余下的每一条线段三等分,然后取走其中一份,称为第二次操作;…如此重复操作,当第n次操作结束时,被取走的所有线段长度之和为 .
14. 如图,将一条长度为1的线段三等分,然后取走其中的一份,称为第一次操作;再将余下的每一条线段三等分,然后取走其中一份,称为第二次操作;…如此重复操作,当第n次操作结束时,被取走的所有线段长度之和为 .
三、解答题
-
15. 如图,已知直线 , 直线分别与交于点 . 在线段上求作一点A,使点A到a,b的距离相等.
 16.(1)、解不等式组:(2)、计算:17. 在一次数学兴趣小组活动中,小红和小明两位同学设计了如图所示的两个转盘做游戏(每个转盘被分成面积相等的几个扇形,并在每个扇形区域内标上数学).游戏规则如下:两人分别同时转动甲、乙转盘,转盘停止后,若指针所指区域内两数和小于12,则小红获胜;若指针所指区域内两数和等于12,则为平局;若指针所指区域内两数和大于12,则小明获胜(若指针停在等分线上,重转一次,直到指针指向某一份内为止).
16.(1)、解不等式组:(2)、计算:17. 在一次数学兴趣小组活动中,小红和小明两位同学设计了如图所示的两个转盘做游戏(每个转盘被分成面积相等的几个扇形,并在每个扇形区域内标上数学).游戏规则如下:两人分别同时转动甲、乙转盘,转盘停止后,若指针所指区域内两数和小于12,则小红获胜;若指针所指区域内两数和等于12,则为平局;若指针所指区域内两数和大于12,则小明获胜(若指针停在等分线上,重转一次,直到指针指向某一份内为止). (1)、请用列表或画树状图的方法表示出上述游戏中两数和的所有可能的结果;(2)、求出小红获胜的概率.18. 一酒精消毒瓶如图1,为喷嘴,为按压柄,为伸缩连杆,和为导管,其示意图如图2, , , . 求点到直线的距离(结果精确到).(参考数据:)
(1)、请用列表或画树状图的方法表示出上述游戏中两数和的所有可能的结果;(2)、求出小红获胜的概率.18. 一酒精消毒瓶如图1,为喷嘴,为按压柄,为伸缩连杆,和为导管,其示意图如图2, , , . 求点到直线的距离(结果精确到).(参考数据:) 19. 为了提高农副产品的国际竞争力,我国一些行业协会对农副产品的规格进行了划分、某外贸公司要出口一批规格为 的鸡腿,现有两个厂家提供货源,它们的价格相同,鸡腿的品质相近质检员分别从两厂的产品中抽样调查了20只鸡腿,它们的质量(单位: )如下:
19. 为了提高农副产品的国际竞争力,我国一些行业协会对农副产品的规格进行了划分、某外贸公司要出口一批规格为 的鸡腿,现有两个厂家提供货源,它们的价格相同,鸡腿的品质相近质检员分别从两厂的产品中抽样调查了20只鸡腿,它们的质量(单位: )如下:甲厂:76,74,74,76,73,76,76,77,78,74,76,70,76,76,73,70,77,79,78,71;
甲厂鸡腿质量频数统计表
质量 ( )
频数
频率
2
0.1
3
0.15
10
5
0.25
合计
20
1
乙厂:75,76,77,77,78,77,76,71,74,75,79,71,72,74,73,74,70,79,75,77;
乙厂鸡腿质量频数分布直方图

分析上述数据,得到下表:
统计量
厂家
平均数
中位数
众数
方差
甲厂
75
76
6.3
乙厂
75
75
77
6.6
请你根据图表中的信息完成下列问题:
(1)、 , ;(2)、补全频数分布直方图;(3)、如果只考虑出口鸡腿规格,请结合表中的某个统计量,为外贸公司选购鸡腿提供参考建议;(4)、某外贸公司从甲厂采购了20000只鸡腿,并将质量(单位: )在 的鸡腿加工成优等品,请估计可以加工成优等品的鸡腿有多少只?20. 为了促进学生加强体育锻炼,增强体质,某中学从去年开始,开展了“足球训练营”活动,去年学校在某体育用品店购买品牌足球共花费3600元,品牌足球共花费2700元,且购买品牌足球数量是品牌数量的1.5倍,每个足球的售价,品牌比品牌便宜10元.(1)、去年品牌足球的销售单价各是多少元?(2)、今年由于参加“足球训练营”人数增加,需要从该店再购买两种足球共38个,已知该店对每个足球的售价,今年进行了调整,品牌去年提高了10%,品牌比去年降低了10%,如果今年购买两种足球的总费用不超过去年总费用的一半,那么学校最多可购买多少个品牌足球?21. 如图 (1)、在①;②;③这三个条件中任选一个补充在下面横线上,并完成解答要求.已知:如图,四边形为平行四边形,对角线相交于点 , 点在同一直线上, . (填写序号)(2)、求证:;(3)、若 , 判断四边形的形状,并证明你的结论.22. 如图1,排球场长为18m , 宽为9m , 网高为2.24m . 队员站在底线O点处发球,球从点O的正上方1.9m的C点发出,运动路线是抛物线的一部分,当球运动到最高点A时,高度为2.88m . 即BA=2.88m . 这时水平距离OB=7m , 以直线OB为x轴,直线OC为y轴,建立平面直角坐标系,如图2.
(1)、在①;②;③这三个条件中任选一个补充在下面横线上,并完成解答要求.已知:如图,四边形为平行四边形,对角线相交于点 , 点在同一直线上, . (填写序号)(2)、求证:;(3)、若 , 判断四边形的形状,并证明你的结论.22. 如图1,排球场长为18m , 宽为9m , 网高为2.24m . 队员站在底线O点处发球,球从点O的正上方1.9m的C点发出,运动路线是抛物线的一部分,当球运动到最高点A时,高度为2.88m . 即BA=2.88m . 这时水平距离OB=7m , 以直线OB为x轴,直线OC为y轴,建立平面直角坐标系,如图2. (1)、若球向正前方运动(即x轴垂直于底线),求球运动的高度y(m)与水平距离x(m)之间的函数关系式(不必写出x取值范围).并判断这次发球能否过网?是否出界?说明理由;(2)、若球过网后的落点是对方场地①号位内的点P(如图1,点P距底线1m , 边线0.5m),问发球点O在底线上的哪个位置?(参考数据: 取1.4)23. 【阅读理解】数形结合是解决数学问题的一种重要的思想方法,借助这种方法可将抽象的数学知识变得直观起来并且具有可操作性,从而可以帮助我们进行推理,获得结论.初中数学里的一些代数公式,很多都可以借助几何图形进行直观推导和解释.例如:求1+2+3+4+…+的值(其中是正整数).如果采用数形结合的方法,即用图形的性质来说明数量关系的事实,那就非常的直观.现利用图形的性质来求1+2+3+4+…+的值,方案如下:如图1,斜线左边的三角形图案是由上到下每层依次分别为1,2,3,…,个小圆圈排列组成的.而组成整个三角形小圆圈的个数恰为所求式子1+2+3+4+…+的值.为求式子的值,现把左边三角形倒放于斜线右边,与原三角形组成一个平行四边形.此时,组成平行四边形的小圆圈共有行,每行有个小圆圈,所以组成平行四边形小圆圈的总个数为个,因此,组成一个三角形小圆圈的个数为 , 即 .
(1)、若球向正前方运动(即x轴垂直于底线),求球运动的高度y(m)与水平距离x(m)之间的函数关系式(不必写出x取值范围).并判断这次发球能否过网?是否出界?说明理由;(2)、若球过网后的落点是对方场地①号位内的点P(如图1,点P距底线1m , 边线0.5m),问发球点O在底线上的哪个位置?(参考数据: 取1.4)23. 【阅读理解】数形结合是解决数学问题的一种重要的思想方法,借助这种方法可将抽象的数学知识变得直观起来并且具有可操作性,从而可以帮助我们进行推理,获得结论.初中数学里的一些代数公式,很多都可以借助几何图形进行直观推导和解释.例如:求1+2+3+4+…+的值(其中是正整数).如果采用数形结合的方法,即用图形的性质来说明数量关系的事实,那就非常的直观.现利用图形的性质来求1+2+3+4+…+的值,方案如下:如图1,斜线左边的三角形图案是由上到下每层依次分别为1,2,3,…,个小圆圈排列组成的.而组成整个三角形小圆圈的个数恰为所求式子1+2+3+4+…+的值.为求式子的值,现把左边三角形倒放于斜线右边,与原三角形组成一个平行四边形.此时,组成平行四边形的小圆圈共有行,每行有个小圆圈,所以组成平行四边形小圆圈的总个数为个,因此,组成一个三角形小圆圈的个数为 , 即 .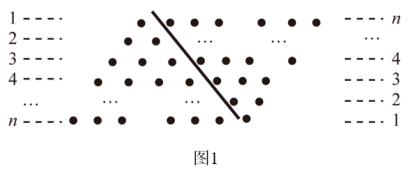
【问题提出】求的值(其中是正整数).
【问题解决】为解决上述问题,我们借鉴已有的经验,采用由特殊到一般,归纳的研究方法,利用数形结合法,借助图形进行推理获得结论.
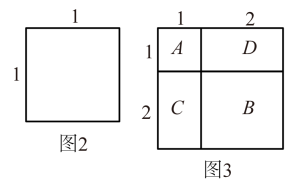
探究1:如图2,可以看成1个的正方形的面积,即
探究2:如图3,表示1个的正方形,其面积为:;表示1个的正方形,其面积为:;分别表示1个的长方形,其面积的和为:;的面积和为 , 而恰好可以拼成一个的大正方形.由此可得: .
(1)、探究3:请你类比上述探究过程,借助图形探究: ▲ = ▲ . (要求自己构造图形并写出推证过程)(2)、【结论归纳】将上述探究过程发现的规律,推广到一般情况中去,通过归纳,我们便可以得到:=(要求直接写出结论,不必写出推证过程)(3)、【结论应用】图4是由若干个棱长为1的小正方体搭成的大正方体,图中大小正方体一共有多少个?为了准确数出大小正方体的总个数,我们可以分类统计,即数出棱长分别是1,2,3,4,5,6的正方体的个数,再求总和.例如:棱长是1的正方体有:个,
棱长是2的正方体有:个,
……
棱长是6的正方体有:个;
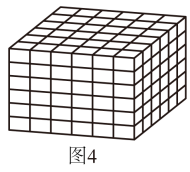
然后利用上面归纳的结论,通过计算,可得图4中大小正方体的个数为 .
(4)、【逆向应用】如果由若干个棱长为1的小正方体搭成的大正方体中,大小正方体一共有36100个,那么棱长为1的小正方体的个数为 .(5)、【拓展探究】观察下列各式:
若(为正整数)按上面规律展开后,发现等式右边含有“2021”这个数,则的值 .
24. 已知:线段和矩形如图①摆放(点与点重合),点在边上, . 如图②,从图①的位置出发,沿方向运动,速度为;动点同时从点出发,沿方向运动,速度为 . 点为的中点,连接与相交于点 , 设运动时间为 . 解答下列问题: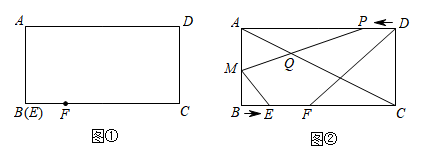 (1)、当时,求的值;(2)、设五边形的面积为 , 求与的关系式;(3)、当时,求线段的长;(4)、当为何值时,五边形的周长最小,最小是多少?(直接写出答案即可)
(1)、当时,求的值;(2)、设五边形的面积为 , 求与的关系式;(3)、当时,求线段的长;(4)、当为何值时,五边形的周长最小,最小是多少?(直接写出答案即可)