山东省青岛市崂山区2022年中考二模数学试题
试卷更新日期:2022-07-13 类型:中考模拟
一、单选题
-
1. 下列四个图形中,轴对称图形是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图是由6个同样大小的正方体摆成的几何体.将正方体①移走后,所得几何体( )
2. 如图是由6个同样大小的正方体摆成的几何体.将正方体①移走后,所得几何体( )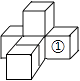 A、主视图改变,左视图改变 B、俯视图不变,左视图不变 C、俯视图改变,左视图改变 D、主视图改变,左视图不变3. 石墨烯具有优异的光学、电学、力学特性,在材料学、微纳加工、能源、生物医学和药物传递等方面具有重要的应用前景,被认为是一种未来革命性的材料,石墨烯中每两个相邻碳原子间的键长为0.000000000142米 ,数字“0.000000000142”用科学记数法表示为( )A、 B、 C、 D、4. 实数 , 在数轴上对应点的位置如图所示,下列结论正确的是( )
A、主视图改变,左视图改变 B、俯视图不变,左视图不变 C、俯视图改变,左视图改变 D、主视图改变,左视图不变3. 石墨烯具有优异的光学、电学、力学特性,在材料学、微纳加工、能源、生物医学和药物传递等方面具有重要的应用前景,被认为是一种未来革命性的材料,石墨烯中每两个相邻碳原子间的键长为0.000000000142米 ,数字“0.000000000142”用科学记数法表示为( )A、 B、 C、 D、4. 实数 , 在数轴上对应点的位置如图所示,下列结论正确的是( ) A、 B、 C、 D、5. 下面运算正确的是( )A、 B、 C、 D、6. 如图,将线段绕原点按逆时针方向旋转 , 得到线段 , 则点的坐标是( )
A、 B、 C、 D、5. 下面运算正确的是( )A、 B、 C、 D、6. 如图,将线段绕原点按逆时针方向旋转 , 得到线段 , 则点的坐标是( ) A、(1,) B、( , ) C、(3,) D、( , 3)7. 如图,五边形是⊙O的内接正五边形,则的度数为( )
A、(1,) B、( , ) C、(3,) D、( , 3)7. 如图,五边形是⊙O的内接正五边形,则的度数为( ) A、 B、 C、 D、8. 已知一次函数的图像如图所示,则二次函数和反比例函数在同一坐标系内的图象可能是( )
A、 B、 C、 D、8. 已知一次函数的图像如图所示,则二次函数和反比例函数在同一坐标系内的图象可能是( )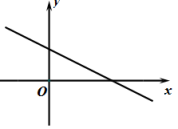 A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
9. 计算: .10. 为调查落实“双减”政策效果,某班级随机调查了10名学生一周平均每天的睡眠时间,统计结果如下表,则这些被调查学生的平均睡眠时间为小时.
时间/小时
7
8
9
10
11
人数/人
1
2
2
3
2
11. 关于的一元二次方程有两个相等的实数根,则值为 .12. 端午节是我国入选世界非物质文化遗产的传统节日,端午节吃粽子是中华民族的传统习俗.某公司计划制作48盒粽子送给福利院,为了尽快让福利院拿到粽子,在实际加工过程中加快了制作速度,平均每天多制作了6盒,因此提前4天完成任务,设原计划x天完成,那么根据题意可以列出的方程为: .13. 如图,在中,为圆心,为直径,为圆上一点, , , 则阴影部分面积为; 14. 如图,在等边中, , , , 分别为边 , 上的点,将沿所在直线翻折,点落在点,得到三角形 , 则的面积为 .
14. 如图,在等边中, , , , 分别为边 , 上的点,将沿所在直线翻折,点落在点,得到三角形 , 则的面积为 .
三、解答题
-
15. 已知:线段a.

求作:等腰直角 , 使得斜边 .
16. 计算及解不等式组:(1)、;(2)、并写出它的正整数解.17. 小明与小刚做游戏,在甲、乙两个不透明的口袋中,分别装有除标号外完全相同的小球,其中甲口袋中的3个小球上分别标有数字1,2,3,乙口袋中的4个小球上分别标有数字1,2,3,4,先从甲袋中随机摸出一个小球,记录数字为 , 再从乙袋中随机摸出一个小球,记录数字为 . 如果则小刚获胜,否则小明获胜,游戏公平吗?请说明理由.18. 如图,为了测量灯塔的高度,小明在点处测得灯塔顶端点的仰角为 , 然后他沿着坡角为斜坡前进米到达点 , 再沿水平方向走米到达了灯塔底端点 , 点 , , , , 在同一平面中, , . 求旗杆的高度.(参考数据: , , )
 19. 贯彻国家的“双减政策”,某校调查关于“初中书面作业平均完成时间不超过90分钟”的落实情况,随机调查了该校部分学生,根据调查结果绘制成如下统计图表.
19. 贯彻国家的“双减政策”,某校调查关于“初中书面作业平均完成时间不超过90分钟”的落实情况,随机调查了该校部分学生,根据调查结果绘制成如下统计图表.每天作业完成时间情况频数分布表:
组别
每天作业完成时间分钟
人数
A
a
B
35
C
c
D
10

请根据以上图表信息,解答下列问题:
(1)、求 , , 的值;(2)、若该校约有950名学生,请估计书面作业平均完成时间低于90分钟的学生人数.20. 如图,一次函数图象与反比例函数图象相交于 , 两点. (1)、求 , 的值;(2)、根据图象直接写出满足的的取值范围.21. 如图,在中,点 , 分别为 , 的中点,连接 , .
(1)、求 , 的值;(2)、根据图象直接写出满足的的取值范围.21. 如图,在中,点 , 分别为 , 的中点,连接 , . (1)、求证:;(2)、当 , 时,四边形是什么特殊四边形?请说明理由.22. 小敏在今年的校运动会跳远比赛中跳出了满意一跳,如图一所示,小敏重心高度(m)与时间(s)之间的关系式为 , 小敏重心高度(m)与水平距离(m)之间的函数图象为如图二所示抛物线,点B与点A纵坐标相等,点 , 的水平距离为5m,点为重心最高点.
(1)、求证:;(2)、当 , 时,四边形是什么特殊四边形?请说明理由.22. 小敏在今年的校运动会跳远比赛中跳出了满意一跳,如图一所示,小敏重心高度(m)与时间(s)之间的关系式为 , 小敏重心高度(m)与水平距离(m)之间的函数图象为如图二所示抛物线,点B与点A纵坐标相等,点 , 的水平距离为5m,点为重心最高点. (1)、小敏起跳后几秒重心到达最大高度? 最大高度为多少?(2)、求小敏重心高度(m)与水平距离(m)之间的关系式(无需考虑自变量的取值范围).23. 实际问题:
(1)、小敏起跳后几秒重心到达最大高度? 最大高度为多少?(2)、求小敏重心高度(m)与水平距离(m)之间的关系式(无需考虑自变量的取值范围).23. 实际问题:婚礼上有116名宾客,地面上水平放置了一个长方体蛋糕,要保证这116名宾客都能分得蛋糕(忽略大小,水平切割的方向只能与地面平行,垂直切割只能与地面垂直),小明说我10刀即可完成任务,你认为小明是怎样切这个蛋糕才能完成任务.
问题探究:
为解决这个问题我们从最简单的长方形分割开始研究.
探究一:用一条直线分一个长方形,最多可以分成几部分?
如图1所示,一条线来分多出1部分,最多分成1+1=2部分;

探究二:用2条直线分一个长方形,最多可以分成几部分?
如图2所示,第2条线与第一条线相交,多出2部分,最多分成1+1+2=4部分;
探究三:用3条直线分一个长方形,最多可以分成几部分?
如图3所示,第3条线与前2条线相交,多出3部分,最多分成1+1+2+3=7部分;
探究四:用4条直线分一个长方形,最多可以分成几部分?
如图4所示,第4条线与原来3条线相交, 多出4部分,最多分1+1+2+3+4=11部分;
(1)、探究五:用5条直线分一个长方形,第5条线与原来4条线相交,多出部分,即最多分成部分;(2)、探究六:用条直线分一个长方形,最多可以分成部分;(用含的代数式表示)(3)、探究七:我们可以将开始提出的问题转化为切割长方体,借助以上探究长方形切割的结论如何将长方体切割成14块?我们只需要在探究三的基础上,先在长方体中竖直切割3刀最多分成7块,平行于地面切一刀,此时4刀可切成7×2=14块.
探究八:如何用最少的切割次数,将一个长方体蛋糕切割成44块,请说明切割过程,无需画图;
问题解决:
(4)、婚礼上有116名宾客,地面上放了一个长方体蛋糕,要保证这116名宾客都能分得蛋糕(忽略大小,水平切割的方向只能与地面平行,垂直切割只能与地面垂直),小明说我10刀即可完成任务,你认为小明是怎样切这个蛋糕?请说明切割的过程,无需画图.24. 已知:如图,在中, , cm,cm,为边上的高,点从点出发,沿方向匀速运动,速度为cm/s;同时,点从点出发,沿方向匀速运动,速度为cm/s.设运动时间为 .解答下列问题:
 (1)、当为何值时,;(2)、当中点在上时,求的值;(3)、设四边形的面积为 , 求与的函数关系式,并求最小值;(4)、是否存在某一时刻 , 使得 , 若存在,求出的值;若不存在,请说明理由.
(1)、当为何值时,;(2)、当中点在上时,求的值;(3)、设四边形的面积为 , 求与的函数关系式,并求最小值;(4)、是否存在某一时刻 , 使得 , 若存在,求出的值;若不存在,请说明理由.