山东省济南市商河县2022年中考一模数学试题
试卷更新日期:2022-07-13 类型:中考模拟
一、单选题
-
1. 下列各数中,比-2小的数是( ).A、-3 B、-1 C、0 D、12. 如图所示的物体,从正面看到的平面图形是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 目前,商河县西部新城长青河绿轴带绿化工程正在进行,整个工程预计栽种绿植16000株.16000用科学记数法可表示为( )A、 B、 C、 D、4. 如图,把一块含45°角的直角三角板的直角顶点放在直尺的一边上,如果∠1=33°,那么∠2为( )
3. 目前,商河县西部新城长青河绿轴带绿化工程正在进行,整个工程预计栽种绿植16000株.16000用科学记数法可表示为( )A、 B、 C、 D、4. 如图,把一块含45°角的直角三角板的直角顶点放在直尺的一边上,如果∠1=33°,那么∠2为( ) A、33° B、57° C、67° D、60°5. 下列图形中既是轴对称图形又是中心对称图形的是( )A、
A、33° B、57° C、67° D、60°5. 下列图形中既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 6. 小军为了了解本校运动员百米短跑所用步数的情况,对校运会中百米短跑决赛的8名男运动员的步数进行了统计,记录的数据如下:67、66、67、68、67、69、68、71,这组数据的众数和极差分别为( )A、67 4 B、67 5 C、68 4 D、68 57. 下列计算正确的是( )A、 B、 C、 D、8. 如图,菱形中,对角线相交于点O,E为边中点,菱形的周长为28,则的长等于( )
6. 小军为了了解本校运动员百米短跑所用步数的情况,对校运会中百米短跑决赛的8名男运动员的步数进行了统计,记录的数据如下:67、66、67、68、67、69、68、71,这组数据的众数和极差分别为( )A、67 4 B、67 5 C、68 4 D、68 57. 下列计算正确的是( )A、 B、 C、 D、8. 如图,菱形中,对角线相交于点O,E为边中点,菱形的周长为28,则的长等于( )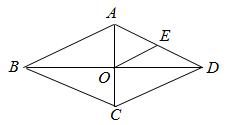 A、3.5 B、4 C、7 D、149. 已知一次函数中y随x的增大而减小,且 , 则在直角坐标系内它的大致图象是( )A、
A、3.5 B、4 C、7 D、149. 已知一次函数中y随x的增大而减小,且 , 则在直角坐标系内它的大致图象是( )A、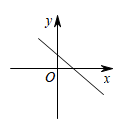 B、
B、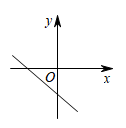 C、
C、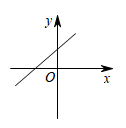 D、
D、 10. 如图,已知平行四边形AOBC的顶点O(0,0),A(−1,2);点B在x轴正半轴上,按以下步骤作图:
10. 如图,已知平行四边形AOBC的顶点O(0,0),A(−1,2);点B在x轴正半轴上,按以下步骤作图:①以点O为圆心,适当长度为半径作弧,分别交边OA,OB于点D,E;②分别以点D,E为圆心,大于DE的长为半径作弧,两弧在∠AOB内交于点F;③作射线OF,交边AC于点G,则点G的坐标为( )
 A、 B、 C、 D、11. 如图,为测量学校旗杆AB的高度,小明从旗杆正前方3米处的点C出发,沿坡度为的斜坡CD前进米到达点D,在点D处放置测角仪,测得旗杆顶部A的仰角为37°,量得测角仪DE的高为1.5米,A、B、C、D、E在同一平面内,且旗杆和测角仪都与地面垂直,则旗杆AB的高度为( )(精确到0.1).(参考数据: , , , )
A、 B、 C、 D、11. 如图,为测量学校旗杆AB的高度,小明从旗杆正前方3米处的点C出发,沿坡度为的斜坡CD前进米到达点D,在点D处放置测角仪,测得旗杆顶部A的仰角为37°,量得测角仪DE的高为1.5米,A、B、C、D、E在同一平面内,且旗杆和测角仪都与地面垂直,则旗杆AB的高度为( )(精确到0.1).(参考数据: , , , ) A、6.7 B、7.7 C、8.7 D、8.512. 在平面直角坐标系中,已知,点A(1,m)和点B(3,n)(其中mn<0)在抛物线y=ax2+bx(a>0)上.若点(−1,y1),(2,y2),(4,y3)也在该抛物线上,则y1 , y2 , y3的大小关系是( )A、 B、 C、 D、
A、6.7 B、7.7 C、8.7 D、8.512. 在平面直角坐标系中,已知,点A(1,m)和点B(3,n)(其中mn<0)在抛物线y=ax2+bx(a>0)上.若点(−1,y1),(2,y2),(4,y3)也在该抛物线上,则y1 , y2 , y3的大小关系是( )A、 B、 C、 D、二、填空题
-
13. 分解因式: .14. 从1、2、3中任取一个数作为十位上的数字,再从余下的数字中任取一个数作为个位上的数字,那么组成的两位数是4的倍数的概率是15. 设 是方程 的两个根,则 .
16. 如图,将边长为3的正六边形铁丝框ABCDEF变形为以点A为圆心,AB为半径的扇形(忽略铁丝的粗细).则所得扇形AFB(阴影部分)的面积为 .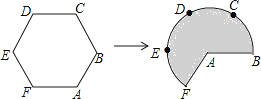 17. 一次越野跑中,当小明跑了1600米时,小刚跑了1400米,小明、小刚在此后所跑的路程y(米)与时间t(秒)之间的函数关系如图所示,则这次越野跑的全程为米.
17. 一次越野跑中,当小明跑了1600米时,小刚跑了1400米,小明、小刚在此后所跑的路程y(米)与时间t(秒)之间的函数关系如图所示,则这次越野跑的全程为米. 18. 如图,在矩形ABCD中,AB=9,点E,F分别在BC,CD上,将△ABE沿AE折叠,使点B落在AC上的点B′处,又将△CEF沿EF折叠,使点C落在直线EB′与AD的交点C′处,则DF的值为 .
18. 如图,在矩形ABCD中,AB=9,点E,F分别在BC,CD上,将△ABE沿AE折叠,使点B落在AC上的点B′处,又将△CEF沿EF折叠,使点C落在直线EB′与AD的交点C′处,则DF的值为 .
三、解答题
-
19. 计算:20. 解不等式组:并写出它的所有整数解.21. 如图,在▱ABCD中,点E是AB边的中点,DE的延长线与CB的延长线交于点F.
求证:BC=BF.
 22. 随机抽取该校男生、女生进行抽样调查.已知抽取的样本中,男生、女生的人数相同,利用所得数据绘制如下统计图表:
22. 随机抽取该校男生、女生进行抽样调查.已知抽取的样本中,男生、女生的人数相同,利用所得数据绘制如下统计图表:组别
身高/cm
A
B
C
D
E

根据图表提供的信息,回答下列问题:
(1)、样本中,女生身高在E组的有2人,抽样调查了名女生;(2)、补全条形统计图;(3)、样本中,男生的身高中位数在组;(4)、已知该校共有男生400人,女生380人,请估计身高在之间的学生约有人.23. 如图,AB是⊙O的弦,D为半径OA上一点,过D作交弦AB于点E,交⊙O于点F,BC是⊙O的切线.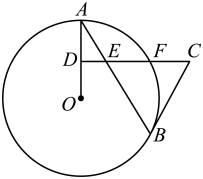 (1)、求证:;(2)、如果 , , , 求⊙O的半径.24. 有大小两种货车,3辆大货车与4辆小货车一次可以运货18吨,2辆大货车与6辆小货车一次可以运货17吨.(1)、请问1辆大货车和1辆小货车一次可以分别运货多少吨?(2)、目前有33吨货物需要运输,货运公司拟安排大小货车共计10辆,全部货物一次运完.其中每辆大货车一次运货花费130元,每辆小货车一次运货花费100元,请问货运公司应如何安排车辆最节省费用?最省费用是多少?25. 如图,在平面直角坐标系xOy中,点A(a,﹣ )在直线y=﹣ 上,AB∥y轴,且点B的纵坐标为1,双曲线y= 经过点B.
(1)、求证:;(2)、如果 , , , 求⊙O的半径.24. 有大小两种货车,3辆大货车与4辆小货车一次可以运货18吨,2辆大货车与6辆小货车一次可以运货17吨.(1)、请问1辆大货车和1辆小货车一次可以分别运货多少吨?(2)、目前有33吨货物需要运输,货运公司拟安排大小货车共计10辆,全部货物一次运完.其中每辆大货车一次运货花费130元,每辆小货车一次运货花费100元,请问货运公司应如何安排车辆最节省费用?最省费用是多少?25. 如图,在平面直角坐标系xOy中,点A(a,﹣ )在直线y=﹣ 上,AB∥y轴,且点B的纵坐标为1,双曲线y= 经过点B. (1)、求a的值及双曲线y= 的解析式;(2)、经过点B的直线与双曲线y= 的另一个交点为点C,且△ABC的面积为 .
(1)、求a的值及双曲线y= 的解析式;(2)、经过点B的直线与双曲线y= 的另一个交点为点C,且△ABC的面积为 .①求直线BC的解析式;
②过点B作BD∥x轴交直线y=﹣ 于点D,点P是直线BC上的一个动点.若将△BDP以它的一边为对称轴进行翻折,翻折前后的两个三角形所组成的四边形为正方形,直接写出所有满足条件的点P的坐标.
26. 在△ABC和△ADE中,BA=BC,DA=DE,且∠ABC=∠ADE,点E在△ABC的内部,连接EC,EB和ED,设EC=k•BD(k≠0). (1)、当∠ABC=∠ADE=60°时,如图1,请求出k值,并给予证明;(2)、当∠ABC=∠ADE=90°时:
(1)、当∠ABC=∠ADE=60°时,如图1,请求出k值,并给予证明;(2)、当∠ABC=∠ADE=90°时:①如图2,(1)中的k值是否发生变化,如无变化,请给予证明;如有变化,请求出k值并说明理由;
②如图3,当D,E,C三点共线,且E为DC中点时,请求出tan∠EAC的值.
27. 如图,抛物线y=ax2+2x−3与x轴交于A、B两点,且B(1,0).
 (1)、求抛物线的解析式和点A的坐标;(2)、如图1,点P是直线y=x上在x轴上方的动点,当直线y=x平分∠APB时,求点P的坐标;(3)、如图2,已知直线y=x−分别与x轴、y轴交于C、F两点,点Q是直线CF下方的抛物线上的一个动点,过点Q作y轴的平行线,交直线CF于点D,点E在线段CD的延长线上,连接QE.问:以QD为腰的等腰△QDE的面积是否存在最大值?若存在,请求出这个最大值;若不存在,请说明理由.
(1)、求抛物线的解析式和点A的坐标;(2)、如图1,点P是直线y=x上在x轴上方的动点,当直线y=x平分∠APB时,求点P的坐标;(3)、如图2,已知直线y=x−分别与x轴、y轴交于C、F两点,点Q是直线CF下方的抛物线上的一个动点,过点Q作y轴的平行线,交直线CF于点D,点E在线段CD的延长线上,连接QE.问:以QD为腰的等腰△QDE的面积是否存在最大值?若存在,请求出这个最大值;若不存在,请说明理由.