山东省济南市2022年九年级数学一模测试题

试卷更新日期：2022-07-13 类型：中考模拟

进入出卷网下载

一、单选题

1. 16的算术平方根是 $($ $)$

A、4 B、-4 C、±4 D、8

查看试题解析
2. 中国移动数据中心IDC项目近日在高新区正式开工建设，该项目规划建设规模12.6万平方米，建成后将成为山东省最大的数据业务中心．其中126000用科学记数法表示应为（）

A、1.26×10⁶ B、12.6×10⁴ C、0.126×10⁶ D、1.26×10⁵

查看试题解析
3.
从棱长为2a的正方体零件的一角，挖去一个棱长为a的小正方体，得到一个如图所示的零件，则这个零件的俯视图是（）

A、 B、 C、 D、

查看试题解析
4.
如图，直线m∥n，∠1=70°，∠2=30°，则∠A等于（）

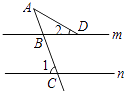A、30° B、35° C、40° D、50°

查看试题解析
5. 下面的图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
6. 下列计算中，正确的是（）

A、 $2 a + 3 b = 5 a b$ B、 ${(3 a^{3})}^{2} = 6 a^{6}$ C、 $a^{6} + a^{2} = a^{8}$ D、 $- 3 a + 2 a = - a$

查看试题解析
7. 化简 $\frac{a^{2} - b^{2}}{a b} - \frac{a b - b^{2}}{a b - a^{2}}$ 等于（）

A、 $\frac{b}{a}$ B、 $\frac{a}{b}$ C、﹣ $\frac{b}{a}$ D、﹣ $\frac{a}{b}$

查看试题解析
8. 某学校组织知识竞赛，共设20道题，其中有关中国优秀传统文化试题10道，实践应用题4道，创新能力题6道，小捷从中任选一道试题作答，他选中创新能力试题的概率是（）

A、 $\frac{1}{5}$ B、 $\frac{3}{10}$ C、 $\frac{2}{5}$ D、 $\frac{1}{2}$

查看试题解析
9. 已知反比例函数 $y = \frac{k}{x}$ ，当 $x < 0$ 时，y随x的增大而减小，那么一次的数 $y = - k x + k$ 的图像经过第（）

A、一，二，三象限 B、一，二，四象限 C、一，三，四象限 D、二，三，四象限

查看试题解析
10. 已知锐角 $∠ A O B = 40 °$ ，如图，按下列步骤作图：①在 $O A$ 边取一点D，以O为圆心， $O D$ 长为半径画 $\overset{⌢}{M N}$ ，交 $O B$ 于点C，连接 $C D$ .②以D为圆心， $D O$ 长为半径画 $\overset{⌢}{G H}$ ，交 $O B$ 于点E，连接 $D E$ .则 $∠ C D E$ 的度数为（）

A、 $20 °$ B、 $30 °$ C、 $40 °$ D、 $50 °$

查看试题解析
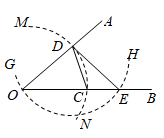11. 为践行“绿水青山就是金山银山”的重要思想，某森林保护区开展了寻找古树活动．如图，在一个坡度（或坡比） $i$ =1：2.4的山坡AB上发现有一棵占树CD．测得古树底端C到山脚点A的距离AC=26米，在距山脚点A水平距离6米的点E处，测得古树顶端D的仰角∠AED=48°（古树CD与山坡AB的剖面、点E在同一平面上，古树CD与直线AE垂直），则古树CD的高度约为（）（参考数据： $s i n 48$ °≈0.73，cos8°≈0.67，tan48°≈1.11）

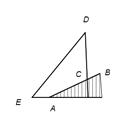A、17.0米 B、21.9米 C、23.3米 D、33.3米

查看试题解析
12. 已知函数y＝﹣x²+2ax，当x≤2时，函数值随x增大而增大，且对任意的1≤x₁≤a+1和1≤x₂≤a+1，x₁、x₂相应的函数值y₁、y₂总满足|y₁﹣y₂|≤16，则实数a的取值范围是（）

A、2≤a≤5 B、﹣3≤a≤5 C、a≥2 D、2≤a≤3

查看试题解析

二、填空题

13. 分解因式： $a^{3} - a =$ .

查看试题解析
14. 某校九年级（1）班40名同学中，14岁的有1人，15岁的有21人，16岁的有16人，17岁的有2人，则这个班同学年龄的中位数是岁．

查看试题解析
15. 如图，在正五边形ABCDE中，DM是边CD的延长线，连接BD，则∠BDM的度数是.

查看试题解析
16.
如图，将一块正方形空地划出部分区域进行绿化，原空地一边减少了2m，另一边减少了3m，剩余一块面积为20m²的矩形空地，则原正方形空地的边长为　 m．

查看试题解析
17. 一辆快车和一辆慢车将一批物资从甲地运往乙地，其中快车送达后立即沿原路返回，且往返速度的大小不变，两车离甲地的距离y（单位： $k m$ ）与慢车行驶时间t（单位：h）的函数关系如图，则两车先后两次相遇的间隔时间是h．

查看试题解析
18. 如图，在矩形纸片ABCD中，BC=4，E是BC的中点．将AB沿AE翻折，使点B落在AD边的B′处，AE为折痕，再将B′D沿B′G翻折，使点D恰好落在线段AC上的点F处，B′G为折痕，则tan∠FB′E= ．

查看试题解析

三、解答题

19. 计算： $| - \frac{1}{2} | + {(- 1)}^{2019} + 2 \sin 30 ° + {(\sqrt{3} - \sqrt{2})}^{0}$

查看试题解析
20. 解不等式组： ${\begin{array}{l} 3 x - 5 > 2 (x - 2) \\ \frac{x}{2} > x - 1 \end{array}$

查看试题解析
21. 如图，点 $E$ 和点 $F$ 分别在平行四边形 $A B C D$ 的边 $B C$ 和 $A D$ 上，线段 $E F$ 恰好经过 $B D$ 的中点 $O$ ．求证： $A F = C E$ ．

查看试题解析
22. 为应对新冠疫情，某药店到厂家选购A、B两种品牌的医用外科口罩，B品牌口罩每个进价比A品牌口罩每个进价多0.7元，若用7200元购进A品牌数量是用5000元购进B品牌数量的2倍．

(1)、求A、B两种品牌的口罩每个进价分别为多少元？

(2)、若A品牌口罩每个售价为2元，B品牌口罩每个售价为3元，药店老板决定一次性购进A、B两种品牌口罩共6000个，在这批口罩全部出售后所获利润不低于1800元．则最少购进B品牌口罩多少个？

查看试题解析
23. 如图，AB为⊙O的直径，C是⊙O上一点，D在AB的延长线上，且∠DCB=∠A．E是AB下半圆弧中点，连接CE交AD于F．

(1)、求证：CD与⊙O相切．

(2)、 AF=8，EF=2 $\sqrt{10}$ ，求⊙O的半径．

查看试题解析
24. 某社区为了调查居民第三季度的用电情况，随机抽取了小区20户居民的用电量进行调查．数据如下：（单位：度）
670，870，730，1140，700，690，1170，970，1000，970
730，840，1060，870，720，870，1060，930，840，870
整理数据：按如下分段整理样本数据并补至表格（表1）
用电量x（度）
$600 \leq x < 750$
$750 \leq x < 900$
$900 \leq x < 1050$
$1050 \leq x < 1200$
人数
a
⁶
b
⁴
分析数据：补全下列表格中的统计量（表2）
平均数
中位数
众数
885
c
d
得出结论：

(1)、表中的a= ， b= ， c= ， d= ．

(2)、若将表1中的数据制作成一个扇形统计图，则 $900 \leq x < 1050$ 所表示的扇形圆心角的度数为度．

(3)、如果该小区有住户400户，请根据样本估计用电量在 $600 \leq x < 900$ 的居民户数．

查看试题解析
25. 如图，在平面直角坐标系xOy中，一次函数y＝x+b的图象经过点C(0，2)，与反比例函数 $y = \frac{k}{x}$ （x＞0）的图象交于点A(1，a)．

(1)、求一次函数和反比例函数的表达式；

(2)、一次函数y＝x+b的图象与x轴交于B点，求 $△$ ABO的面积；

(3)、设M是反比例函数 $y = \frac{k}{x}$ （x＞0）图象上一点，N是直线AB上一点，若以点O、M、C、N为顶点的四边形是平行四边形，求点N的坐标．

查看试题解析
26. 在 $△ A B C$ 中，AB＝AC，M是平面内任意一点，将线段AM绕点A按顺时针方向旋转与∠BAC相等的角度，得到线段AN，连结NB．

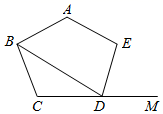
【感知】如图①，若M是线段BC上的任意一点，易证 $△ A B N ≌ △ A C M$ ，可知∠NAB＝∠MAC，BN＝MC．

(1)、【探究】如图②，点E是AB延长线上的点，若点M是∠CBE内部射线BD上任意一点，连接MC，【感知】中的结论是否仍然成立？若成立，请给予证明，若不成立，请说明理由．

(2)、【拓展】如图③，在 $△ D E F$ 中，DE＝8，∠DEF＝60°，∠EDF＝75°，P是EF上的任意点，连接DP，将DP绕点D按顺时针方向旋转75°，得到线段DQ，连接EQ，则EQ的最小值为．

查看试题解析
27. 已知顶点为A抛物线 $y = a (x - \frac{1}{2})^{2} - 2$ 经过点 $B (- \frac{3}{2} ， 2)$ ，点 $C (\frac{5}{2} ， 2)$ ．

(1)、求抛物线的解析式；

(2)、如图1，直线AB与x轴相交于点M，y轴相交于点E，抛物线与y轴相交于点F，在直线AB上有一点P，若∠OPM＝∠MAF，求△POE的面积；

(3)、如图2，点Q是折线A﹣B﹣C上一点，过点Q作QN∥y轴，过点E作EN∥x轴，直线QN与直线EN相交于点N，连接QE，将△QEN沿QE翻折得到△QEN₁ ，若点N₁落在x轴上，请直接写出Q点的坐标．

查看试题解析

用电量x（度）	$600 \leq x < 750$	$750 \leq x < 900$	$900 \leq x < 1050$	$1050 \leq x < 1200$
人数	a	⁶	b	⁴

平均数	中位数	众数
885	c	d