内蒙古包头市青山区2022年九年级下学期二模数学试题
试卷更新日期:2022-07-13 类型:中考模拟
一、单选题
-
1. 2022相反数的倒数是( )A、 B、2021 C、-2021 D、2. 新型冠状病毒的直径大约为0.000000125米,0.000000125用科学记数法表示为( )A、 B、 C、 D、3. 不等式组的解集在数轴上表示为( )A、
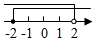 B、
B、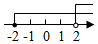 C、
C、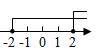 D、
D、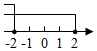 4. 某学习小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如下的表格,则符合这一结果的实验最有可能的是( )
4. 某学习小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如下的表格,则符合这一结果的实验最有可能的是( )实验次数
100
200
300
500
800
1000
2000
频率
0.365
0.328
0.330
0.334
0.336
0.332
0.333
A、一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃 B、在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀” C、抛一个质地均匀的正六面体骰子,向上的面点数是5 D、抛一枚硬币,出现反面的概率5. 下列计算正确的是( )A、 B、 C、 D、6. 如图是一物体的三视图,则这个几何体的侧面积为( ) A、 B、 C、 D、7. 如图,将一副三角板在平行四边形ABCD中作如下摆放,设 ,那么 ( )
A、 B、 C、 D、7. 如图,将一副三角板在平行四边形ABCD中作如下摆放,设 ,那么 ( )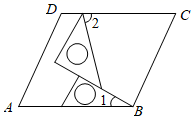 A、 B、 C、 D、8. 下列命题中,真命题的个数有( )
A、 B、 C、 D、8. 下列命题中,真命题的个数有( )①如果不等式的解集为 , 那么②已知二次函数 , 当时,y随x的增大而减小③顺次连接对角线相等的四边形的四边中点所形成的图形是菱形④各边对应成比例的两个多边形相似
A、1个 B、2个 C、3个 D、4个9. 如图,在菱形中,点分别是边的中点,连接 . 若菱形的面积为8,则的面积为( ) A、2 B、3 C、4 D、510. 已知二次函数y=x2+bx+c,当x>0时,函数的最小值为﹣3,当x≤0时,函数的最小值为﹣2,则b的值为( )A、6 B、2 C、﹣2 D、﹣311. 如图,△DEF的三个顶点分别在反比例函数xy=n与xy=m(x>0,m>n>0)的图象上,若DB⊥x轴于B点,FE⊥x轴于C点,若B为OC的中点,△DEF的面积为2,则m,n的关系式是( )
A、2 B、3 C、4 D、510. 已知二次函数y=x2+bx+c,当x>0时,函数的最小值为﹣3,当x≤0时,函数的最小值为﹣2,则b的值为( )A、6 B、2 C、﹣2 D、﹣311. 如图,△DEF的三个顶点分别在反比例函数xy=n与xy=m(x>0,m>n>0)的图象上,若DB⊥x轴于B点,FE⊥x轴于C点,若B为OC的中点,△DEF的面积为2,则m,n的关系式是( )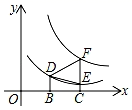 A、m﹣n=8 B、m+n=8 C、2m﹣n=8 D、2m+n=312. 已知:如图,为的直径,为的切线,D、B为切点,交于点E,的延长线交于点F,连接 . 以下结论:①;②点E为的内心;③;④ . 其中正确的只有( )
A、m﹣n=8 B、m+n=8 C、2m﹣n=8 D、2m+n=312. 已知:如图,为的直径,为的切线,D、B为切点,交于点E,的延长线交于点F,连接 . 以下结论:①;②点E为的内心;③;④ . 其中正确的只有( ) A、①② B、②③④ C、①③④ D、①②④
A、①② B、②③④ C、①③④ D、①②④二、填空题
-
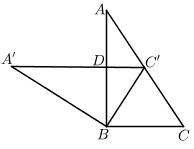
13. 因式分解: .14. 现有4条线段,长度依次是2、4、6、7,从中任选三条,能组成三角形的概率是 .15. 计算: .16. 两个全等的直角三角形完全重合在一起,把上面的一个直角三角形绕直角顶点B逆时针旋转度,转到的位置,若恰为AC的中点,则 .
 17. 甲、乙、丙三名同学观察完某个一次函数的图象,各叙述如下:
17. 甲、乙、丙三名同学观察完某个一次函数的图象,各叙述如下:甲:函数的图象经过点(0,1);
乙:y随x的增大而减小;
丙:函数的图象不经过第三象限.
根据他们的叙述,写出满足上述性质的一个函数表达式为 .
18. 六个带 角的直角三角板拼成一个正六边形,直角三角板的最短边为1,求中间正六边形的面积 .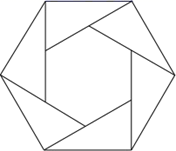 19. 若关于x的分式方程=有正整数解,则整数m为 .20. 如图,菱形ABCD的对角线AC,BD相交于点O,点P为AB边上一动点(不与点A,B重合),于点E,于点F,若 , , 则EF的最小值为 .
19. 若关于x的分式方程=有正整数解,则整数m为 .20. 如图,菱形ABCD的对角线AC,BD相交于点O,点P为AB边上一动点(不与点A,B重合),于点E,于点F,若 , , 则EF的最小值为 .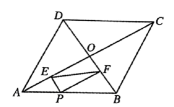
三、解答题
-
21. 为了解某市八年级数学期末考试情况,进行了抽样调查,过程如下,请将有关问题补充完整.
收集数据:随机抽取甲乙两所学校的各20名学生的数学成绩进行分析(满分为100分)
甲
91
89
77
86
71
31
97
93
72
91
81
92
85
85
95
88
88
90
44
91
乙
84
93
66
69
76
87
77
82
85
88
90
88
67
88
91
96
68
97
59
88
整理、描述数据:按如表数据段整理、描述这两组数据
分段学校
甲
1
1
0
0
3
7
8
乙
0
0
1
4
2
8
5
分析数据:两组数据的平均数、中位数、众数、方差如表
统计量学校
平均数
中位数
众数
方差
甲
81.85
a
b
268.43
乙
c
86
88
115.25
得出结论
(1)、经统计,表格中a=;b=;c=;(2)、若甲学校有600名八年级学生,估计这次考试成绩80分以上人数为;(3)、可以推断出学校学生的数学水平较高,理由为: .22. 图1是我国某型号隐形战斗机模型,全动型后掠翼垂尾是这款战斗机亮点之一,图2是垂尾模型的轴切面,并通过垂尾模型的外围测得如下数据, , , , , 且 , 求出垂尾模型的面积.(结果保留根号) 23. 2022年北京冬奥会吉祥物冰墩墩深受大家的喜欢.某商家两次购进冰墩墩进行销售,第一次用22000元,很快销售一空,第二次又用48000元购进同款冰墩墩,所购进数量是第一次的2倍,但单价贵了10元.(1)、求该商家第一次购进冰墩墩多少个?(2)、若所有冰墩墩都按相同的标价销售,要求全部销售完后的利润率不低于20%(不考虑其他因素),那么每个冰墩墩的标价至少为多少元?24. 如图,在 中, ,点O在 上, ,点D在 上,以点O为圆心, 为半径作圆,交 的延长线于点E , 交 于点F , .
23. 2022年北京冬奥会吉祥物冰墩墩深受大家的喜欢.某商家两次购进冰墩墩进行销售,第一次用22000元,很快销售一空,第二次又用48000元购进同款冰墩墩,所购进数量是第一次的2倍,但单价贵了10元.(1)、求该商家第一次购进冰墩墩多少个?(2)、若所有冰墩墩都按相同的标价销售,要求全部销售完后的利润率不低于20%(不考虑其他因素),那么每个冰墩墩的标价至少为多少元?24. 如图,在 中, ,点O在 上, ,点D在 上,以点O为圆心, 为半径作圆,交 的延长线于点E , 交 于点F , .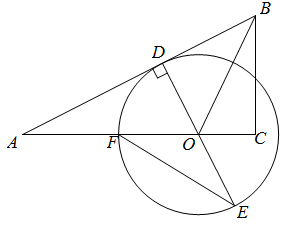 (1)、求证: 为⊙O的切线;(2)、若⊙O的半径为3, ,求 的长.25.(1)、【问题情境】
(1)、求证: 为⊙O的切线;(2)、若⊙O的半径为3, ,求 的长.25.(1)、【问题情境】
如图1,在正方形ABCD中,E,F,G分别是BC,AB,CD上的点,FG⊥AE于点Q.求证:AE=FG.
(2)、【尝试应用】如图2,正方形网格中,点A,B,C,D为格点,AB交CD于点O.求tan∠AOC的值;
(3)、【拓展提升】如图3,点P是线段AB上的动点,分别以AP,BP为边在AB的同侧作正方形APCD与正方形PBEF,连接DE分别交线段BC,PC于点M,N.
①求∠DMC的度数;
②连接AC交DE于点H,直接写出的值.
26. 如图,已知二次函数的图象与轴交于、两点,与轴交于点 , 其对称轴与轴交于点 , 连接、 . 点为抛物线上的一个动点(与点、、不重合),设点的横坐标为 , 的面积为 . (1)、求此二次函数的表达式;(2)、当点在第一象限内时,求关于的函数表达式;(3)、若点在轴上方,的面积能否等于的面积?若能,求出此时点的坐标,若不能,请说明理由.
(1)、求此二次函数的表达式;(2)、当点在第一象限内时,求关于的函数表达式;(3)、若点在轴上方,的面积能否等于的面积?若能,求出此时点的坐标,若不能,请说明理由.