辽宁省大连市八区2022年民间协作联盟中考模拟考试数学试卷

试卷更新日期：2022-07-13 类型：中考模拟

进入出卷网下载

一、单选题

1. -2021的相反数是（）

A、-2021 B、2021 C、 $- \frac{1}{2020}$ D、 $\frac{1}{2020}$

查看试题解析
2. 根据统计数据，2019年春晚直播期间，通过电视、网络及其他终端收看节目的观众达11.73亿人，将11.73亿用科学记数法表示正确的是（）

A、11.73× $1 0^{8}$ B、11.73× $1 0^{9}$ C、1.173× $1 0^{8}$ D、1.173× $1 0^{9}$

查看试题解析
3. 有一个正方体原料，挖去一个小正方体，得到如图所示的零件，则这个零件的主视图是（）

A、 B、 C、 D、

查看试题解析
4. 下列由左到右的变形，属于因式分解的是（）

A、（x+2）（x﹣2）＝ $x^{2}$ ﹣4 B、 $x^{2}$ +4x+4＝x（x+4）+4 C、a $x^{2}$ ﹣4a＝a（ $x^{2}$ ﹣4） D、 $x^{2}$ +3﹣4x＝（x﹣1）（x﹣3）

查看试题解析
5. 某市一楼盘准备以每平方米8000元的均价对外销售，由于国务院有关房地产的新政策出台后，购房者持币观望，为了加快资金周转，房地产开发商对价格经过连续两次下调后，决定以每平方米7220元的均价开盘销售，则平均每次下调的百分率是（）

A、4.875% B、5% C、5.4% D、10%

查看试题解析
6. 已知 $a$ ， $b$ 是方程 $x^{2} + x - 3 = 0$ 的两个实数根，则 $a^{2} - b + 2019$ 的值是（）

A、2023 B、2021 C、2020 D、2019

查看试题解析
7. 甲、乙两班学生举行1分钟跳绳比赛，参赛学生每分钟跳绳个数的统计结果如下表：
班级
参加人数
平均数
中位数
方差
甲班
55
175
189
291
乙班
55
175
191
210
某同学分析上表后得出如下结论：①甲、乙两班学生的平均成绩相同；②乙班优秀的人数多于甲班优秀的人数（每分钟跳绳的个数≥190为优秀）；③甲班成绩的波动比乙班大．上述结论中，正确的是（）

A、①② B、②③ C、①③ D、①②③

查看试题解析
8. 下列计算中，错误的是（）

A、 $5 a^{3} - a^{3} = 4 a^{3}$ B、 $(- a)^{2} \cdot a^{3} = a^{5}$ C、 $(a - b)^{3} \cdot (b - a)^{2} = (a - b)^{5}$ D、 $2^{m} \cdot 3^{n} = 6^{m + n}$

查看试题解析
9. 如图，在矩形纸片ABCD中，AB=3，点E在边BC上，将△ABE沿直线AE折叠，点B恰好落在对角线AC上的点F处，若∠EAC=∠ECA，则AC的长是（）

A、 $3 \sqrt{3}$ B、6 C、4 D、5

查看试题解析
10. 二次函数 $y = a x^{2} + b x + c$ 的部分对应值如下表：
x
…
-3
-2
0
1
3
5
…
y
…
7
0
-8
-9
-5
7
…
二次函数 $y = a x^{2} + b x + c$ 图象的对称轴为 $x = a ， x = 2$ 对应的函数值 $y = b$ ．则a、b的值为（）

A、 $a = 1 ， b = 0$ B、 $a = 0 ， b = - 8$ C、 $a = 1 ， b = - 8$ D、 $a = 1 ， b = - 5$

查看试题解析

二、填空题

11. $- \frac{64}{27}$ 的立方根是

查看试题解析
12. 如图，在一笔直的海岸线l上有A、B两个观测站， $A B = 2 k m$ ，从A测得船C在北偏东 $45 °$ 的方向，从B测得船C在北偏东 $22.5 °$ 的方向．则 $∠ A C B$ 的度数．

查看试题解析
13. 已知一块圆心角为300°的扇形铁皮，用它做一个圆锥形的烟囱帽（接缝忽略不计），若圆锥的底面圆的直径是80cm，则这块扇形铁皮的半径是cm.

查看试题解析
14. 《九章算术》是中国古代第一部数学专著，也是世界上最早的印刷本数学书它的出现标志着中国古代数学体系的形成．《九章算术》早在隋唐时期即已传入朝鲜、日本并被译成日、俄、德、法等多种文字版本，书中有如下问题：今有共买物，人出八，盈三；人出七，不足四．问人数、物价各几何？设有x人，该物品价值y元，可得出关于x，y的二元一次方程组为．

查看试题解析
15. 若反比例函数y＝﹣ $\frac{2}{x}$ 的图象上有两个不同的点，它们关于y轴的对称点都在一次函数y＝﹣x+m的图象上，则m的取值范围是．

查看试题解析
16. 如图，矩形 $A B C D$ 中， $A B = 6 ， A D = 8$ ，点E在边 $A D$ 上， $C E$ 与 $B D$ 相交于点F．设 $D E = x$ ， $B F = y$ ，当 $0 ⩽ x ⩽ 8$ 时，y关于x的函数解析式为．

查看试题解析

三、解答题

17. 计算：（﹣1）²⁰¹⁹﹣（2﹣ $\sqrt{5}$ ）⁰+cos²45°．

查看试题解析
18. 解方程： $x^{2} + 4 x - 8 = 0$ ．

查看试题解析
19. 如图，BE是△ABC的角平分线，延长BE至D，使得BC=CD．

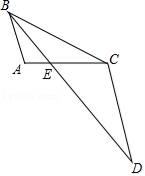(1)、求证：△AEB∽△CED；

(2)、若AB=2，BC=4，AE=1，求CE长．

查看试题解析
20. 某校根据《教育部基础教育课程教材发展中心中小学生阅读指导目录（2020版）》公布的初中段阅读书目，开展了读书活动，六月末，学校对八年级学生在此次活动中的读书量进行了抽样调查，如图是根据调查结果绘制的统计图表的一部分
读书量
频数（人）
频率
1本
4
2本
0.3
3本
4本及以上
10
根据以上信息，解答下列问题：

(1)、被调查学生中，读书量为1本的学生数为4人，读书量达到4本及以上的学生数占被调查学生总人数的百分比为%；

(2)、被调查学生的总人数为人，其中读书量为2本的学生数为人；

(3)、若该校八年级共有550名学生，根据调查结果，估计该校八年级学生读书量为3本的学生人数．

查看试题解析
21. 如图，从热气球C上测得两建筑物A、B底部的俯角分别为29.5°和45°，如果这时气球的高度CD为80米，且点A、D、B在同一直线上，求建筑物A、B之间的距离（结果精确到1米）．[参考数据：sin29.5°＝0.49，cos29.5°＝0.87，tan29.5°＝0.57]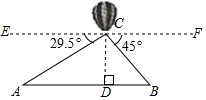

查看试题解析
22. 如图，以Rt△ABC的直角边AB为直径作⊙O，交斜边AC于点D，点E为OB的中点，连接CE并延长交⊙O于点F，点F恰好落在 $\overset{⌢}{A B}$ 的中点，连接AF并延长与CB的延长线相交于点G，连接OF.

(1)、求证：OF＝ $\frac{1}{2}$ BG；

(2)、若AB＝4，求DC的长．

查看试题解析
23. 甲、乙两个探测气球分别从海拔 $5 m$ 和 $15 m$ 处同时出发，匀速上升 $60 min$ .下图是甲、乙两个探测气球所在位置的海拔y（单位：m）与气球上升时间x（单位： $\min$ ）的函数图象.

(1)、求这两个气球在上升过程中y关于x的函数解析式；

(2)、当这两个气球的海拔高度相差 $15 m$ 时，求上升的时间.

查看试题解析
24. 将一个直角三角形纸片 $A B O$ ，放置在平面直角坐标系中，边 $A B$ 所在直线 $y = - \frac{\sqrt{3}}{3} x + 1$ 与x轴、y轴分别相交于点A，B点M在射线 $A O$ 上（点M不与点P、A重合）过点M作 $M N ⊥ A B$ 于点N，沿着 $M N$ 折叠该纸片，顶点A的对应点为 $A^{'}$ ，设点M的坐标为 $(m ， 0)$ ，折叠后的 $Δ A^{'} M N$ 与 $Δ A O B$ 重叠部分的面积为S．

(1)、填空：直接写出点A，B的坐标A ， B ， $∠ B A O =$ °；

(2)、当点 $A^{'}$ 与顶点B重合时，直接写出点M的坐标．

(3)、求S关于m的函数关系式，并写出自变量m的取值范围．

查看试题解析
25. 已知，如图 $Δ A B C$ 中， $B D$ 是中线，点E是 $A B$ 上一点， $C E$ 与 $B D$ 交于点F， $E B = E F$ ．

(1)、在图中与 $∠ D F C$ 相等的角有和；

(2)、在图中找出与线段 $A B$ 相等的线段并证明；

(3)、若 $A B = k A C$ ，且 $∠ A D B = 90 ° - \frac{1}{2} ∠ A B D$ ，求 $\frac{B F}{D F}$ 的值．（用含k的代数式表示）

查看试题解析
26. 已知抛物线G： $y = (m + 1) x^{2} + 2 (n - 1) x + n + 1$ （ $m \neq - 1$ ， m为常数）的对称轴与直线 $y = k x + k$ （ $k > 0$ ， k为常数）相交于x轴上一点P．

(1)、求m与n的数量关系；

(2)、若直线 $y = k x + k$ 与y轴交于点Q，且 $O Q = O P$ ，
①把直线 $y = k x + k$ 绕点Q顺时针旋转 $45 °$ 得到的直线与抛物线G相交于A、B两点，若 $A B = 4$ ，求m的值；
②将直线 $y = k x + k$ 向上平移 $2 k$ 个单位，得到的直线与抛物线G的两个交点的横坐标 $x_{1} ， x_{2}$ 满足 $- 2 < x_{1} < x_{2} < 2$ ，求m的取值范围．

查看试题解析

班级	参加人数	平均数	中位数	方差
甲班	55	175	189	291
乙班	55	175	191	210

读书量	频数（人）	频率
1本	4
2本		0.3
3本
4本及以上	10

x	…	-3	-2	0	1	3	5	…
y	…	7	0	-8	-9	-5	7	…