江西省九江市2022年初中学业水平模拟试卷数学二模
试卷更新日期:2022-07-13 类型:中考模拟
一、单选题
-
1. 实数2022的相反数是( )A、2022 B、-2022 C、 D、2. 下列各式中计算正确的是( )A、x+x3=x4 B、(x﹣4)2=x8 C、x﹣2•x5=x3 D、x8÷x2=x4(x≠0)3. 如图所示几何体的左视图是( )
 A、
A、 B、
B、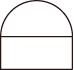 C、
C、 D、
D、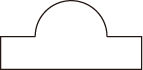 4. 甲、乙两人一周中每天制作工艺品的数量如图所示,则对甲、乙两人每天制作工艺品数量描述正确的是( )
4. 甲、乙两人一周中每天制作工艺品的数量如图所示,则对甲、乙两人每天制作工艺品数量描述正确的是( ) A、甲比乙稳定 B、乙比甲稳定 C、甲与乙一样稳定 D、无法确定5. 在同一坐标系中,函数 和 的图像大致是( )A、
A、甲比乙稳定 B、乙比甲稳定 C、甲与乙一样稳定 D、无法确定5. 在同一坐标系中,函数 和 的图像大致是( )A、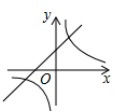 B、
B、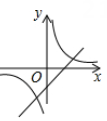 C、
C、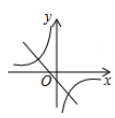 D、
D、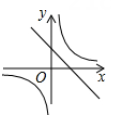 6. 如图,在一单位为1的方格纸上,△A1A2A3 , △A3A4A5 , △A5A6A7…,都是斜边在x轴上,斜边长分别为2,4,6,…的等腰直角三角形,若A1A2A3的顶点坐标分别为A1(2,0),A2(1,−1),A3(0,0),则依图中所示规律,A2022的坐标为( )
6. 如图,在一单位为1的方格纸上,△A1A2A3 , △A3A4A5 , △A5A6A7…,都是斜边在x轴上,斜边长分别为2,4,6,…的等腰直角三角形,若A1A2A3的顶点坐标分别为A1(2,0),A2(1,−1),A3(0,0),则依图中所示规律,A2022的坐标为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
7. 因式分解: .
8. 截至2021年10月30日,电影《长津湖》的累计票房达到大约5500000000元,数据5500000000用科学记数法表示为 .9. 设m、n分别为一元二次方程的两个实数根,则m+n+mn的值为 .10. 某品牌汽车为了打造更加精美的外观,特将汽车倒车镜设计为整个车身黄金分割点的位置(如图,即车尾到倒车镜的距离与车长之比为0.618),若车头与倒车镜的水平距离为 , 则该车车身总长约为(保留整数).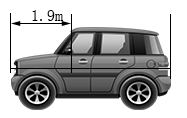 11. 如图,在四边形中, , , 分别是 , , 的中点, , , 则的度数为 .
11. 如图,在四边形中, , , 分别是 , , 的中点, , , 则的度数为 . 12. 如图,直线y=−x+与坐标轴分别交于A,B两点,在平面直角坐标系内有一点C,使△ABC与△ABO全等,则点C的坐标为 .
12. 如图,直线y=−x+与坐标轴分别交于A,B两点,在平面直角坐标系内有一点C,使△ABC与△ABO全等,则点C的坐标为 .
三、解答题
-
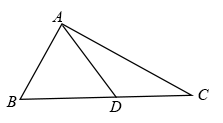
13.(1)、;(2)、如图,已知在△ABC中,D是BC上的一点,∠BAC=90°,∠DAC=∠C.求证:AD=BD.
 14. 解不等式组 ,并把解集在数轴上表示出来15. 北京冬奥会的胜利召开,也有很多志愿者的一份功劳.北京师范大学数学系的小丽、小王和三个同学共五个志愿者被派往国家体育馆,根据该场馆人事安排而要先抽出一人去做安保服务,再派两人去做交通服务,请你利用所学知识完成下列问题.(1)、小丽被派去做安保服务的概率是;(2)、若定了一位同学去做安保服务,请你利用画树状图或列表的方法,求出小丽和小王同时被派去做交通服务的概率.16. 如图,为正五边形的外接圆,已知 , 请用无刻度直尺完成下列作图,保留必要的画图痕迹.
14. 解不等式组 ,并把解集在数轴上表示出来15. 北京冬奥会的胜利召开,也有很多志愿者的一份功劳.北京师范大学数学系的小丽、小王和三个同学共五个志愿者被派往国家体育馆,根据该场馆人事安排而要先抽出一人去做安保服务,再派两人去做交通服务,请你利用所学知识完成下列问题.(1)、小丽被派去做安保服务的概率是;(2)、若定了一位同学去做安保服务,请你利用画树状图或列表的方法,求出小丽和小王同时被派去做交通服务的概率.16. 如图,为正五边形的外接圆,已知 , 请用无刻度直尺完成下列作图,保留必要的画图痕迹.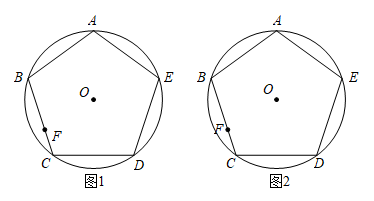 (1)、在图1中的边上求作点 , 使;(2)、在图2中的边上求作点 , 使 .17. 如图,一次函数y=kx+b的图象与反比例函数y=−的图象相交于A(−1,m)和B(n,−1)两点.
(1)、在图1中的边上求作点 , 使;(2)、在图2中的边上求作点 , 使 .17. 如图,一次函数y=kx+b的图象与反比例函数y=−的图象相交于A(−1,m)和B(n,−1)两点. (1)、 m= , n=;(2)、求出一次函数的解析式,并结合图象直接写出不等式kx+b>−的解集.18. 2022年北京冬季奥运会吉样物冰墩墩大受欢迎.某商店第一次用4000元购进某款冰墩墩纪念章,很快卖完.第二次又用3000购进该款纪念章,但这次每个纪念章是第一次进价的1.2倍,数量比第一次少了30个.(1)、求第一次每个纪念章的进价是多少元?(2)、若第二次进货后按80元/个的价格出售,恰好销售完一半时,根据市场情况,商店决定对剩余的纪念章按同一标准一次性打折销售,但要求这次的利润不少于600元,问最低可打几折?19. 某校八年级学生全部参加“初二生物地理会考”,从中抽取了部分学生的生物考试成绩,将他们的成绩进行统计后分为 , , , 四等,并将统计结果绘制成如下的统计图,请结合图中所给的信息解答下列问题(说明:测试总人数的前30%考生为等级,前30%至前70%为等级,前70%至前90%为等级,90%以后为等级)
(1)、 m= , n=;(2)、求出一次函数的解析式,并结合图象直接写出不等式kx+b>−的解集.18. 2022年北京冬季奥运会吉样物冰墩墩大受欢迎.某商店第一次用4000元购进某款冰墩墩纪念章,很快卖完.第二次又用3000购进该款纪念章,但这次每个纪念章是第一次进价的1.2倍,数量比第一次少了30个.(1)、求第一次每个纪念章的进价是多少元?(2)、若第二次进货后按80元/个的价格出售,恰好销售完一半时,根据市场情况,商店决定对剩余的纪念章按同一标准一次性打折销售,但要求这次的利润不少于600元,问最低可打几折?19. 某校八年级学生全部参加“初二生物地理会考”,从中抽取了部分学生的生物考试成绩,将他们的成绩进行统计后分为 , , , 四等,并将统计结果绘制成如下的统计图,请结合图中所给的信息解答下列问题(说明:测试总人数的前30%考生为等级,前30%至前70%为等级,前70%至前90%为等级,90%以后为等级)
 (1)、求抽取了多少名学生成绩;(2)、学生成绩的中位数落在组;(3)、请把频数分布直方图补充完整;(4)、若测试总人数前90%为合格,该校初二年级有900名学生,求全年级生物合格的学生共约多少人.20. 如图1是一个长方体形家用冰箱,长、宽、高分别为0.5米、0.5米、1.7米,在搬运上楼的过程中,由于楼梯狭窄,只能靠一名搬运师傅背上楼.
(1)、求抽取了多少名学生成绩;(2)、学生成绩的中位数落在组;(3)、请把频数分布直方图补充完整;(4)、若测试总人数前90%为合格,该校初二年级有900名学生,求全年级生物合格的学生共约多少人.20. 如图1是一个长方体形家用冰箱,长、宽、高分别为0.5米、0.5米、1.7米,在搬运上楼的过程中,由于楼梯狭窄,只能靠一名搬运师傅背上楼.

 (1)、如图2,为便于搬运师傅起身,冰箱通常与地面成角,求此时点与地面的高度;(2)、如图3,在搬运过程中,冰箱与水平面成夹角,最低点与地面高度为0.3米,门的高度为2米,假如最高点与门高相同时,刚好可以搬进去,若他保持冰箱与平面夹角不变,他要下蹲几厘米才刚好进门?(结果精确到厘米, , , )21. 如图,以△ABC的一边AB为直径的半圆O与边AC,BC的交点分别为点 E,点 D,且D是 的中点.
(1)、如图2,为便于搬运师傅起身,冰箱通常与地面成角,求此时点与地面的高度;(2)、如图3,在搬运过程中,冰箱与水平面成夹角,最低点与地面高度为0.3米,门的高度为2米,假如最高点与门高相同时,刚好可以搬进去,若他保持冰箱与平面夹角不变,他要下蹲几厘米才刚好进门?(结果精确到厘米, , , )21. 如图,以△ABC的一边AB为直径的半圆O与边AC,BC的交点分别为点 E,点 D,且D是 的中点.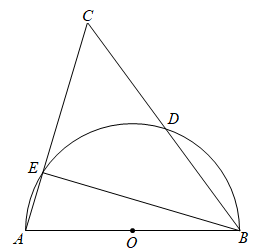 (1)、若∠A=80°,求∠DBE的度数.(2)、求证:AB=AC.(3)、若⊙O 的半径为5cm,BC=12cm,求线段BE的长.22. 如图,抛物线与轴交于点 , 与轴交于点 , 点为线段上一动点,过点且垂直于轴的直线与直线及抛物线分别交于点 , .
(1)、若∠A=80°,求∠DBE的度数.(2)、求证:AB=AC.(3)、若⊙O 的半径为5cm,BC=12cm,求线段BE的长.22. 如图,抛物线与轴交于点 , 与轴交于点 , 点为线段上一动点,过点且垂直于轴的直线与直线及抛物线分别交于点 , . (1)、求抛物线的解析式,并写出此抛物线的对称轴;(2)、如果以点、、、为顶点的四边形为平行四边形,求的值;(3)、若与面积相等,直接写出点的坐标.23. 如图
(1)、求抛物线的解析式,并写出此抛物线的对称轴;(2)、如果以点、、、为顶点的四边形为平行四边形,求的值;(3)、若与面积相等,直接写出点的坐标.23. 如图

 (1)、问题发现:如图1,点为平面内一动点,且 , , 则的最小值为 , 的最大值为;(2)、轻松尝试:如图2,在矩形中, , , 为边的中点,是边上的动点,将沿所在直线折叠得到 , 连接 , 则的最小值为;(3)、方法运用:在四边形中, , , , .
(1)、问题发现:如图1,点为平面内一动点,且 , , 则的最小值为 , 的最大值为;(2)、轻松尝试:如图2,在矩形中, , , 为边的中点,是边上的动点,将沿所在直线折叠得到 , 连接 , 则的最小值为;(3)、方法运用:在四边形中, , , , .①如图3,当时,求线段的最大值;
②如图4,当时,用含的式子表示线段的最大值.