江西省吉安市遂川县2022年九年级初中学业水平第一次模拟考数学试题
试卷更新日期:2022-07-13 类型:中考模拟
一、单选题
-
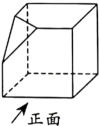
1. 的倒数是( )A、 B、 C、3 D、-32. 2021年度我国新能源汽车全年累计突破298.9万台,有关部门估计2022年我国新能源汽车销量将增长到500万台,将500万用科学记数法表示应为( )A、 B、 C、 D、3. 如图所示,将一个正方体切去一个角,则所得几何体的左视图为( )
 A、
A、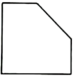 B、
B、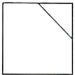 C、
C、 D、
D、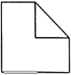 4. 下列运算正确的是()A、 B、 C、 D、5. 关于抛物线 , 下列说法错误的是( ).A、开口向上 B、当时,经过坐标原点O C、不论为何值,都过定点(1,﹣2) D、>0时,对称轴在轴的左侧6. 如图,在矩形中, , , 为矩形内一点, , 连接 , 则的最小值为( )
4. 下列运算正确的是()A、 B、 C、 D、5. 关于抛物线 , 下列说法错误的是( ).A、开口向上 B、当时,经过坐标原点O C、不论为何值,都过定点(1,﹣2) D、>0时,对称轴在轴的左侧6. 如图,在矩形中, , , 为矩形内一点, , 连接 , 则的最小值为( )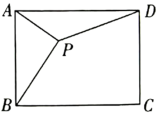 A、8 B、 C、10 D、
A、8 B、 C、10 D、二、填空题
-
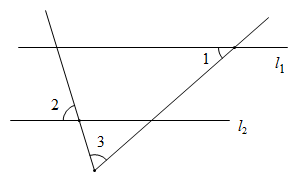
7. 函数y=中自变量x的取值范围是.8. 如图,直线l1∥l2, ∠1=40°,∠2=75°,则∠3等于 .
 9. 不等式组的解集是 .10. 数据: , 3,4,7,1,的平均数是4,则这组数据的众数是 .11. 已知m,n是关于x的一元二次方程的两个根,若 , 则的值为 .12. 如图,正六边形的边长为6, , 分别为 , 的中点,点在正六边形的边上,且在直线的右侧,则当为等腰三角形时,长为 .
9. 不等式组的解集是 .10. 数据: , 3,4,7,1,的平均数是4,则这组数据的众数是 .11. 已知m,n是关于x的一元二次方程的两个根,若 , 则的值为 .12. 如图,正六边形的边长为6, , 分别为 , 的中点,点在正六边形的边上,且在直线的右侧,则当为等腰三角形时,长为 .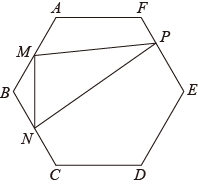
三、解答题
-
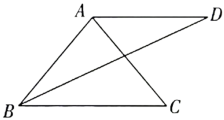
13.(1)、计算:;(2)、如图,已知 , 且 . 求证: .
 14. 先化简,再求值: , 其中 .15. 《九章算术》记载了一个方程的问题,译为:今有上禾6束,减损其中之“实”十八升,与下禾10束之“实”相当;下禾15束,减损其中之“实”五升,与上禾5束之“实”相当.问上、下禾每束之实各为多少升?16. 王某与李某二人在网站上购买高铁票时系统随机分配座位,若系统已将两人分配到一排后,在同一排分配各个座位的概率一样,若一排中座位编号为A, , , , .
14. 先化简,再求值: , 其中 .15. 《九章算术》记载了一个方程的问题,译为:今有上禾6束,减损其中之“实”十八升,与下禾10束之“实”相当;下禾15束,减损其中之“实”五升,与上禾5束之“实”相当.问上、下禾每束之实各为多少升?16. 王某与李某二人在网站上购买高铁票时系统随机分配座位,若系统已将两人分配到一排后,在同一排分配各个座位的概率一样,若一排中座位编号为A, , , , . (1)、“分给二人A,座位”是事件,若分给王某A座后,再给李某座的概率是;(2)、求分给二人相邻座位(过道两侧座位 , 不算相邻)的概率.17. 如图,在⊙中,为弦,为⊙的切线,为切点,请仅用无刻度的直尺按下列要求作图.
(1)、“分给二人A,座位”是事件,若分给王某A座后,再给李某座的概率是;(2)、求分给二人相邻座位(过道两侧座位 , 不算相邻)的概率.17. 如图,在⊙中,为弦,为⊙的切线,为切点,请仅用无刻度的直尺按下列要求作图.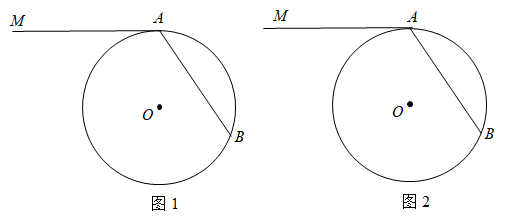 (1)、在图1中,以为边作一个矩形;(2)、在图2中,分别在上取一点 , 在⊙取两点 , , 作 .18. 某教育机构为了了解“双减”政策下学生如何利用空余时间的情况,针对孩子在空余时间的主要四类方式: . 自己安排学习; . 家长检查学校学习情况; . 培养非学科类兴趣爱好; . 看电视或玩手机,在本校学生中随机抽取部分学生进行调查,并进行统计分析,绘制了以下不完整的统计图,请根据图中提供的信息,解答下列问题:
(1)、在图1中,以为边作一个矩形;(2)、在图2中,分别在上取一点 , 在⊙取两点 , , 作 .18. 某教育机构为了了解“双减”政策下学生如何利用空余时间的情况,针对孩子在空余时间的主要四类方式: . 自己安排学习; . 家长检查学校学习情况; . 培养非学科类兴趣爱好; . 看电视或玩手机,在本校学生中随机抽取部分学生进行调查,并进行统计分析,绘制了以下不完整的统计图,请根据图中提供的信息,解答下列问题: (1)、在这次抽样调查中,共调查了名学生;(2)、补全条形统计图,并在扇形统计图中计算类所对应扇形的圆心角的度数;(3)、根据抽样调查结果,估计该校3000名学生中空余时间“看电视或玩手机”的人数.19. 如图,为⊙外一点, , 为⊙上两点, , 垂足为 , 交⊙于点 , 交于 , .
(1)、在这次抽样调查中,共调查了名学生;(2)、补全条形统计图,并在扇形统计图中计算类所对应扇形的圆心角的度数;(3)、根据抽样调查结果,估计该校3000名学生中空余时间“看电视或玩手机”的人数.19. 如图,为⊙外一点, , 为⊙上两点, , 垂足为 , 交⊙于点 , 交于 , .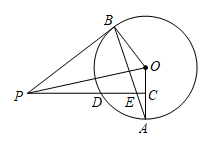 (1)、求证:为⊙的切线;(2)、若 , , 求的长.20. 如图,直线分别与轴、轴交于点 , , 点 , 与反比例函数交于点 , , 点在直线上,且 , 为的中点.
(1)、求证:为⊙的切线;(2)、若 , , 求的长.20. 如图,直线分别与轴、轴交于点 , , 点 , 与反比例函数交于点 , , 点在直线上,且 , 为的中点.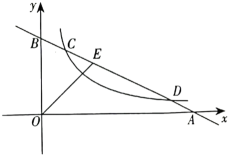 (1)、求反比例函数的解析式;(2)、连接 , 求的值.21. 如图1是某小区门口的门禁自动识别系统,主要由可旋转高清摄像机和其下方固定的显示屏.图2是其结构示意图,摄像机长 , 点为摄像机旋转轴心,为的中点,显示屏的上沿与平行, , 与连接杆 , , , 点到地面的距离为 . 若与水平地面所成的角的度数为 .
(1)、求反比例函数的解析式;(2)、连接 , 求的值.21. 如图1是某小区门口的门禁自动识别系统,主要由可旋转高清摄像机和其下方固定的显示屏.图2是其结构示意图,摄像机长 , 点为摄像机旋转轴心,为的中点,显示屏的上沿与平行, , 与连接杆 , , , 点到地面的距离为 . 若与水平地面所成的角的度数为 .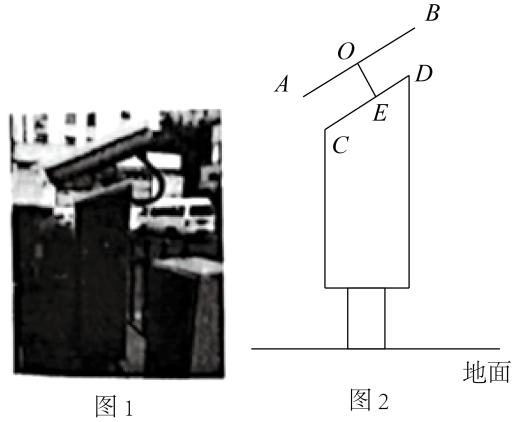 (1)、求显示屏所在部分的宽度;(2)、求镜头到地面的距离.(参考数据: , , , 结果保留一位小数)22. 如图,直线与轴交于点 , 与轴交于点 , 点在线段上,且 . 以点为顶点的抛物线记为;以为顶点的抛物线记为 , 与轴交于点 , .
(1)、求显示屏所在部分的宽度;(2)、求镜头到地面的距离.(参考数据: , , , 结果保留一位小数)22. 如图,直线与轴交于点 , 与轴交于点 , 点在线段上,且 . 以点为顶点的抛物线记为;以为顶点的抛物线记为 , 与轴交于点 , .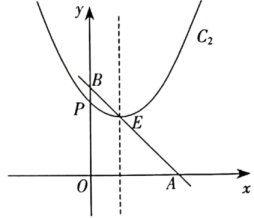 (1)、求抛物线和的表达式,并判断抛物线会经过点;(2)、若抛物线和中的都随的增大而减小,请直接写出此时的取值范围;(3)、在(2)的的取值范围内,设新的函数 , 求出函数与的函数关系式;问当为何值时,函数有最大值,求出这个最大值,并直接写出的取值范围.23. 如图,在正方形中,为边上一点,以为边向右侧作正方形 , 连接交于点 , 的延长线交于点 , 与交于点 .
(1)、求抛物线和的表达式,并判断抛物线会经过点;(2)、若抛物线和中的都随的增大而减小,请直接写出此时的取值范围;(3)、在(2)的的取值范围内,设新的函数 , 求出函数与的函数关系式;问当为何值时,函数有最大值,求出这个最大值,并直接写出的取值范围.23. 如图,在正方形中,为边上一点,以为边向右侧作正方形 , 连接交于点 , 的延长线交于点 , 与交于点 .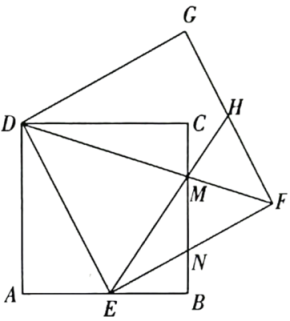 (1)、求证:平分;(2)、若 , 求的值;(3)、点在上运动过程中,是否存在的情况?请说明理由.
(1)、求证:平分;(2)、若 , 求的值;(3)、点在上运动过程中,是否存在的情况?请说明理由.