江苏省泰州市海陵区2022年中考数学一模试题

试卷更新日期：2022-07-13 类型：中考模拟

进入出卷网下载

一、单选题

1. （﹣2）²的值等于（）

A、﹣4 B、4 C、﹣2 D、2

查看试题解析
2. 一块积木如图所示，则它的左视图是（）

A、 B、 C、 D、

查看试题解析
3. 下列计算正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $2 \sqrt{2} + 3 \sqrt{2} = 5 \sqrt{2}$ C、 $\sqrt{2} \times \sqrt{3} = \sqrt{5}$ D、 $2 \sqrt{2} \times 3 \sqrt{2} = 6 \sqrt{2}$

查看试题解析
4. 在▱ABCD中，对角线AC、BD的长分别为4、6，则边BC的长可能为（）

A、4 B、5 C、6 D、7

查看试题解析
5. 小丽同学住在学校附近，某周星期一至星期五早晨步行到校所花时间（单位：分钟）分别为11，10，11，9，x，已知这组数据的平均数为10，则其方差为（）

A、 $\frac{1}{5}$ B、 $\frac{2}{5}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
6. 已知3x﹣y＝3a²﹣6a+9，x+y＝a²+6a﹣10，当实数a变化时，x与y的大小关系是（）

A、x＞y B、x＝y C、x＜y D、x＞y、x＝y、x＜y都有可能

查看试题解析

二、填空题

7. 计算：（﹣3）⁰等于．

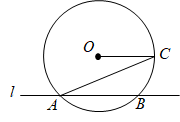
查看试题解析
8. 若二次根式 $\sqrt{x - 2}$ 有意义，则x的取值范围是．

查看试题解析
9. 2022年4月2日，海陵区对封控区、管控区、防范区内全部人员进行了第三轮核酸检测，共采样约343000人，检测结果均为阴性．将数据343000用科学记数法表示为．

查看试题解析
10. 已知某斜面的坡度为1： $\sqrt{3}$ ，那么这个斜面的坡角等于度．

查看试题解析
11. 一次函数y＝kx+3的图象不经过第四象限，则k的取值范围是．

查看试题解析
12. .一个口袋中装有2个红球、1个白球，现小明和小丽用两种不同的方法从袋中随机摸球．小明从袋中一次性随机摸取2个球，都是红球的概率记为P₁；小丽先从袋中随机摸出1个球，记下颜色后放回，再从袋中随机摸出1个球，两次都是红球的概率记为P₂.则P₁与P₂的大小关系是P₁P₂（填“＞”、“＜”或“＝”）．

查看试题解析
13. 用半径为30，圆心角为120°的扇形纸片围成一个圆锥的侧面，则这个圆锥的底面圆半径为.

查看试题解析
14. 当x取任意实数时，二次函数 y=x²－(2m+1)x+m²的值始终为正数，则m的取值范围是.

查看试题解析
15. 如图，直线l与圆O相交于A、B两点，AC是圆O的弦，OC∥AB，半径OC的长为10，弦AB的长为12，动点P从点A出发以每秒1个单位的速度沿射线AB方向运动．当△APC是直角三角形时，动点P运动的时间t为秒．

查看试题解析
16. 如图，点E在正方形ABCD的边BC上，连接DE、BD，延长CB到点F，使BF＝CE，过点E作EG⊥BD于点G，连接FG．若DE＝ $4 \sqrt{3}$ ，则FG的长为．

查看试题解析

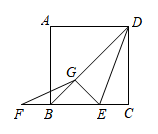
三、解答题

17.

(1)、分解因式：3a²﹣6a+3；

(2)、解方程：x²﹣4x+2＝0．

查看试题解析
18. 为进一步提高学生的英语口语听力水平，某校准备开展英语口语听力比赛．九（1）班准备从甲、乙两人中推荐1人参加比赛，现将两人在班级选拔赛中，5次的测试成绩（总分100分）绘制成如图所示的折线统计图（图中只标注了部分数据）．观察统计图，回答下列问题：

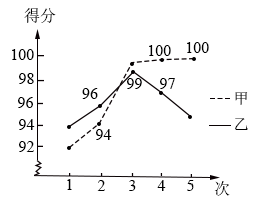(1)、甲5次测试成绩的众数为分；乙5次测试成绩的中位数为分；

(2)、小红认为：应该选择两人中5次测试成绩方差小的去比赛．你同意他的观点吗？请结合统计图说明理由．

查看试题解析
19. 小明在学习完电学知识后，用四个开关A、B、C、D，一个电源和一个灯泡设计了一个如图所示的电路图．

(1)、在开关A闭合的情况下，任意闭合B、C、D中的一个开关，则灯泡发光的概率等于；

(2)、任意闭合其中两个开关，请用树状图或列表的方法求出灯泡发光的概率．

查看试题解析
20. 如图，在△ABC中，∠BAC＝90°，AB＝AC．请用无刻度的直尺和圆规作出符合下列条件的图形，不写作法，保留作图痕迹．

(1)、在线段BC的延长线上，找出一点E，使∠CEA＝22.5°；

(2)、在（1）的条件下，在线段BC上，找出一点D，使∠EAD＝45°．

查看试题解析
21. 已知：如图，AB是⊙O的直径，AC是⊙O的弦，过点C的直线交AB延长线于点D，给出下列信息：
①∠A＝30°；
②CD是⊙O的切线；
③OB＝BD．

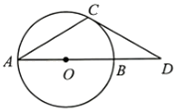(1)、请在上述3条信息中选择其中两条作为条件，剩下的一条作为结论．你选择的条件是 ▲ ，结论是 ▲ （只要填写序号）．判断结论是否正确，并说明理由；

(2)、在（1）的条件下，若CD＝3 $\sqrt{3}$ ，求 $\overset{⌢}{B C}$ 的长度．

查看试题解析
22. 某市为积极响应“绿水青山就是金山银山”的号召，加强了河道整治．某工程队原计划在规定时间内整治河道1500m，实际施工时工作效率提高了20%，结果提前2天完成，求原计划规定多少天完成？

查看试题解析
23. 如图1是一种手机支架，图2是其侧面结构示意图．托板 $A B$ 固定在支撑板顶端的点 $C$ 处，托板 $A B$ 可绕点 $C$ 转动，支撑板 $C D$ 可绕点 $D$ 转动．现量得 $C D = 10 c m$ ， $A C = 12 c m$ ．

(1)、当支撑板 $C D$ 与底座 $D E$ 的夹角 $(∠ C D E)$ 为 $60 °$ 时，求点 $C$ 到底座 $D E$ 的距离；（结果保留根号）

(2)、小强在使用过程中发现，当 $∠ C D E$ 为 $60 °$ 且 $∠ A C D$ 为 $105 °$ 时，此支架使用起来最舒适，求此时点 $A$ 到底座 $D E$ 的距离． (结果精确到 $0.1$ ， $\sqrt{2} \approx 1.41$ ， $\sqrt{3} \approx 1.73$ )

查看试题解析
24. 2022年春，新冠肺炎有所蔓延，市场对口罩的需求量仍然较大．某公司销售一种进价为12元/袋的口罩，其销售量y （万袋）与销售价格x （元/袋）的变化如表：
价格x（元/袋）
…
14
16
18
20
…
销售量y（万袋）
…
5
4
3
2
…
另外，销售过程中的其他开支（不含进价）总计6万元．

(1)、根据表中数据变化规律及学过的“一次函数、二次函数、反比例函数”知识，请判断销售量y （万袋）与价格x （元/袋）满足什么函数？并求出y与x之间的函数表达式；

(2)、设该公司销售这种口罩的净利润为w （万元），当销售价格定为多少元时净利润最大，最大值是多少？

查看试题解析
25. 如图，动点P在函数y $= \frac{3}{x}$ （x＞0）的图象上，过点P分别作x轴和y轴的平行线，交函数y $= - \frac{1}{x}$ 的图象于点A、B，连接AB、OA、OB．设点P横坐标为a．

(1)、直接写出点P、A、B的坐标（用a的代数式表示）；

(2)、点P在运动的过程中，△AOB的面积是否为定值？若是，求出此定值；若不是，请说明理由；

(3)、在平面内有一点Q （ $\frac{1}{3}$ ， 1），且点Q始终在△PAB的内部（不包含边），求a的取值范围．

查看试题解析
26. 如图，在矩形ABCD中，AD＝10，点E是AD上一点，且AE＝m （m是常数），作△BAE关于直线BE的对称图形△BFE，延长EF交直线BC于点G．

(1)、求证：EG＝BG；

(2)、若m＝2．
①当AB＝6时，问点G是否与点C重合，并说明理由；
②当直线BF经过点D时，直接写出AB的长；

(3)、随着AB的变化，是否存在常数m，使等式BG $- \frac{1}{2}$ AE＝AB²总成立？若存在，求出m的值；若不存在，请说明理由．

查看试题解析

价格x（元/袋）	…	14	16	18	20	…
销售量y（万袋）	…	5	4	3	2	…