黑龙江省哈尔滨市香坊区2022年初中毕业学年调研测试(一)数学试卷
试卷更新日期:2022-07-13 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、7 B、﹣7 C、- D、2. 下列运算一定正确的是( )A、 B、 C、 D、3. 下面的几何体中,主(正)视图为三角形的是( )A、
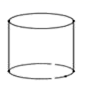 B、
B、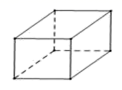 C、
C、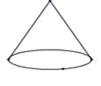 D、
D、 4. 国家体育场“鸟巢”的建筑面积是258 000m2 , 将258 000用科学记数法可表示为( )m2.A、 B、 C、 D、5. 抛物线向右平移1个单位长度,再向下平移3个单位长度后得到的抛物线的解析式为( )A、 B、 C、 D、6. 如果弧长为4cm的扇形面积为16cm2 , 那么该扇形的半径为( )A、8cm B、9cm C、10cm D、11cm7. 已知反比例函数 . 下列结论错误的是( )A、其图象经过点(-7,1) B、其图象在第二、四象限 C、当时,y随x的增大而增大 D、当时,8. 如图,某水库堤坝横断面迎水坡AB的坡比是1: ,堤坝高BC=50m,则应水坡面AB的长度是( )
4. 国家体育场“鸟巢”的建筑面积是258 000m2 , 将258 000用科学记数法可表示为( )m2.A、 B、 C、 D、5. 抛物线向右平移1个单位长度,再向下平移3个单位长度后得到的抛物线的解析式为( )A、 B、 C、 D、6. 如果弧长为4cm的扇形面积为16cm2 , 那么该扇形的半径为( )A、8cm B、9cm C、10cm D、11cm7. 已知反比例函数 . 下列结论错误的是( )A、其图象经过点(-7,1) B、其图象在第二、四象限 C、当时,y随x的增大而增大 D、当时,8. 如图,某水库堤坝横断面迎水坡AB的坡比是1: ,堤坝高BC=50m,则应水坡面AB的长度是( )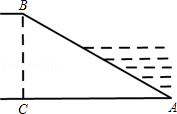 A、100m B、100 m C、150m D、50 m9. 如图, , AF交BE于点G,若AC=CG,AG=FG,则下列结论错误的是( )
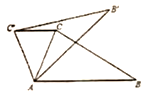
A、100m B、100 m C、150m D、50 m9. 如图, , AF交BE于点G,若AC=CG,AG=FG,则下列结论错误的是( ) A、 B、 C、 D、10. 抛物线与x轴交于点A(-1,0),点B(3,0),交y轴于点C,直线经过点C,点B(3,0),它们的图象如图所示,有以下结论:
A、 B、 C、 D、10. 抛物线与x轴交于点A(-1,0),点B(3,0),交y轴于点C,直线经过点C,点B(3,0),它们的图象如图所示,有以下结论:①抛物线对称轴是直线;②;③时,;④若 , 则 . 其中正确的个数为( )
 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 计算 的结果是.12. 在函数中,自变量x的取值范围为 .13. 把多项式ab2﹣a分解因式的结果是 .14. 不等式组的解集为 .15. 如图,在中, , 在同一平面内,将绕点旋转到的位置,使得 , 则的度数等于.
 16. 不透明的袋子中装有红、蓝小球各一个,除颜色外无其他差别,随机摸出一个小球后,放回并摇匀,再随机摸出一个,两次都摸到相同颜色的小球的概率是.17. 如图,AB、AC是⊙O的弦,点D是CA延长线上的点. , 若 , 则∠BOC的度数是°.
16. 不透明的袋子中装有红、蓝小球各一个,除颜色外无其他差别,随机摸出一个小球后,放回并摇匀,再随机摸出一个,两次都摸到相同颜色的小球的概率是.17. 如图,AB、AC是⊙O的弦,点D是CA延长线上的点. , 若 , 则∠BOC的度数是°. 18. 某年全国足球甲级A组的前11场比赛中,某队保持连续不败,共积23分,按比赛规则,胜一场得3分,平一场得1分,那么该队共胜了场.19. 在Rt△ABC中, , 斜边AC的垂直平分线交射线CB于点E,交射线AB于点F,若 , , 则线段BF的长为 .20. 如图,在 中,点 是 边上的一点,且 ,连接 并取 的中点 ,连接 ,若 ,且 ,则 的长为 .
18. 某年全国足球甲级A组的前11场比赛中,某队保持连续不败,共积23分,按比赛规则,胜一场得3分,平一场得1分,那么该队共胜了场.19. 在Rt△ABC中, , 斜边AC的垂直平分线交射线CB于点E,交射线AB于点F,若 , , 则线段BF的长为 .20. 如图,在 中,点 是 边上的一点,且 ,连接 并取 的中点 ,连接 ,若 ,且 ,则 的长为 .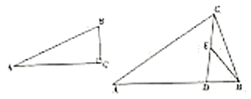
三、解答题
-
21. 先化简,再求代数式的值.其中a=2sin60°﹣3tan45°.22. 如图所示,在的方格纸中,每个小正方形的边长均为1,线段AB、线段CD的端点均在小正方形的顶点上.
 (1)、在图中画出以AB为底边,面积为5的等腰△ABE,且点E在小正方形的顶点上;(2)、在图中画出以CD为斜边的Rt△CDF,∠DCF正切值为 , 且点F在小正方形的顶点上,连接AF,请直接写出线段AF的长.23. 某中学开展课外读书活动,为了解学生的读书情况,小明同学三月份随机抽取部分学生,并对抽取的每名学生的读书次数进行了统计,绘制成图1和图2两幅不完整的统计图,请根据图上信息,回答下列问题:
(1)、在图中画出以AB为底边,面积为5的等腰△ABE,且点E在小正方形的顶点上;(2)、在图中画出以CD为斜边的Rt△CDF,∠DCF正切值为 , 且点F在小正方形的顶点上,连接AF,请直接写出线段AF的长.23. 某中学开展课外读书活动,为了解学生的读书情况,小明同学三月份随机抽取部分学生,并对抽取的每名学生的读书次数进行了统计,绘制成图1和图2两幅不完整的统计图,请根据图上信息,回答下列问题: (1)、本次抽取的学生有多少人?(2)、请你通过计算,将图2的统计图补充完整;(3)、该中学有1500名学生,如果规定该月读书5次以上(含5次)为“读书优秀学员”,估计该中学有多少名学生为“读书优秀学员”人数.24. 已知正方形ABCD,点E在边BC上,连接AE, , 交AE于点G,交CD于点F.
(1)、本次抽取的学生有多少人?(2)、请你通过计算,将图2的统计图补充完整;(3)、该中学有1500名学生,如果规定该月读书5次以上(含5次)为“读书优秀学员”,估计该中学有多少名学生为“读书优秀学员”人数.24. 已知正方形ABCD,点E在边BC上,连接AE, , 交AE于点G,交CD于点F. (1)、如图1,求证:;(2)、如图2,AC、BD交于点O,AE交BD于点M,AC交BF于点N, , 交CD于点P,PQ⊥BD于点Q,连接PN, , 在不添加辅助线的情况下,请你直接写出与线段BM相等的所有线段(除线段BM外).25. 捷报电脑公司生产一批电脑,每台电脑的出厂价比成本价多1000元;若每台电脑的出厂价不变,成本价提高了12.5%,此时每台电脑仍可获利500元.(1)、求该品牌电脑的成本价和出厂价分别是多少元?(2)、频传公司在捷报电脑公司以出厂价购进一批电脑,第一个月以比出厂价提高20%的价格销售30台电脑;第二个月以第一个月销售价九折的价格,将剩余的电脑全部售完,若两个月售出电脑所获得的总利润不低于38000元,求频传公司至少购进了多少台电脑?26. 已知:BC为⊙O的弦,点A为⊙O上一点,连接AB,点K在AB上,连接CK,OK,∠AKC= 2∠ABC.
(1)、如图1,求证:;(2)、如图2,AC、BD交于点O,AE交BD于点M,AC交BF于点N, , 交CD于点P,PQ⊥BD于点Q,连接PN, , 在不添加辅助线的情况下,请你直接写出与线段BM相等的所有线段(除线段BM外).25. 捷报电脑公司生产一批电脑,每台电脑的出厂价比成本价多1000元;若每台电脑的出厂价不变,成本价提高了12.5%,此时每台电脑仍可获利500元.(1)、求该品牌电脑的成本价和出厂价分别是多少元?(2)、频传公司在捷报电脑公司以出厂价购进一批电脑,第一个月以比出厂价提高20%的价格销售30台电脑;第二个月以第一个月销售价九折的价格,将剩余的电脑全部售完,若两个月售出电脑所获得的总利润不低于38000元,求频传公司至少购进了多少台电脑?26. 已知:BC为⊙O的弦,点A为⊙O上一点,连接AB,点K在AB上,连接CK,OK,∠AKC= 2∠ABC.
 (1)、如图1,求证:KO平分∠BKC;(2)、如图2,PA、PC为⊙O的切线,切点为点A、C,求证:;(3)、如图3,在(2)的条件下,MN是⊙O的弦, , 分别交KC、KB于点F、G,NO的延长线交PK的延长线于点E,交AB于点D,延长KO交FG于点T,若 , FN+BC=6TO, , , 求△KFG的面积.27. 在平面直角坐标系中,点O为坐标系的原点,直线AB与x轴负半轴交于点A,与y轴正半轴交于点B, , .
(1)、如图1,求证:KO平分∠BKC;(2)、如图2,PA、PC为⊙O的切线,切点为点A、C,求证:;(3)、如图3,在(2)的条件下,MN是⊙O的弦, , 分别交KC、KB于点F、G,NO的延长线交PK的延长线于点E,交AB于点D,延长KO交FG于点T,若 , FN+BC=6TO, , , 求△KFG的面积.27. 在平面直角坐标系中,点O为坐标系的原点,直线AB与x轴负半轴交于点A,与y轴正半轴交于点B, , .

 (1)、如图1,求直线AB的解析式;(2)、如图2,点D为线段AB上一点,连接OD,将线段OD绕点O顺时针旋转 , 得到线段OE,轴于点H,设 , , 求d与t的函数解析式;(3)、如图3,在(2)的条件下,点C坐标为(4,0), , 点R坐标为(16-3t,4-t),连接DR、CR, , 交射线DP于点P,于T,点G为BD中点,连接EG, , 求点E的坐标.
(1)、如图1,求直线AB的解析式;(2)、如图2,点D为线段AB上一点,连接OD,将线段OD绕点O顺时针旋转 , 得到线段OE,轴于点H,设 , , 求d与t的函数解析式;(3)、如图3,在(2)的条件下,点C坐标为(4,0), , 点R坐标为(16-3t,4-t),连接DR、CR, , 交射线DP于点P,于T,点G为BD中点,连接EG, , 求点E的坐标.