黑龙江省大庆市肇源县2022年中考第二次模拟数学试题
试卷更新日期:2022-07-13 类型:中考模拟
一、单选题
-
1. 下面的数中,比-1大的数是( )A、0 B、-1 C、-2 D、-32. 冠状病毒是一大类病毒的总称,在电子显微镜下可以观察到他们的表面有类似日冕状突起,看起来像王冠一样因此被命名为冠状病毒,其平均直径大约0.0000001米,将0.0000001用科学记数法表示为 ( )A、 B、 C、 D、3. 下列交通标志中既是中心对称图形,又是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 把分解因式,正确的是( )A、 B、 C、 D、5. 如图是一个4×4的方格,若在这个方格内投掷飞镖,则飞镖恰好落在阴影部分的概率是( )
4. 把分解因式,正确的是( )A、 B、 C、 D、5. 如图是一个4×4的方格,若在这个方格内投掷飞镖,则飞镖恰好落在阴影部分的概率是( ) A、 B、 C、 D、6. 如图所示,圆锥的底面半径为1,高为 , 则圆锥的表面积为( )
A、 B、 C、 D、6. 如图所示,圆锥的底面半径为1,高为 , 则圆锥的表面积为( ) A、π B、2π C、3π D、4π7. 下列语句中真命题有( )①点到直线的垂线段叫做点到直线的距离;②内错角相等;③两点之间线段最短;④过一点有且只有一条直线与已知直线平行;⑤在同一平面内,若两条直线都与第三条直线垂直,则这两条直线互相平行.A、5个 B、4个 C、3个 D、2个8. 如图,正方形ABCD中,点F为AB上一点,CF与BD交于点E,连接AE,若∠BCF=20°,则∠AEF的度数( )
A、π B、2π C、3π D、4π7. 下列语句中真命题有( )①点到直线的垂线段叫做点到直线的距离;②内错角相等;③两点之间线段最短;④过一点有且只有一条直线与已知直线平行;⑤在同一平面内,若两条直线都与第三条直线垂直,则这两条直线互相平行.A、5个 B、4个 C、3个 D、2个8. 如图,正方形ABCD中,点F为AB上一点,CF与BD交于点E,连接AE,若∠BCF=20°,则∠AEF的度数( )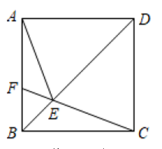 A、35° B、40° C、45° D、50°9. 古希腊数学家欧多克索斯在深入研究比例理论时,提出了分线段的“中末比”问题:点G将一线段 分为两线段 , ,使得其中较长的一段 是全长 与较短的段 的比例中项,即满足 ,后人把 这个数称为“黄金分割”数,把点G称为线段 的“黄金分割”点.如图,在 中,已知 , ,若D , E是边 的两个“黄金分割”点,则 的面积为( )
A、35° B、40° C、45° D、50°9. 古希腊数学家欧多克索斯在深入研究比例理论时,提出了分线段的“中末比”问题:点G将一线段 分为两线段 , ,使得其中较长的一段 是全长 与较短的段 的比例中项,即满足 ,后人把 这个数称为“黄金分割”数,把点G称为线段 的“黄金分割”点.如图,在 中,已知 , ,若D , E是边 的两个“黄金分割”点,则 的面积为( )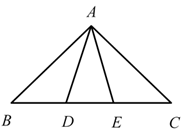 A、 B、 C、 D、10. 如图所示,已知中, , 边上的高 , 为上一点, , 交于点 , 交于点 , 设点到边的距离为 , 则的面积关于的函数图象大致为( )
A、 B、 C、 D、10. 如图所示,已知中, , 边上的高 , 为上一点, , 交于点 , 交于点 , 设点到边的距离为 , 则的面积关于的函数图象大致为( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 当x时,有意义.12. 当x=时,代数式 的值为0.13. 若点 , 则点到轴、轴的距离之和是 .14. 如图所示,已知点 , 分别是的边 , 的中点, , 相交于点 , , 则的长为 .
 15. 在平面直角坐标系 中,点 在双曲线 上.点 关于 轴的对称点 在双曲线 上,则 的值为.16. 如图,在中, , 是边上的一点, , 以为直径的与相切于点 . 若的长为 , 则阴影部分的面积为 . (结果保留)
15. 在平面直角坐标系 中,点 在双曲线 上.点 关于 轴的对称点 在双曲线 上,则 的值为.16. 如图,在中, , 是边上的一点, , 以为直径的与相切于点 . 若的长为 , 则阴影部分的面积为 . (结果保留)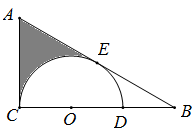 17. 明代数学家程大位的《算法统宗》中有这样一个问题(如图),其大意为:有一群人分银子,如果每人分七两,则剩余四两;如果每人分九两,则还差八两,请问:所分的银子共有两.(注:明代时1斤=16两,故有“半斤八两”这个成语)
17. 明代数学家程大位的《算法统宗》中有这样一个问题(如图),其大意为:有一群人分银子,如果每人分七两,则剩余四两;如果每人分九两,则还差八两,请问:所分的银子共有两.(注:明代时1斤=16两,故有“半斤八两”这个成语)
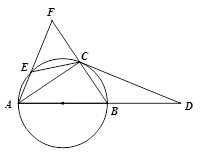
18. 如图,、 , 以为直径作 , 射线交于、两点,为弧的中点,为的中点.当射线绕点旋转时,的最小值为 .
三、解答题
-
19. 计算:20. 已知 ,求代数式 的值.21. 先化简,再求值: ,其中 .22. 如图,在大楼的正前方有一斜坡 , 米,斜坡的坡度为 , 高为 , 在斜坡下的点处测得楼顶B的仰角为 , 在斜坡上的点处测得楼顶的仰角为 , 其中在同一直线上.
 (1)、求的长度;(2)、求大楼的高度.(参考数据: , )23. 2022年6月26日—7月7日,第31届世界大学生夏季运动会将在成都举办.目前,运动会相关准备工作正在有序进行.某校体育社团随机抽查了部分同学在田径、跳水、篮球、游泳四种比赛项目中选择一种观看的意愿,并根据调查结果绘制成了两幅不完整的统计图.
(1)、求的长度;(2)、求大楼的高度.(参考数据: , )23. 2022年6月26日—7月7日,第31届世界大学生夏季运动会将在成都举办.目前,运动会相关准备工作正在有序进行.某校体育社团随机抽查了部分同学在田径、跳水、篮球、游泳四种比赛项目中选择一种观看的意愿,并根据调查结果绘制成了两幅不完整的统计图.
根据以上信息,解答下列问题:
(1)、这次被调查的同学共有人;扇形统计图中“跳水”对应的扇形圆心角的度数为;(2)、请把条形统计图补充完整;(3)、现拟从甲、乙、丙、丁四人中任选两名同学担任此次运动会的志愿者,请利用画树状图或列表的方法,求恰好选中甲、乙两名同学的概率.24. 如图,在中, , 的垂直平分线分别与 , 及的延长线相交于点 , , . 点是中点,连结并延长到 , 且 , 连接 , . (1)、试判断四边形的形状,说明理由;(2)、当时,求的长.25. 如图,矩形 的两边 的长分别为3,8,C , D在y轴上,E是 的中点,反比例函数 的图象经过点E , 与 交于点F , 且 .
(1)、试判断四边形的形状,说明理由;(2)、当时,求的长.25. 如图,矩形 的两边 的长分别为3,8,C , D在y轴上,E是 的中点,反比例函数 的图象经过点E , 与 交于点F , 且 .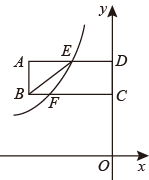 (1)、求反比例函数的解析式;(2)、在y轴上找一点P , 使得 ,求此时点P的坐标.26. 某商场准备购进A,两种型号电脑,每台A型号电脑进价比每台型号电脑多500元,用40000元购进A型号电脑的数量与用30000元购进型号电脑的数量相同,请解答下列问题:(1)、A,B型号电脑每台进价各是多少元?(2)、若每台A型号电脑售价为2500元,每台型号电脑售价为1800元,商场决定用不超过35000元同时购进A,B两种型号电脑20台,且全部售出,请写出所获的利润(单位:元)与A型号电脑(单位:台)的函数关系式并求此时的最大利润.
(1)、求反比例函数的解析式;(2)、在y轴上找一点P , 使得 ,求此时点P的坐标.26. 某商场准备购进A,两种型号电脑,每台A型号电脑进价比每台型号电脑多500元,用40000元购进A型号电脑的数量与用30000元购进型号电脑的数量相同,请解答下列问题:(1)、A,B型号电脑每台进价各是多少元?(2)、若每台A型号电脑售价为2500元,每台型号电脑售价为1800元,商场决定用不超过35000元同时购进A,B两种型号电脑20台,且全部售出,请写出所获的利润(单位:元)与A型号电脑(单位:台)的函数关系式并求此时的最大利润.