河北省石家庄市藁城区2022年中考二模数学试题
试卷更新日期:2022-07-13 类型:中考模拟
一、单选题
-
1. 如图,经过点O的直线a,b,c,d中,有一条直线与直线L垂直,请借助三角板判断,与直线L垂直的直线是( )
 A、a B、b C、c D、d2. 实数x与互为相反数,x等于( )A、2 B、-2 C、 D、3. 墨迹覆盖了等式“”中的运算符号,则覆盖的是( )A、× B、÷ C、+ D、-4. 下列变形或列式正确的是( )A、由 , 得 B、由 , 得 C、由 , 得 D、“x的平方不小于7”可表示为5. 如图,将数轴上与6两点间的线段六等分,这五个等分点所对应数依次为 . 则与相等的数是( )
A、a B、b C、c D、d2. 实数x与互为相反数,x等于( )A、2 B、-2 C、 D、3. 墨迹覆盖了等式“”中的运算符号,则覆盖的是( )A、× B、÷ C、+ D、-4. 下列变形或列式正确的是( )A、由 , 得 B、由 , 得 C、由 , 得 D、“x的平方不小于7”可表示为5. 如图,将数轴上与6两点间的线段六等分,这五个等分点所对应数依次为 . 则与相等的数是( ) A、 B、 C、 D、6. 要判断一个学生的数学考试成绩是否稳定,那么需要知道他最近连续几次数学考试成绩的( )
A、 B、 C、 D、6. 要判断一个学生的数学考试成绩是否稳定,那么需要知道他最近连续几次数学考试成绩的( )
A、平均数 B、中位数 C、众数 D、方差7. 关于x的一元二次方程(其中)的根的情况是( )A、没有实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、有没有实数根取决于a的值8. 图1和图2中所有的小正方形都全等,将图1的正方形放在图2中①②③④的某一位置,使它与原来7个小正方形组成的图形是轴对称图形,并且有两条对称轴,这个位置是( ) A、① B、② C、③ D、④9. 如图是由若干个棱长为1的小正方体搭成的一个几何体的三视图,则这个几何体的体积是( )
A、① B、② C、③ D、④9. 如图是由若干个棱长为1的小正方体搭成的一个几何体的三视图,则这个几何体的体积是( ) A、4 B、5 C、6 D、710. 如图,的对角线交于点O,直线过点O,分别交于E,F.要在BD上找点G,H,使四边形是矩形.下面给出了两种方案.
A、4 B、5 C、6 D、710. 如图,的对角线交于点O,直线过点O,分别交于E,F.要在BD上找点G,H,使四边形是矩形.下面给出了两种方案.


方案1:以O为圆心,OE为半径作圆,与BD交于G,H.
方案2:分别过E,F作的平行线,与BD交于G,H.
关于这两种方案,下面说法正确的是( )
A、方案1,2都正确 B、方案正确,方案2错误 C、方案1错误,方案2正确 D、方案1,2都错误11. 如图,六边形中,的外角都相等,即 , 分别作和的平分线交于点P,则的度数是( ) A、 B、 C、 D、12. 截至2022年4月5日,我国累计报告接种新冠疫苗接近32亿剂次,用科学记数法表示32亿是( )A、 B、 C、 D、13. 如图,在中,按以下步骤作图:
A、 B、 C、 D、12. 截至2022年4月5日,我国累计报告接种新冠疫苗接近32亿剂次,用科学记数法表示32亿是( )A、 B、 C、 D、13. 如图,在中,按以下步骤作图:
①分别以B,C为圆心,大于的长为半径作弧,两弧相交于点M,N;
②作直线交于点D,交于点E,连接 .
下列说法错误的是( )
A、 B、 C、 D、14. 如图,从笔直的公路l旁一点P出发,向西走可到达公路l上的A点;从点P出发沿与l垂直的方向走可到达点P关于公路l的对称点B点;从点P出发向正北方向走到l上,需要走的路程是( ) A、 B、 C、 D、15. 化简的结果是 , 则的值是( )A、1 B、-1 C、2 D、-216. 七巧板是中国传统数学文化的重要载体,利用七巧板可以拼出许多有趣的图案.现用图1所示的一副七巧板拼成如图2所示的六边形,若图1中七巧板的总面积为16,则图2中六边形的周长为( )
A、 B、 C、 D、15. 化简的结果是 , 则的值是( )A、1 B、-1 C、2 D、-216. 七巧板是中国传统数学文化的重要载体,利用七巧板可以拼出许多有趣的图案.现用图1所示的一副七巧板拼成如图2所示的六边形,若图1中七巧板的总面积为16,则图2中六边形的周长为( )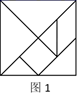
 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
17. 若的整数部分为m,小数部分为n,那么; .18. 如图,的半径是6,是的弦,C是上一点, , 点P是上一动点,则点P与点C之间的最大距离是 , 最小距离是 .
 19. 如图,平面直角坐标系中,的边在x轴上,对角线交于点M,函数的图象经过点和点M,与交于点N.则点M的坐标为 , 点N的坐标分别为 .
19. 如图,平面直角坐标系中,的边在x轴上,对角线交于点M,函数的图象经过点和点M,与交于点N.则点M的坐标为 , 点N的坐标分别为 .
三、解答题
-
20. 定义新运算: , 如 .(1)、求:的值.(2)、计算: .21. 某社区原来每天需要处理生活垃圾920吨,刚好被12个A型转运站和10个B型转运站处理.已知一个A型转运站比一个B型转运站每天多处理7吨生活垃圾.(1)、每个A型或B型转运站每天处理生活垃圾各多少吨?(2)、由于垃圾分类要求的提高,每个转运站每天将少处理8吨生活垃圾,同时由于市民环保意识增强,该社区每天需要处理的生活垃圾比原来少10吨.若该区域计划增设A型、B型转运站共5个,试问至少需要增设几个A型转运站才能当日处理完所有生活垃圾?22. 某企业为了解工人的生产能力,随机抽取了部分工人2021年6月20日每人加工零件的数量,并绘制出如下的统计图.已知该样本的平均数是19.2.

根据以上信息,解答下列问题:
(1)、样本的容量是 , 众数是 , 中位数是;若绘制成扇形统计图,每天生产20个零件的扇形部分的圆心角是;(2)、为提高工作效率,该企业欲制定工作量指标,凡超过指标者予以奖励,为使多数人获得奖励,应根据来确定工作量指标(填“平均数”,“众数”或“中位数”);(3)、已知加工零件最多的4名工人中有3名男工1名女工,要从中选两人分享经验,正好选中1名男工1名女工的概率是多少?23. 如图,的半径为3,与相切于点B,交于点C,的延长线交于点D,E是上不与B,D重合的点, . (1)、求的度数;(2)、求图中阴影部分的面积.(3)、在的延长线上取点F,使 , 作直线 , 判断直线与有怎样的位置关系,并说明理由.24. 甲、乙两人分别从A,B两地同时出发,相向而行,甲从A地骑自行车匀速去B地,中途发现丢失物品后立即原速返回寻找,经过1分钟找到了丢失物品,又立即原速赶往B地,到达B地后,立即按原路原速返回A地:乙步行匀速从B地至A地.甲、乙两人距A地的路程y(米)与时间x(分)之间的函数关系如图所示.
(1)、求的度数;(2)、求图中阴影部分的面积.(3)、在的延长线上取点F,使 , 作直线 , 判断直线与有怎样的位置关系,并说明理由.24. 甲、乙两人分别从A,B两地同时出发,相向而行,甲从A地骑自行车匀速去B地,中途发现丢失物品后立即原速返回寻找,经过1分钟找到了丢失物品,又立即原速赶往B地,到达B地后,立即按原路原速返回A地:乙步行匀速从B地至A地.甲、乙两人距A地的路程y(米)与时间x(分)之间的函数关系如图所示. (1)、甲的骑行速度为米/分,乙步行的速度是米/分.(2)、求甲返回A地时距A地的路程y(米)与时间x(分)之间的函数解析式(不必写出x的取值范围);(3)、直接写出两人每次相遇时x的值.25. 如图,函数的图象过原点,将其沿y轴翻折,得到函数的图象,把函数与的图象合并后称为函数L的图象.
(1)、甲的骑行速度为米/分,乙步行的速度是米/分.(2)、求甲返回A地时距A地的路程y(米)与时间x(分)之间的函数解析式(不必写出x的取值范围);(3)、直接写出两人每次相遇时x的值.25. 如图,函数的图象过原点,将其沿y轴翻折,得到函数的图象,把函数与的图象合并后称为函数L的图象. (1)、a的值为;函数的解析式为(注明x的取值范围);对于函数L,当函数值y随x的增大而增大时,x的取值范围是;(2)、当直线与函数L的图象有4个交点时,求b的取值范围.(3)、坐标系中有一个正方形 , 其中 , 将函数L的图象沿y轴的正方向平移m个单位,直接写出当其与正方形的边有公共点时m的最大值与最小值的差.26. 如图,是的高, , 点P是边上一动点,过点P作的平行线L,点Q是直线L上一动点,点P从点B出发,沿匀速运动,点Q从点P出发沿直线L向右匀速运动,点P运动到点A时,同时停止.设点P与点Q在同一时刻开始运动,且运动速度相同,点P的运动距离是x.
(1)、a的值为;函数的解析式为(注明x的取值范围);对于函数L,当函数值y随x的增大而增大时,x的取值范围是;(2)、当直线与函数L的图象有4个交点时,求b的取值范围.(3)、坐标系中有一个正方形 , 其中 , 将函数L的图象沿y轴的正方向平移m个单位,直接写出当其与正方形的边有公共点时m的最大值与最小值的差.26. 如图,是的高, , 点P是边上一动点,过点P作的平行线L,点Q是直线L上一动点,点P从点B出发,沿匀速运动,点Q从点P出发沿直线L向右匀速运动,点P运动到点A时,同时停止.设点P与点Q在同一时刻开始运动,且运动速度相同,点P的运动距离是x. (1)、求运动过程中,点P与点C之间的最短距离;(2)、当直线L平分的面积时,求x的值;(3)、求点Q与边的距离(用含x的式子表示);(4)、求当点Q与点C的之间的距离小于时,直接写出x的取值范围.
(1)、求运动过程中,点P与点C之间的最短距离;(2)、当直线L平分的面积时,求x的值;(3)、求点Q与边的距离(用含x的式子表示);(4)、求当点Q与点C的之间的距离小于时,直接写出x的取值范围.