河北省廊坊市安次区2022年中考一模数学试题
试卷更新日期:2022-07-13 类型:中考模拟
一、单选题
-
1. 已知 , 且 , 则( )A、 B、 C、 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 如图,数轴上表示的不等式组的解集为( )
 A、 B、 C、 D、空集4. 如图,一个由6个大小相同、棱长为1的正方体搭成的几何体,下列关于这个几何体的说法正确的是( )
A、 B、 C、 D、空集4. 如图,一个由6个大小相同、棱长为1的正方体搭成的几何体,下列关于这个几何体的说法正确的是( )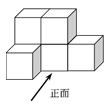 A、主视图的面积为6 B、左视图的面积为2 C、俯视图的面积为4 D、俯视图的面积为35. 如图,是的直径,弦 , 若 , 则的度数为( )
A、主视图的面积为6 B、左视图的面积为2 C、俯视图的面积为4 D、俯视图的面积为35. 如图,是的直径,弦 , 若 , 则的度数为( ) A、30° B、40° C、50° D、60°6. 根据圆规作图的痕迹,可用直尺成功地找到三角形内心的是( )A、
A、30° B、40° C、50° D、60°6. 根据圆规作图的痕迹,可用直尺成功地找到三角形内心的是( )A、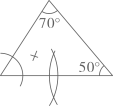 B、
B、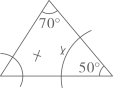 C、
C、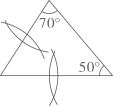 D、
D、 7. a、b为两个连续整数,若 , 则的值为( ).A、 B、 C、 D、8. 如图,一直角边长为4cm的等腰直角三角板在灯光照射下形成投影,该三角板与其投影的相似比为2∶3.则投影三角形的面积为( )
7. a、b为两个连续整数,若 , 则的值为( ).A、 B、 C、 D、8. 如图,一直角边长为4cm的等腰直角三角板在灯光照射下形成投影,该三角板与其投影的相似比为2∶3.则投影三角形的面积为( ) A、36 B、18 C、16 D、209. 如图,洋洋一家驾车从A地出发,沿着北偏东60°的方向行驶,到达B地后沿着南偏东50°的方向行驶来到C地,且C地恰好位于A地正东方向,则下列说法正确的是( )
A、36 B、18 C、16 D、209. 如图,洋洋一家驾车从A地出发,沿着北偏东60°的方向行驶,到达B地后沿着南偏东50°的方向行驶来到C地,且C地恰好位于A地正东方向,则下列说法正确的是( ) A、B地在C地的北偏西40°方向上 B、A地在B地的南偏西30°方向上 C、 D、10. 如图,矩形的顶点D在的图象的一个分支上,点和点在边上, , 连接 , 轴,则k的值为( )
A、B地在C地的北偏西40°方向上 B、A地在B地的南偏西30°方向上 C、 D、10. 如图,矩形的顶点D在的图象的一个分支上,点和点在边上, , 连接 , 轴,则k的值为( ) A、-2 B、-3 C、-4 D、11. 若关于x的方程两根异号,则a的取值范围是( )A、 B、 C、 D、12. 佳佳同学5次上学途中所花时间(单位:min)x,y,10,11,9.已知这组数据的平均数为10,方差为2,则的值为( )A、192 B、200 C、208 D、40013. 新冠病毒的直径约为 , 若用科学记数法记作 , 则n的值为( )A、5 B、6 C、7 D、814. 如图,在矩形纸片中, , , 沿对角线剪开(如图1);固定 , 把沿方向平移(如图2),当两个三角形重叠部分的面积最大时,移动的距离等于( ).
A、-2 B、-3 C、-4 D、11. 若关于x的方程两根异号,则a的取值范围是( )A、 B、 C、 D、12. 佳佳同学5次上学途中所花时间(单位:min)x,y,10,11,9.已知这组数据的平均数为10,方差为2,则的值为( )A、192 B、200 C、208 D、40013. 新冠病毒的直径约为 , 若用科学记数法记作 , 则n的值为( )A、5 B、6 C、7 D、814. 如图,在矩形纸片中, , , 沿对角线剪开(如图1);固定 , 把沿方向平移(如图2),当两个三角形重叠部分的面积最大时,移动的距离等于( ). A、1 B、1.5 C、2 D、315. 如图,在边长为5的菱形中,对角线 , 于点E,与交于点F,则的值为( )
A、1 B、1.5 C、2 D、315. 如图,在边长为5的菱形中,对角线 , 于点E,与交于点F,则的值为( ) A、 B、 C、 D、16. 如图,抛物线与直线交于A、B两点,下列是关于x的不等式或方程,结论正确的是( )
A、 B、 C、 D、16. 如图,抛物线与直线交于A、B两点,下列是关于x的不等式或方程,结论正确的是( ) A、的解集是 B、的解集是 C、的解集是 D、的解是或
A、的解集是 B、的解集是 C、的解集是 D、的解是或二、填空题
-
17. 化简: , 则n= .18. 如图,平面内将边长相等的正三角形、正方形、正五边形、正六边形的一边重合并叠在一起,则∠1、∠2、∠3三个角存在的等量关系为 .
 19. 如图,在平面直角坐标系中,点 , , , ….在x轴正半轴上,点 , , , …,在直线上.已知点 , 且 , , , …均为等边三角形.
19. 如图,在平面直角坐标系中,点 , , , ….在x轴正半轴上,点 , , , …,在直线上.已知点 , 且 , , , …均为等边三角形. (1)、线段的长度为;(2)、点的坐标为;(3)、线段的长度为 .
(1)、线段的长度为;(2)、点的坐标为;(3)、线段的长度为 .三、解答题
-
20. 已知方程的解为k,请用配方法解关于x的方程 .21. 如图,平行四边形的对角线、相交于点 , , , 连接、BF.
 (1)、求证:四边形是矩形;(2)、你所证明结论的依据是 , 该依据的逆命题是命题(填“真”或“假”).22. 如图, 的方格分为上中下三层,第一次有一枚黑色方块甲,可在方格 、 、 中移动,第二层有两枚固定不动的黑色方块,第三层有一枚黑色方块乙,可在方块 、 、 中移动,甲、乙移入方格后,四枚黑色方块构成各种拼图.
(1)、求证:四边形是矩形;(2)、你所证明结论的依据是 , 该依据的逆命题是命题(填“真”或“假”).22. 如图, 的方格分为上中下三层,第一次有一枚黑色方块甲,可在方格 、 、 中移动,第二层有两枚固定不动的黑色方块,第三层有一枚黑色方块乙,可在方块 、 、 中移动,甲、乙移入方格后,四枚黑色方块构成各种拼图. (1)、若乙固定在E处,移动甲后黑色方块构成的拼图是轴对称图形的概率是;(2)、若甲、乙均可在本层移动,用画树状图法或列表法求出黑色方块所构成拼图是中心对称图形的概率.23. 已知和都是等腰直角三角形, .
(1)、若乙固定在E处,移动甲后黑色方块构成的拼图是轴对称图形的概率是;(2)、若甲、乙均可在本层移动,用画树状图法或列表法求出黑色方块所构成拼图是中心对称图形的概率.23. 已知和都是等腰直角三角形, .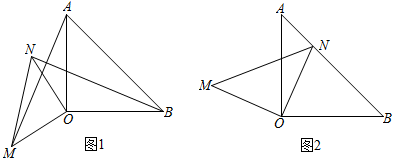 (1)、如图1,连接 , , 求证:和全等:(2)、如图2,将绕点O顺时针旋转,当点N恰好在边上时,求证: .24. 某超市一段时期内对某种商品经销情况进行统计分析:得到该商品的销售数量y(件)由基础销售量与浮动销售量两个部分组成,其中保持不变,与每件商品的售价x(元)成反比例,且市场管理局要求每件商品的售价不能超过18元销售过程中发现,当每件商品的售价定为10元时,售出34件:当每件商品的售价定为12元时,售出30件.(1)、求y与x之间的函数关系式:(2)、当该商品销售数量为40件时,求每件商品的售价;(3)、设该超市销售这种商品的总额为W,求当每件商品的售价为多少元时超市的销售总额最大?最大值是多少?
(1)、如图1,连接 , , 求证:和全等:(2)、如图2,将绕点O顺时针旋转,当点N恰好在边上时,求证: .24. 某超市一段时期内对某种商品经销情况进行统计分析:得到该商品的销售数量y(件)由基础销售量与浮动销售量两个部分组成,其中保持不变,与每件商品的售价x(元)成反比例,且市场管理局要求每件商品的售价不能超过18元销售过程中发现,当每件商品的售价定为10元时,售出34件:当每件商品的售价定为12元时,售出30件.(1)、求y与x之间的函数关系式:(2)、当该商品销售数量为40件时,求每件商品的售价;(3)、设该超市销售这种商品的总额为W,求当每件商品的售价为多少元时超市的销售总额最大?最大值是多少?

