河北省保定市易县2022年中考二模数学试题
试卷更新日期:2022-07-13 类型:中考模拟
一、单选题
-
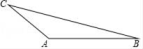
1. 在同一平面内,两条直线可能的位置关系是( )A、平行、相交或垂直 B、相交 C、平行或相交 D、平行2. 在﹣2□3的“□”中填入一个运算符号使运算结果最小( )A、+ B、﹣ C、× D、÷3. 下列等式从左到右变形,属于因式分解的是( )A、 B、 C、 D、4. 解二元一次方程组 ,把②代入①,结果正确的是( )A、 B、 C、 D、5. 下列各式从左到右的变形一定正确的是( )A、 B、 C、 D、6. (-8)5+(-8)7能被下列数整除的是( )A、5 B、6 C、7 D、97. 如图,在△ABC中,BC>AB>AC.甲、乙两人想在BC上取一点P,使得∠APC=2∠ABC,其作法如下:
(甲)作AB的中垂线,交BC于P点,则P即为所求;
(乙)以B为圆心,AB长为半径画弧,交BC于P点,则P即为所求.
对于两人的作法,下列判断何者正确?( )
 A、两人皆正确 B、两人皆错误 C、甲正确,乙错误 D、甲错误,乙正确8. 如图,货轮在航行过程中,发现灯塔在它南偏西的方向上,同时货轮在它北偏东的方向上,则此时的大小是( )
A、两人皆正确 B、两人皆错误 C、甲正确,乙错误 D、甲错误,乙正确8. 如图,货轮在航行过程中,发现灯塔在它南偏西的方向上,同时货轮在它北偏东的方向上,则此时的大小是( ) A、 B、 C、 D、9. 在①-a5·(-a)2;②(-a6)÷(-a3);③(-a2)3·(a3)2;④[-(-a)2]5中计算结果为-a10的有( )A、①② B、③④ C、②④ D、④10. 在小正方形组成网格图中,四边形 ABCD 的顶点都在格点上,如图所示.则下列结论错 误的是( )
A、 B、 C、 D、9. 在①-a5·(-a)2;②(-a6)÷(-a3);③(-a2)3·(a3)2;④[-(-a)2]5中计算结果为-a10的有( )A、①② B、③④ C、②④ D、④10. 在小正方形组成网格图中,四边形 ABCD 的顶点都在格点上,如图所示.则下列结论错 误的是( )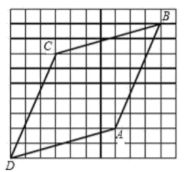 A、 B、 C、四边形是菱形 D、将边向右平移格,再向上平移格就与边重合11. 如图,数轴上、两点所对应的实数分别是、 , 若线段 , 则点所表示的实数是( )
A、 B、 C、四边形是菱形 D、将边向右平移格,再向上平移格就与边重合11. 如图,数轴上、两点所对应的实数分别是、 , 若线段 , 则点所表示的实数是( )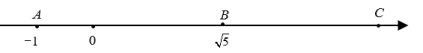 A、 B、 C、 D、12. 量角器测角度时摆放的位置如图所示,在 中,射线OC交边AB于点D,则∠ADC的度数为( )
A、 B、 C、 D、12. 量角器测角度时摆放的位置如图所示,在 中,射线OC交边AB于点D,则∠ADC的度数为( ) A、60° B、70° C、80° D、85°13. 下面是投影屏上出示的抢答题,需要回答横线上符号代表的内容,则下列回答错误的是( )
A、60° B、70° C、80° D、85°13. 下面是投影屏上出示的抢答题,需要回答横线上符号代表的内容,则下列回答错误的是( )如图,AB//CD, , 平分 , , 求的度数.
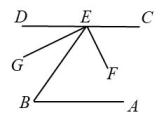
解:AB//CD,
∴ .
∵平分 .
∴■.
∵ ,
∴◆.
∴
.
∴▲.
A、※代表 B、■代表 C、◆代表 D、▲代表14. 下列判断正确的是( )A、北斗系统第五十五颗导航卫星发射前的零件检查,应选择抽样调查 B、命题“既是矩形又是菱形的四边形是正方形”是真命题 C、甲、乙两组学生身高的方差分别为S甲2=2.3,S乙2=1.8.则甲组学生的身高较整齐 D、一组数据6,5,8,7,9的中位数是815. 如图,将抛物线y=﹣x2+x+5的图象x轴上方的部分沿x轴折到x轴下方,图象的其余部分不变,得到一个新图象.则新图象与直线y=﹣5的交点个数为( )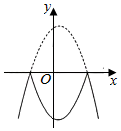 A、1 B、2 C、3 D、416. 如图,东汉末年数学家刘徽利用青朱出入图,证明了勾股定理,“勾自乘为朱方,股自乘为青方,令出入相补,各从其类”.若CE=4,DE=2,则正方形BFGH的面积为( )
A、1 B、2 C、3 D、416. 如图,东汉末年数学家刘徽利用青朱出入图,证明了勾股定理,“勾自乘为朱方,股自乘为青方,令出入相补,各从其类”.若CE=4,DE=2,则正方形BFGH的面积为( )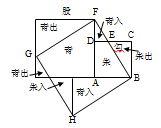 A、15 B、25 C、100 D、117
A、15 B、25 C、100 D、117二、填空题
-
17. 一个数的平方根是a+4和2a+5,则a= , 这个正数是 .18. 已知有甲、乙两个长方形,它们的边长如图所示(m为正整数),甲、乙的面积分别为S1 , S2 .
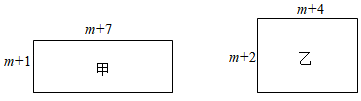 (1)、S1与S2的大小关系为:S1S2;(用“>”、“<”、“=”填空)(2)、若满足条件|S1﹣S2|<n≤2021的整数n有且只有4个,则m的值为 .19. 如图,在平面直角坐标系xOy中,点A与点B的坐标分别是(1,0)与(7,0).对于坐标平面内的一动点P,给出如下定义:若∠APB=45°,则称点P为线段AB的“等角点.”
(1)、S1与S2的大小关系为:S1S2;(用“>”、“<”、“=”填空)(2)、若满足条件|S1﹣S2|<n≤2021的整数n有且只有4个,则m的值为 .19. 如图,在平面直角坐标系xOy中,点A与点B的坐标分别是(1,0)与(7,0).对于坐标平面内的一动点P,给出如下定义:若∠APB=45°,则称点P为线段AB的“等角点.”①若点P为线段AB在第一象限的“等角点”,且在直线x=4上,则点P的坐标为 ;
②若点P为线段AB的“等角点”,并且在y轴上,则点P的坐标为 .
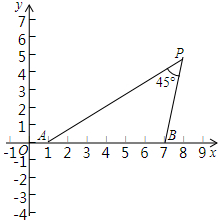
三、解答题
-
20. 先计算,再阅读材料,解决问题:(1)、计算: .(2)、认真阅读材料,解决问题:
计算: .
分析:利用通分计算 的结果很麻烦,可以采用以下方法进行计算:
解:原式的倒数是:
.
故原式 .
请你根据对所提供材料的理解,选择合适的方法计算: .
21. A、B、C、D四个车站的位置如图所示,A、B两站之间的距离AB=a-b,B、C两站之间的距离BC=2a-b,B、D两站之间的距离BD=a-2b-1.求: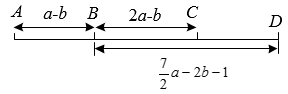 (1)、A、C两站之间的距离AC;(2)、若A、C两站之间的距离AC=90km,求C、D两站之间的距离CD.22. 某校为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中只选出一类最喜爱的电视节目,以下是根据调查结果绘制的统计图表的一部分.
(1)、A、C两站之间的距离AC;(2)、若A、C两站之间的距离AC=90km,求C、D两站之间的距离CD.22. 某校为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中只选出一类最喜爱的电视节目,以下是根据调查结果绘制的统计图表的一部分.类别
A
B
C
D
E
节目类型
新闻
体育
动画
娱乐
戏曲
人数
12
30
m
54
9
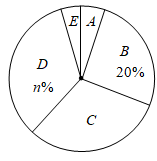
请你根据以上的信息,回答下列问题:
(1)、被调查学生的总数为人,统计表中m的值为 , 统计图中n的值为;(2)、在统计图中,E类所对应扇形的圆心角的度数为;(3)、喜爱体育电视节目的学生中有4人(甲、乙、丙、丁)在学校参加体育训练,现要从4个人中选拔两人代表参加市运动会,求出甲丙同时被选中的概率是多少.(用列表法或树状图法求概率)23. 甲骑车从A地到B地,乙骑车从B地到A地,甲的速度小于乙的速度,两人同时出发,沿同一条道路骑行,图中的折线表示两人之间的距离y(km)与甲的行驶时间x(h)之间的关系,根据图象回答下列问题: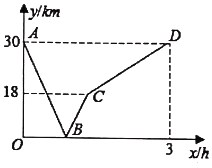 (1)、甲骑完全程用时小时;甲的速度是km/h;(2)、求甲、乙相遇的时间;(3)、求甲出发多长时间两人相距10千米.24. 如图,以矩形ABCD的边CD为直径作⊙O,点E是AB 的中点,连接CE交⊙O于点F,连接AF并延长交BC于点H.
(1)、甲骑完全程用时小时;甲的速度是km/h;(2)、求甲、乙相遇的时间;(3)、求甲出发多长时间两人相距10千米.24. 如图,以矩形ABCD的边CD为直径作⊙O,点E是AB 的中点,连接CE交⊙O于点F,连接AF并延长交BC于点H. (1)、若连接AO,试判断四边形AECO的形状,并说明理由;(2)、求证:AH是⊙O的切线;(3)、若AB=6,CH=2,则AH的长为.25. 某花卉市场店铺老板用5400元按批发价购买了一批花卉.若将批发价降低 , 则可以多购买该花卉20盆.据市场调查反映,该花卉每盆售价42元时,每天可卖出20盆;若调整价格,每盆花卉每涨价2元,每天要少卖出1盆.(1)、该花卉每盆批发价是多少元?(2)、店铺老板决定在每盆售价42元的基础上,每盆花卉涨价不超过10元,问该花卉一天最大的销售利润是多少元?(3)、该店铺开展快递托运送货到家活动,但每盆花卉店铺还需增加a元的快递成本,若每盆花卉售价不低于62元时,每天的利润将随着售价的增长不断降低,请直接写出快递成本最多是多少元?26. 几何探究:
(1)、若连接AO,试判断四边形AECO的形状,并说明理由;(2)、求证:AH是⊙O的切线;(3)、若AB=6,CH=2,则AH的长为.25. 某花卉市场店铺老板用5400元按批发价购买了一批花卉.若将批发价降低 , 则可以多购买该花卉20盆.据市场调查反映,该花卉每盆售价42元时,每天可卖出20盆;若调整价格,每盆花卉每涨价2元,每天要少卖出1盆.(1)、该花卉每盆批发价是多少元?(2)、店铺老板决定在每盆售价42元的基础上,每盆花卉涨价不超过10元,问该花卉一天最大的销售利润是多少元?(3)、该店铺开展快递托运送货到家活动,但每盆花卉店铺还需增加a元的快递成本,若每盆花卉售价不低于62元时,每天的利润将随着售价的增长不断降低,请直接写出快递成本最多是多少元?26. 几何探究: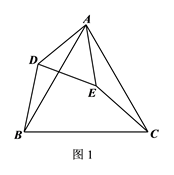

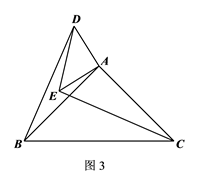 (1)、(问题发现)如图1所示,△ABC和△ADE是有公共顶点的等边三角形,BD、CE的关系是(选填“相等”或“不相等”);(请直接写出答案)(2)、(类比探究)如图2所示,△ABC和△ADE是有公共顶点的含有 角的直角三角形,(1)中的结论还成立吗?请说明理由;(3)、(拓展延伸)如图3所示,△ADE和△ABC是有公共顶点且相似比为1 : 2的两个等腰直角三角形,将△ADE绕点A自由旋转,若 ,当B、D、E三点共线时,直接写出BD的长.
(1)、(问题发现)如图1所示,△ABC和△ADE是有公共顶点的等边三角形,BD、CE的关系是(选填“相等”或“不相等”);(请直接写出答案)(2)、(类比探究)如图2所示,△ABC和△ADE是有公共顶点的含有 角的直角三角形,(1)中的结论还成立吗?请说明理由;(3)、(拓展延伸)如图3所示,△ADE和△ABC是有公共顶点且相似比为1 : 2的两个等腰直角三角形,将△ADE绕点A自由旋转,若 ,当B、D、E三点共线时,直接写出BD的长.