河北省保定市竞秀区2022年中考二模数学试题
试卷更新日期:2022-07-13 类型:中考模拟
一、单选题
-
1.
如图是某个几何体的三视图,该几何体是( )
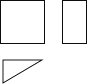 A、圆锥 B、三棱锥 C、圆柱 D、三棱柱2. 已知 , 则a的倒数是( )A、 B、 C、 D、3. 从“+,-,×,÷”中选择一种运算符号,填入算式“”的“□”中,使其运算结果为有理数,则应选择的运算符号是( )A、+ B、- C、× D、÷4. 在物联网时代的所有芯片中,芯片已成为需求的焦点.已知 . 下面将用科学记数法表示正确的是( )A、 B、 C、 D、5. 如图,天平右盘中的每个砝码的质量为10g,则物体M的质量m(g)的取值范围在数轴上可表示为( )
A、圆锥 B、三棱锥 C、圆柱 D、三棱柱2. 已知 , 则a的倒数是( )A、 B、 C、 D、3. 从“+,-,×,÷”中选择一种运算符号,填入算式“”的“□”中,使其运算结果为有理数,则应选择的运算符号是( )A、+ B、- C、× D、÷4. 在物联网时代的所有芯片中,芯片已成为需求的焦点.已知 . 下面将用科学记数法表示正确的是( )A、 B、 C、 D、5. 如图,天平右盘中的每个砝码的质量为10g,则物体M的质量m(g)的取值范围在数轴上可表示为( ) A、
A、 B、
B、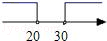 C、
C、 D、
D、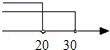 6. 一定相等的一组是( )A、与 B、与 C、与 D、与27. 一组数据2、3、5、x、7、4、6、9的唯一众数是5,则这组数据的中位数是( )A、4 B、4.5 C、5 D、5.58. 若 , 那么( )A、k=-8,从左到右是乘法运算 B、k=8,从左到右是乘法运算 C、k=-8,从左到右是因式分解 D、k=8,从左到右是因式分解9. 嘉嘉和淇淇下棋,嘉嘉执圆子,淇淇执方子.棋盘中心方子的位置用(1,0)表示,右下角方子的位置用(2,-1)表示.嘉嘉将第4枚圆子放入棋盘后,所有棋子构成一个轴对称图形.则嘉嘉放的位置是( )
6. 一定相等的一组是( )A、与 B、与 C、与 D、与27. 一组数据2、3、5、x、7、4、6、9的唯一众数是5,则这组数据的中位数是( )A、4 B、4.5 C、5 D、5.58. 若 , 那么( )A、k=-8,从左到右是乘法运算 B、k=8,从左到右是乘法运算 C、k=-8,从左到右是因式分解 D、k=8,从左到右是因式分解9. 嘉嘉和淇淇下棋,嘉嘉执圆子,淇淇执方子.棋盘中心方子的位置用(1,0)表示,右下角方子的位置用(2,-1)表示.嘉嘉将第4枚圆子放入棋盘后,所有棋子构成一个轴对称图形.则嘉嘉放的位置是( ) A、(1,2) B、(1,1) C、(-1,1) D、(-2,1)10. 如图,在 中, 平分 ,使用尺规作射线 ,与 交于点 ,下列判断正确的是( )
A、(1,2) B、(1,1) C、(-1,1) D、(-2,1)10. 如图,在 中, 平分 ,使用尺规作射线 ,与 交于点 ,下列判断正确的是( ) A、 平分 B、 C、点 是 的内心 D、点 到点 , , 的距离相等11. 有三个角是直角的四边形是矩形.
A、 平分 B、 C、点 是 的内心 D、点 到点 , , 的距离相等11. 有三个角是直角的四边形是矩形.已知:如图, .
求证:四边形是矩形.

证明:∵ ,
∴ , ,
∴ , (①),
∵ ,
∴四边形是矩形(②),
在证明过程中,依据①、②分别表示( )
A、①表示同旁内角互补,两直线平行;②表示对角线相等的平行四边形是矩形 B、①表示同旁内角互补,两直线平行;②表示有一个角是直角的平行四边形是矩形 C、①表示两直线平行,同旁内角互补;②表示有一个角是直角的平行四边形是矩形 D、①表示两直线平行,同旁内角互补;②表示对角线相等的平行四边形是矩形12. 某市积极响应国家的号召“房子是用来住的,不是用来炒的”,在宏观调控下,商品房成交价由今年1月份的每平方米10000元下降到3月份的每平方米8100元,且今年房价在2月份、3月份、4月份的下降率保持一致,则4月份的房价单价为每平方米( ).A、7300元 B、7290元 C、7280元 D、7270元13. 如图为三角形纸片ABC,其中D点和E点将AB三等分,F点为DE中点.若小慕从AB上的一点P,沿着与直线BC平行的方向将纸片剪开后,剪下的小三角形纸片面积为△ABC的 , 则下列关于P点位置的叙述正确的是( ) A、在FE上,但不与F点也不与E点重合 B、在DF上,但不与D点也不与F点重合 C、与E点重合 D、与D点重合14. 有甲,乙两块边长为a米(a>8)的正方形试验田.负责试验田的杨师傅将试验田的形状进行了调整(如图):沿甲试验田的一边在试验田内修了1米宽的水池,又在邻边增加了1米宽的田地;沿乙试验田的一组邻边在试验田内均修了1米宽的小路.杨师傅在调整后的试验田上种植了某种小麦,其中甲试验田收获了200千克小麦,乙试验田收获了150千克小麦,对于这两块试验田的单位面积产量,下列说法正确的是( )
A、在FE上,但不与F点也不与E点重合 B、在DF上,但不与D点也不与F点重合 C、与E点重合 D、与D点重合14. 有甲,乙两块边长为a米(a>8)的正方形试验田.负责试验田的杨师傅将试验田的形状进行了调整(如图):沿甲试验田的一边在试验田内修了1米宽的水池,又在邻边增加了1米宽的田地;沿乙试验田的一组邻边在试验田内均修了1米宽的小路.杨师傅在调整后的试验田上种植了某种小麦,其中甲试验田收获了200千克小麦,乙试验田收获了150千克小麦,对于这两块试验田的单位面积产量,下列说法正确的是( ) A、甲试验田的单位面积产量高 B、乙试验田的单位面积产量高 C、两块试验田的单位面积产量一样 D、无法判断哪块试验田的单位面积产量高15. 某限高曲臂道路闸口如图所示,垂直地面于点 , 与水平线的夹角为 , , 若米,米,车辆的高度为(单位:米),不考虑闸口与车辆的宽度:
A、甲试验田的单位面积产量高 B、乙试验田的单位面积产量高 C、两块试验田的单位面积产量一样 D、无法判断哪块试验田的单位面积产量高15. 某限高曲臂道路闸口如图所示,垂直地面于点 , 与水平线的夹角为 , , 若米,米,车辆的高度为(单位:米),不考虑闸口与车辆的宽度:①当时,小于3.4米的车辆均可以通过该闸口;②当时,等于3.0米的车辆不可以通过该闸口;③当时,等于3.2米的车辆可以通过该闸口.

上述说法正确的个数为( )
A、0个 B、1个 C、2个 D、3个16. 现有一张纸片,∠BAF=∠B=∠C=∠D=∠FED=∠F=90°,AB=AF=2,EF=ED=1.有甲、乙两种剪拼方案,如图1,2所示将它们沿着虚线剪开后,各自要拼一个与原来面积相等的正方形,则( ) A、甲、乙都可以 B、甲、乙都不可以 C、甲不可以、乙可以 D、甲可以、乙不可以
A、甲、乙都可以 B、甲、乙都不可以 C、甲不可以、乙可以 D、甲可以、乙不可以二、填空题
-
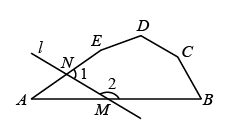
17. 计算: .18. 如图,在五边形中, , 去掉后得到一个六边形 , 则的度数为 .
 19. 如图,在平面直角坐标系中,矩形的顶点 , 分别在轴,轴的正半轴上,点 , 是的两个三等分点,过点 , 作轴的平行线分别交于点 , , 反比例函数的图象经过点 , 分别交 , 于点 , , 分别过点 , , 作轴的垂线,垂足分别为 , . 图中阴影部分的面积分别为 , , .
19. 如图,在平面直角坐标系中,矩形的顶点 , 分别在轴,轴的正半轴上,点 , 是的两个三等分点,过点 , 作轴的平行线分别交于点 , , 反比例函数的图象经过点 , 分别交 , 于点 , , 分别过点 , , 作轴的垂线,垂足分别为 , . 图中阴影部分的面积分别为 , , . (1)、若点的坐标为 , 则;(2)、若 , 则点的坐标为;(3)、若 , 则= .
(1)、若点的坐标为 , 则;(2)、若 , 则点的坐标为;(3)、若 , 则= .三、解答题
-
20. 已知数轴上有两个点A:-3,B:1.
 (1)、求线段AB的长;(2)、若 , 且m<0;在点B右侧且到点B距离为5的点表示的数为n.
(1)、求线段AB的长;(2)、若 , 且m<0;在点B右侧且到点B距离为5的点表示的数为n.①求m与n;
②计算2m+n+mn;
21. 已知两个整式 , B=■x+1,其中系数■被污染.(1)、若■是2,化简A-B;(2)、若x=1时,A-B的值为2.说明原题中■是几?22. 如图是三个从外观看毫无差别的鸡蛋,其中有两个是熟鸡蛋,一个是生鸡蛋. (1)、随机取出一个是熟鸡蛋的概率是 , 要使随机取出一个熟鸡蛋的概率为 , 则应在其中添加个生鸡蛋;(2)、若从中随机取出两个鸡蛋,请用画树状图或列表的方法求正好是两个熟鸡蛋的概率.23. 如图,中, , 将绕点逆时针旋转得到 . 与交于点 , 分别交、于点、 .
(1)、随机取出一个是熟鸡蛋的概率是 , 要使随机取出一个熟鸡蛋的概率为 , 则应在其中添加个生鸡蛋;(2)、若从中随机取出两个鸡蛋,请用画树状图或列表的方法求正好是两个熟鸡蛋的概率.23. 如图,中, , 将绕点逆时针旋转得到 . 与交于点 , 分别交、于点、 . (1)、与的数量关系是:;(2)、求证:;(3)、当 , , 三点共线时,恰好 , 求此时的长.24. A,B,C三地在同一条公路上,C地在A,B两地之间,且到A,B两地的路程相等.甲、乙两车分别从A,B两地同时出发,匀速行驶.甲车到达C地并停留1小时后以原速继续前往B地,到达B地后立即调头(调头时间忽略不计),并按原路原速返回,到达C地停止行驶;乙车经C地到达A地停止行驶.在两车行驶的过程中,甲、乙两车距C地的路程y(单位:千米)与甲车所用时间x(单位:小时)之间的函数图象如图所示,请结合图象信息解答下列问题:
(1)、与的数量关系是:;(2)、求证:;(3)、当 , , 三点共线时,恰好 , 求此时的长.24. A,B,C三地在同一条公路上,C地在A,B两地之间,且到A,B两地的路程相等.甲、乙两车分别从A,B两地同时出发,匀速行驶.甲车到达C地并停留1小时后以原速继续前往B地,到达B地后立即调头(调头时间忽略不计),并按原路原速返回,到达C地停止行驶;乙车经C地到达A地停止行驶.在两车行驶的过程中,甲、乙两车距C地的路程y(单位:千米)与甲车所用时间x(单位:小时)之间的函数图象如图所示,请结合图象信息解答下列问题: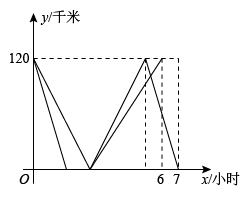 (1)、乙车的速度为千米/时;(2)、求乙车从C地到A地的过程中,y与x的函数关系式(不用写自变量的取值范围);(3)、请直接写出x为何值时两车距C地的路程之和为120千米?25. 如图,抛物线与轴交于 , 两点,其中 . 点为该抛物线上一点.
(1)、乙车的速度为千米/时;(2)、求乙车从C地到A地的过程中,y与x的函数关系式(不用写自变量的取值范围);(3)、请直接写出x为何值时两车距C地的路程之和为120千米?25. 如图,抛物线与轴交于 , 两点,其中 . 点为该抛物线上一点. (1)、点坐标为;(2)、直线交直线于点 , 交抛物线于点 , 且点在点上方,连接、;
(1)、点坐标为;(2)、直线交直线于点 , 交抛物线于点 , 且点在点上方,连接、;①请直接写出线段长(用含的代数式表示) ▲ ;
②求面积的最大值.
(3)、将直线绕点逆时针旋转得到直线 , 若点是直线上的点,且 , 请直接写出点坐标 .26. 如图,平行四边形中,于 , , , 经过点作圆和边切于点(点可与点、重合),分别交边,边于点、 . (1)、的长为;(2)、若点在边上,求的长;(3)、嘉琪说:“若点与点重合,则点一定在圆上”.你觉得嘉琪的判断对吗?请说明理由;(4)、设圆的半径为 , 直接写出的取值范围.
(1)、的长为;(2)、若点在边上,求的长;(3)、嘉琪说:“若点与点重合,则点一定在圆上”.你觉得嘉琪的判断对吗?请说明理由;(4)、设圆的半径为 , 直接写出的取值范围.