北京市昌平区2022年中考数学二模试题

试卷更新日期：2022-07-13 类型：中考模拟

进入出卷网下载

一、单选题

1. 斗笠，又名箬笠，即以竹皮编织的用来遮光遮雨的帽子，可以看做一个圆锥，下列平面展开图中能围成一个圆锥的是（）

A、 B、 C、 D、

查看试题解析
2. 2021年12月9日15时40分，“天宫课堂”第一课开始，神舟十三号乘组航天员翟志刚、王亚平、叶光富在中国空间站进行太空授课，全国超过6000万中小学生观看授课直播，其中6000万用科学记数法表示为（）

A、6000×10⁴ B、6×10⁷ C、0.6×10⁸ D、6×10⁸

查看试题解析
3. 第24届冬季奥林匹克运动会于2022年2月4日在北京开幕.2022年北京冬奥会会徽以汉字“冬”为灵感来源；北京冬奥会的吉祥物“冰墩墩”是以熊猫为原型进行设计创作；北京冬季残奥会的吉祥物“雪容融”是以灯笼为原型进行设计创作．下列冬奥元素图片中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 若实数a，b在数轴上的对应点的位置如图所示，则以下结论正确的是（）

A、 $| a | < | b |$ B、 $a b > 0$ C、 $a < - b$ D、 $a - b > 0$

查看试题解析
5. 若 $a + b = 1$ ，则代数式 $(\frac{a}{b} - 1) \cdot \frac{b}{a^{2} - b^{2}}$ 的值为（）

A、-2 B、-1 C、1 D、2

查看试题解析
6. 一个不透明的盒子中装有15个除颜色外无其他差别的小球，其中有2个黄球和3个绿球，其余都是红球，从中随机摸出一个小球，恰好是红球的概率为（）

A、 $\frac{2}{15}$ B、 $\frac{1}{5}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看试题解析
7. 如图， $⊙ O$ 的直径 $A B ⊥ C D$ ，垂足为 $E$ ， $∠ A = 30 °$ ，连接 $C O$ 并延长交 $⊙ O$ 于点 $F$ ，连接 $F D$ ，则 $∠ C F D$ 的度数为（）

A、 $30 °$ B、 $45 °$ C、 $60 °$ D、 $75 °$

查看试题解析
8. 某气球内充满了一定质量的气体，当温度不变时，气球内气体的气压 $P$ （单位：千帕）随气球内气体的体积 $V$ （单位：立方米）的变化而变化， $P$ 随 $V$ 的变化情况如下表所示，那么在这个温度下，气球内气体的气压P与气球内气体的体积 $V$ 的函数关系最可能是
$V$ （单位：立方米）
64
48
38.4
32
24
…
$P$ （单位：千帕）
1.5
2
2.5
3
4
…

A、正比例函数 B、一次函数 C、二次函数 D、反比例函数

查看试题解析

二、填空题

9. 若分式 $\frac{1}{x - 5}$ 有意义，则实数x的取值范围是．

查看试题解析
10. 因式分解： $3 x^{2} - 6 x + 3 =$ ．

查看试题解析
11. 正多边形一个外角的度数是 $60^{\circ}$ ，则该正多边形的边数是.

查看试题解析
12. 如图，在平面直角坐标系 $x O y$ 中，直线 $y = 3 x$ 与双曲线 $y = \frac{m}{x} (m \neq 0)$ 交于 $A$ ， $B$ 两点，若点 $A$ ， $B$ 的横坐标分别为 $x_{1}$ ， $x_{2}$ ，则 $x_{1} + x_{2} =$ ．

查看试题解析
13. 方程术是《九章算术》最高的数学成就，其中“盈不足”一章中曾记载“今有大器五小器一容三斛(“斛”是古代的一种容量单位)，大器一小器五容二斛，问大小器各容几何？”

译文：有大小两种盛酒的桶，已知5个大桶加上1个小桶可以盛酒3斛，1个大桶加上5个小桶可以盛酒2斛，问1个大桶和1个小桶分别可以盛酒多少斛？

设1个大桶可以盛酒 $x$ 斛，1个小桶可以盛酒 $y$ 斛，依题意，可列二元一次方程组为．

查看试题解析
14. 不等式组 ${\begin{array}{l} 2 (x + 1) \leq 3 \\ \frac{x - 2}{3} > - 1 \end{array}$ 的解集为．

查看试题解析
15. 如图，在平面直角坐标系 $x O y$ 中，点 $A (1 ， 0)$ ， $B (0 ， 2)$ ．将线段 $A B$ 绕点 $A$ 顺时针旋转 $90 °$ 得到线段 $A C$ ，则点 $C$ 的坐标为．

查看试题解析
16. 下图是国家统计局发布的2021年2月至2022年2月北京居民消费价格涨跌幅情况折线图（注：2022年2月与2021年2月相比较称为同比，2022年2月与2022年1月相比较称为环比）．
根据图中信息，有下面四个推断：
①2021年2月至2022年2月北京居民消费价格同比均上涨；
②2021年2月至2022年2月北京居民消费价格环比有涨有跌；
③在北京居民消费价格同比数据中，2021年4月至8月的同比数据的方差小于2021年9月至2022年1月同比数据的方差；
④在北京居民消费价格环比数据中，2021年4月至8月的环比数据的平均数小于2021年9月至2022年1月环比数据的平均数．
所有合理推断的序号是．

查看试题解析

三、解答题

17. 计算： ${(1 - \sqrt{3})}^{0} + | - \sqrt{2} | - 2 cos 45 ° + {(\frac{1}{4})}^{- 1}$

查看试题解析
18. 解方程： $\frac{3 x}{x - 2} = 1 - \frac{2}{x - 2}$ .

查看试题解析
19. 已知：如图， $∠ M O N$ ．
求作： $∠ B A D$ ，使 $∠ B A D = ∠ M O N$ ．
下面是小明设计的尺规作图过程．
作法：
①在 $O M$ 上取一点 $A$ ，以 $A$ 为圆心， $O A$ 为半径画弧，交射线 $O A$ 于点 $B$ ；
②在射线 $O N$ 上任取一点 $C$ ，连接 $B C$ ，分别以 $B$ ， $C$ 为圆心，大于 $\frac{1}{2} B C$ 为半径画弧，两弧交于点 $E$ ， $F$ ，作直线 $E F$ ，与 $B C$ 交于点 $D$ ；
③作射线 $A D$ ， $∠ B A D$ 即为所求．

(1)、使用直尺和圆规，补全图形（保留作图痕迹）；

(2)、完成下列证明．
证明：∵ $E F$ 垂直平分 $B C$ ，
∴ ▲ $= D C$ ．
∵ $A O = A B$ ，
∴ $A D ∥ O C$ （）（填推理依据）．
∴ $∠ B A D = ∠ M O N$ ．

查看试题解析
20. 已知关于 $x$ 的一元二次方程 $x^{2} + 4 x + k = 0$ 有两个不相等的实数根，写出一个满足条件 $k$ 的值，并求此时方程的根．

查看试题解析
21. 如图，在矩形 $A B C D$ 中，对角线 $A C$ ， $B D$ 交于点 $O$ ，分别过点 $C$ ， $D$ 作 $B D$ ， $A C$ 的平行线交于点 $E$ ，连接 $O E$ 交 $A D$ 于点 $F$ ．

(1)、求证：四边形 $O C E D$ 是菱形；

(2)、若 $A C = 8$ ， $∠ D O C = 60 °$ ，求菱形 $O C E D$ 的面积．

查看试题解析
22. 在平面直角坐标系 $x O y$ 中，直线 $y = k x + b (k \neq 0)$ 与直线 $y = x$ 平行，且过点 $(2 ， 1)$ ．

(1)、求这个一次函数的解析式；

(2)、直线 $y = k x + b (k \neq 0)$ 分别交 $x$ ， $y$ 轴于点A，点 $B$ ，若点 $C$ 为 $x$ 轴上一点，且 $S_{△ A B C} = 2$ ，直接写出点 $C$ 的坐标．

查看试题解析
23. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ， $B C$ ， $A C$ 与 $⊙ O$ 交于点 $F$ ， $D$ ， $B E$ 为 $⊙ O$ 直径，点 $E$ 在 $A B$ 上，连接 $B D$ ， $D E$ ， $∠ A D E = ∠ D B E$ ．

(1)、求证： $A C$ 是 $⊙ O$ 的切线；

(2)、若 $s i n A = \frac{3}{5}$ ， $⊙ O$ 的半径为3，求 $B C$ 的长．

查看试题解析
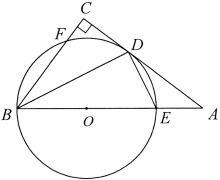24. 如图，在一次学校组织的社会实践活动中，小龙看到农田上安装了很多灌溉喷枪，喷枪喷出的水流轨迹是抛物线，他发现这种喷枪射程是可调节的，且喷射的水流越高射程越远，于是他从该农田的技术部门得到了这种喷枪的一个数据表，水流的最高点与喷枪的水平距离记为 $x$ ，水流的最高点到地面的距离记为 $y$ ．
$y$ 与 $x$ 的几组对应值如下表：
$x$ （单位： $m$ ）
0
$\frac{1}{2}$
1
$\frac{3}{2}$
2
$\frac{5}{2}$
3
4
…
$y$ （单位： $m$ ）
1
$\frac{9}{8}$
$\frac{5}{4}$
$\frac{11}{8}$
$\frac{3}{2}$
$\frac{13}{8}$
$\frac{7}{4}$
2
…

(1)、该喷枪的出水口到地面的距离为m；

(2)、在平面直角坐标系 $x O y$ 中，描出表中各组数值所对应的点，并画出 $y$ 与 $x$ 的函数图象；

(3)、结合（2）中的图像，估算当水流的最高点与喷枪的水平距离为 $8 m$ 时，水流的最高点到地面的距离为 $m$ （精确到 $1 m$ ）．根据估算结果，计算此时水流的射程约为 $m$ （精确到 $1 m$ ）

查看试题解析
25. 甲，乙两个小区各有300户居民，为了解两个小区3月份用户使用燃气量情况，小明和小丽分别从中随机抽取30户进行调查，并对数据进行整理、描述和分析．下面给出了部分信息．
a．甲小区用气量频数分布直方图如下（数据分成5组： $5 \leq x < 10$ ， $10 \leq x < 15$ ， $15 \leq x < 20$ ， $20 \leq x < 25$ ， $25 \leq x < 30$ ）
b．甲小区用气量的数据在 $15 \leq x < 20$ 这一组的是：
15 15 16 16 16 16 18 18 18 18 18 19
c．甲，乙两小区用气量的平均数、中位数、众数如下：
小区
平均数
中位数
众数
甲
17.2
$m$
18
乙
17.7
19
15
根据以上信息，回答下列问题：

(1)、写出表中 $m$ 的值；

(2)、在甲小区抽取的用户中，记3月份用气量高于它们的平均用气量的户数为 $p_{1}$ ．在乙小区抽取的用户中，记3月份用气量高于它们的平均用气量的户数为 $p_{2}$ ．比较 $p_{1}$ ， $p_{2}$ 的大小，并说明理由；

(3)、估计甲小区中用气量超过15立方米的户数．

查看试题解析
26. 在平面直角坐标系 $x O y$ 中，已知抛物线 $y = a x^{2} + b x - 1 (a > 0)$ ．

(1)、若抛物线过点 $(4 ， - 1)$ ．
①求抛物线的对称轴；
②当 $- 1 < x < 0$ 时，图像在 $x$ 轴的下方，当 $5 < x < 6$ 时，图像在 $x$ 轴的上方，在平面直角坐标系中画出符合条件的图像，求出这个抛物线的表达式；

(2)、若 $(- 4 ， y_{1})$ ， $(- 2 ， y_{2})$ ， $(1 ， y_{3})$ 为抛物线上的三点且 $y_{3} > y_{1} > y_{2}$ ，设抛物线的对称轴为直线 $x = t$ ，直接写出 $t$ 的取值范围．

查看试题解析
27. 如图，已知 $∠ M O N = α (0 ° < α < 90 °)$ ， $O P$ 是 $∠ M O N$ 的平分线，点A是射线 $O M$ 上一点，点A关于 $O P$ 对称点 $B$ 在射线 $O N$ 上，连接 $A B$ 交 $O P$ 于点 $C$ ，过点A作 $O N$ 的垂线，分别交 $O P$ ， $O N$ 于点 $D$ ， $E$ ，作 $∠ O A E$ 的平分线 $A Q$ ，射线 $A Q$ 与 $O P$ ， $O N$ 分别交于点 $F$ ， $G$ ．

(1)、①依题意补全图形；
②求 $∠ B A E$ 度数；（用含 $α$ 的式子表示）

(2)、写出一个 $α$ 的值，使得对于射线 $O M$ 上任意的点A总有 $O D = \sqrt{2} A F$ （点A不与点 $O$ 重合），并证明．

查看试题解析
28. 在平面直角坐标系 $x O y$ 中， $⊙ O$ 的半径为1，对于 $△ A B C$ 和直线 $l$ 给出如下定义：若 $△ A B C$ 的一条边关于直线 $l$ 的对称线段 $P Q$ 是 $⊙ O$ 的弦，则称 $△ A B C$ 是 $⊙ O$ 的关于直线 $l$ 的“关联三角形”，直线 $l$ 是“关联轴”．

(1)、如图1，若 $△ A B C$ 是 $⊙ O$ 的关于直线 $l$ 的“关联三角形”，请画出 $△ A B C$ 与 $⊙ O$ 的“关联轴”（至少画两条）；

(2)、若 $△ A B C$ 中，点 $A$ 坐标为 $(2 ， 3)$ ，点 $B$ 坐标为 $(4 ， 1)$ ，点 $C$ 在直线 $y = - x + 3$ 的图像上，存在“关联轴 $l$ ”使 $△ A B C$ 是 $⊙ O$ 的关联三角形，求点 $C$ 横坐标的取值范围；

(3)、已知 $A (\sqrt{3} ， 1)$ ，将点 $A$ 向上平移2个单位得到点 $M$ ，以 $M$ 为圆心 $M A$ 为半径画圆， $B$ ， $C$ 为 $⊙ M$ 上的两点，且 $A B = 2$ （点 $B$ 在点 $A$ 右侧），若 $△ A B C$ 与 $⊙ O$ 的关联轴至少有两条，直接写出 $O C$ 的最小值和最大值，以及 $O C$ 最大时 $A C$ 的长．

查看试题解析

$V$ （单位：立方米）	64	48	38.4	32	24	…
$P$ （单位：千帕）	1.5	2	2.5	3	4	…

$x$ （单位： $m$ ）	0	$\frac{1}{2}$	1	$\frac{3}{2}$	2	$\frac{5}{2}$	3	4	…
$y$ （单位： $m$ ）	1	$\frac{9}{8}$	$\frac{5}{4}$	$\frac{11}{8}$	$\frac{3}{2}$	$\frac{13}{8}$	$\frac{7}{4}$	2	…

小区	平均数	中位数	众数
甲	17.2	$m$	18
乙	17.7	19	15