北京市海淀区2022年九年级数学二模试题

试卷更新日期：2022-07-13 类型：中考模拟

进入出卷网下载

一、单选题

1. 如图是某几何体的展开图，该几何体是（）

A、圆柱 B、三棱柱 C、圆锥 D、三棱锥

查看试题解析
2. 为了保护和利用好京杭大运河，我国水利部门启动了京杭大运河2022年全线贯通补水行动，预计总补水量达515000 000 立方米，相当于37个西湖的水量．将515000 000 用科学记数法表示应为（）

A、5.15×10⁸ B、5.15×10⁹ C、0.515×10⁹ D、51.5×10⁷

查看试题解析
3. 五边形的内角和是（）

A、180° B、360° C、540° D、720°

查看试题解析
4. 实数a，b，c 在数轴上的对应点的位置如图所示，则下列结论正确的是（）

A、a＞b B、a + b＞0 C、bc＞0 D、a＜﹣c

查看试题解析
5. 已知m = 2，则代数式2m-1 的值为（）

A、1 B、﹣1 C、3 D、﹣3

查看试题解析
6. “宫商角徵羽”是中国古乐的五个基本音阶（相当于西乐的1，2，3，5，6），是采用“三分损益法”通过数学方法获得．现有一款“一起听古音”的音乐玩具，音乐小球从A处沿轨道进入小洞就可以发出相应的声音，且小球进入每个小洞的可能性大小相同．现有一个音乐小球从A处先后两次进入小洞，先发出“商”音，再发出“羽”音的概率是（）

A、 $\frac{1}{25}$ B、 $\frac{1}{10}$ C、 $\frac{1}{5}$ D、 $\frac{2}{5}$

查看试题解析
7. 如图，为了估算河的宽度，在河对岸选定一个目标点A，在近岸取点B，C，D，E，使得A，B与C共线，A，D与E共线，且直线AC与河岸垂直，直线BD，CE均与直线AC垂直．经测量，得到BC，CE，BD的长度，设AB的长为x，则下列等式成立的是（）

A、 $\frac{x}{x + B C} = \frac{B D}{C E}$ B、 $\frac{x}{B C} = \frac{B D}{C E}$ C、 $\frac{B C}{x + B C} = \frac{B D}{C E}$ D、 $\frac{B C}{x} = \frac{B D}{C E}$

查看试题解析
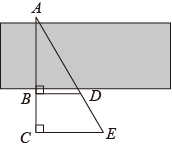8. 从A地到B地有驾车、公交、地铁三种出行方式，为了选择适合的出行方式，对6：00-10：00时段这三种出行方式不同出发时刻所用时长（从A地到B地）进行调查、记录与整理，数据如图所示．
根据统计图提供的信息，下列推断合理的是（）

A、若8：00出发，驾车是最快的出行方式 B、地铁出行所用时长受出发时刻影响较小 C、若选择公交出行且需要30分钟以内到达，则7：30之前出发均可 D、同一时刻出发，不同出行方式所用时长的差最长可达30分钟

查看试题解析

二、填空题

9. 式子 $\sqrt{x - 3}$ 在实数范围内有意义，则 x 的取值范围是．

查看试题解析
10. 方程组 ${\begin{array}{l} x + y = 4 ， \\ 2 x - y = - 1 \end{array}$ 的解为．

查看试题解析
11. 在平面直角坐标系xOy中，点 $A (3 ， y_{1}) ， B (5 ， y_{2})$ 在双曲线 $y = \frac{3}{x}$ 上，则 $y_{1}$ $y_{2}$ （填“＞”或“＜”）．

查看试题解析
12. 用一个a的值说明“若a是实数，则2a一定比a大”是错误的，这个值可以是．

查看试题解析
13. 如图，点A，B，C，D在⊙O上，AC是⊙O的直径．若∠BAC =20°，则∠D的度数为．

查看试题解析
14. 如图，在平行四边形ABCD中，过AC中点O的直线分别交边BC，AD于点E，F，连接AE，CF．只需添加一个条件即可证明四边形AECF 是菱形，这个条件可以是（写出一个即可）．

查看试题解析
15. 如图所示的网格是正方形网格，A，B，C，D是网格线交点．若AB=1，则四边形ABCD的面积为．

查看试题解析
16. 有A，B，C，D，E，F 六种类型的卡牌，每位同学有三张不同类型的卡牌，记作一个“卡牌组合”（不考虑顺序）．将n位同学拥有的卡牌按类型分别统计，得到下表：
卡牌类型
A
B
C
D
E
F
数量（张）
4
10
3
10
1
2
根据以上信息，可知：
①n= ；
②拥有“卡牌组合”的人数最少（横线上填出三张卡牌的类型）．

查看试题解析

三、解答题

17. 计算： $\sqrt{12} - 2 s i n 60 ° + {(\frac{1}{2})}^{- 1} + | - 2 |$

查看试题解析
18. 解不等式组： ${\begin{array}{l} 5 x - 2 > 2 x + 4 ， \\ \frac{x - 1}{2} > \frac{x}{3} ． \end{array}$

查看试题解析
19. 关于x 的方程 $x^{2} - (2 m + 1) x + m^{2} = 0$ 有两个不相等的实数根．

(1)、求m的取值范围；

(2)、当m取最小的整数时，求此时的方程的根．

查看试题解析
20. 如图，在Rt△ABC中，∠A =90°，点D，E，F分别为AB，AC，BC的中点，连接DF，EF．

(1)、求证：四边形AEFD是矩形；

(2)、连接BE，若AB = 2，tan C = $\frac{1}{2}$ ，求BE的长．

查看试题解析
21. 已知：如图1，在△ABC 中，AB = AC，D为边AC上一点．
求作：点P，使得点P 在射线BD上，且∠APB =∠ACB．
作法：如图2，
①以点A为圆心，AB 长为半径画弧，交BD的延长线于点E，
连接AE；
②____．
点P就是所求作的点．

(1)、补全作法，步骤②可为（填“a”或“b”）；
a：作∠BAE的平分线，交射线BD于点P
b：作∠CAE的平分线，交射线BD于点P

(2)、根据（1）中的选择，在图2中使用直尺和圆规，依作法补全图形（保留作图痕迹）；

(3)、由①可知点B， C， E在以点A为圆心，AB长为半径的圆上，所以∠CBE = $\frac{1}{2}$ ∠CAE．
其依据是．
由②可得∠PAD = $\frac{1}{2}$ ∠ ，所以∠PAD =∠CBE．
又因为∠ADP =∠BDC，可证∠APB =∠ACB．

查看试题解析
22. 在平面直角坐标系xOy中，一次函数 $y = k (x - 1) + 6 (k > 0)$ 的图象与反比例函数y= $\frac{m}{x}$ （m≠0）的图象的一个交点的横坐标为1．

(1)、求这个反比例函数的解析式；

(2)、当x＜﹣3时，对于x的每一个值，反比例函数y= $\frac{m}{x}$ 的值大于一次函数 $y = k (x - 1) + 6 (k > 0)$ 的值，直接写出k的取值范围．

查看试题解析
23. 由于惯性的作用，行驶中的汽车在刹车后还要继续向前滑行一段距离才能停止，这段距离称为“刹车距离”．某公司设计了一款新型汽车，现在对它的刹车性能（车速不超过150 km/h）进行测试，测得数据如下表：
车速v（km/h）
0
30
60
90
120
150
刹车距离s（m）
0
7.8
19.2
34.2
52.8
75

(1)、以车速v为横坐标，刹车距离s为纵坐标，在坐标系中描出表中各组数值所对应的点，并用平滑曲线连接这些点；

(2)、由图表中的信息可知：
①该型汽车车速越大，刹车距离越（填“大”或“小”）；
②若该型汽车某次测试的刹车距离为40 m，估计该车的速度约为km/h；

(3)、若该路段实际行车的最高限速为120 km/h，要求该型汽车的安全车距要大于最高限速时刹车距离的3倍，则安全车距应超过m．

查看试题解析
24. 如图，AB为⊙O的直径，CD为弦，CD⊥AB于点E，连接DO并延长交⊙O于点F，连接AF交CD于点G，CG =AG，连接AC．

(1)、求证：AC∥DF；

(2)、若AB = 12，求AC和GD的长．

查看试题解析

25. 某校计划更换校服款式．为调研学生对A，B两款校服的满意度，随机抽取了20名同学试穿两款校服，对舒适性、性价比和时尚性进行评分（满分均为20分），并按照1∶1∶1的比计算综合评分．将数据（评分）进行整理、描述和分析．下面给出了部分信息．

a．A，B两款校服各项评分的平均数（精确到0.1）如下：

款式	舒适性评分平均数	性价比评分平均数	时尚性评分平均数	综合评分平均数
A	19.5	19.6	10.2
B	19.2	18.5	10.4	16.0

b．不同评分对应的满意度如下表：

评分	0≤x＜5	5≤x＜10	10≤x＜15	15≤x≤20
满意度	不满意	基本满意	满意	非常满意

c．A，B两款校服时尚性满意度人数分布统计图如下：

d．B校服时尚性评分在10≤x＜15 这一组的是：

10 11 12 12 14

根据以上信息，回答下列问题：

(1)、在此次调研中，

① A校服综合评分平均数是否达到“非常满意”：（填“是”或“否”）；

② A校服时尚性满意度达到“非常满意”的人数为；

(2)、在此次调研中，B校服时尚性评分的中位数为；

(3)、在此次调研中，记A校服时尚性评分高于其平均数的人数为m，B校服时尚性评分高于其平均数的人数为n．比较m，n的大小，并说明理由．

查看试题解析

26. 在平面直角坐标系xOy中，点（m – 2， y₁），（m， y₂），（2- m， y₃）在抛物线y = x²－2ax + 1上，其中m≠1且m≠2．

(1)、直接写出该抛物线的对称轴的表达式（用含a的式子表示）；

(2)、当m = 0时，若y₁= y₃ ，比较y₁与y₂的大小关系，并说明理由；

(3)、若存在大于1的实数m，使y₁＞y₂＞y₃ ，求a的取值范围．

查看试题解析
27. 已知AB = BC，∠ABC = 90°，直线l是过点B的一条动直线（不与直线AB，BC重合），分别过点A，C作直线l的垂线，垂足为D，E．

(1)、如图1，当45°＜∠ABD＜90°时，
①求证：CE +DE =AD；
②连接AE，过点D作DH⊥AE于H，过点A作AF∥BC交DH的延长线于点F．依题意补全图形，用等式表示线段DF，BE，DE的数量关系，并证明；

(2)、在直线l运动的过程中，若DE的最大值为3，直接写出AB的长．

查看试题解析
28. 在平面直角坐标系xOy中，对于线段MN，直线l和图形W给出如下定义：线段MN关于直线l的对称线段为M'N'（M'，N'分别是M，N的对应点）．若MN与M'N'均在图形W内部（包括边界），则称图形W为线段MN关于直线l的“对称封闭图形”．

(1)、如图，点P（-1，0）．
① 已知图形W₁：半径为1的⊙O，W₂：以线段PO为边的等边三角形，W₃：以O为中心且边长为2的正方形，在W₁ ， W₂ ， W₃中，线段PO关于y轴的“对称封闭图形”是 ▲ ；
② 以O为中心的正方形ABCD的边长为4，各边与坐标轴平行．若正方形ABCD是线段PO关于直线 y = x + b的“对称封闭图形”，求b的取值范围；

(2)、线段MN在由第四象限、原点、x轴正半轴以及y轴负半轴组成的区域内，且MN的长度为2．若存在点Q（ $a - 2 \sqrt{2} ， a + 2 \sqrt{2}$ ），使得对于任意过点Q的直线l，有线段MN，满足半径为r的⊙O是该线段关于l的“对称封闭图形”，直接写出r的取值范围．

查看试题解析

车速v（km/h）	0	30	60	90	120	150
刹车距离s（m）	0	7.8	19.2	34.2	52.8	75

卡牌类型	A	B	C	D	E	F
数量（张）	4	10	3	10	1	2