2022年中考数学真题分类汇编：26 数据分析
试卷更新日期：2022-07-13 类型：二轮复习
一、单选题
-
1. 《义务教育课程标准（2022年版）》首次把学生学会炒菜纳入劳动教育课程，并做出明确规定.某班有7名学生已经学会炒的菜品的种数依次为：3，5，4，6，3，3，4，则这组数据的众数和中位数分别是（ ）A、3，4 B、4，3 C、3，3 D、4，42. 某村通过直播带货对产出的稻虾米进行线上销售，连续7天的销量（单位：袋）分别为：105，103，105，110，108，105，108，这组数据的众数和中位数分别是（ ）A、105，108 B、105，105 C、108，105 D、108，1083. 学校组织学生进行知识竞赛，5名参赛选手的得分分别为：96，97，98，96，98.下列说法中正确的是（ ）A、该组数据的中位数为98 B、该组数据的方差为0.7 C、该组数据的平均数为98 D、该组数据的众数为96和984. 数据1，2，3，4，5，x存在唯一众数，且该组数据的平均数等于众数，则x的值为（ ）A、2 B、3 C、4 D、55. 某校在中国共产主义青年团成立100周年之际，举行了歌咏比赛，七位评委对某个选手的打分分别为：91，88，95，93，97，95，94这组数据的众数和中位数分别是（ ）A、94，94 B、95，95 C、94，95 D、95，946. 五名同学捐款数分别是5，3，6，5，10（单位：元），捐10元的同学后来又追加了10元．追加后的5个数据与之前的5个数据相比，集中趋势相同的是（）A、只有平均数 B、只有中位数 C、只有众数 D、中位数和众数7. 小明同学连续5次测验的成绩分别为：97，97，99，101，106（单位：分），则这组数据的众数和平均数分别为（ ）A、97和99 B、97和100 C、99和100 D、97和1018. 李老师参加本校青年数学教师优质课比赛，笔试得90分、微型课得92分、教学反思得88分.按照图所显示的笔试、微型课、教学反思的权重，李老师的综合成绩为（ ）
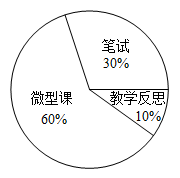A、88 B、90 C、91 D、929. 某路段的一台机动车雷达测速仪记录了一段时间内通过的机动车的车速数据如下：67、63、69、55、65，则该组数据的中位数为（ ）A、63 B、65 C、66 D、6910. A，B两名射击运动员进行了相同次数的射击，下列关于他们射击成绩的平均数和方差的描述中，能说明A成绩较好且更稳定的是（ ）A、 ＞ 且 ＞ ． B、 ＜ 且 ＞ ． C、 ＞ 且 ＜ ． D、 ＜ 且 ＜ ．11. 从 A、B两个品种的西瓜中随机各取7个，它们的质量分布折线图如图．下列统计量中，最能反映出这两组数据之间差异的是（ ）
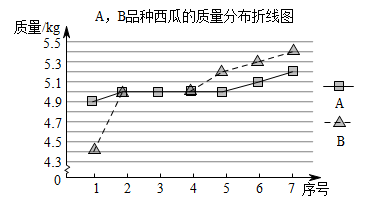A、平均数 B、中位数 C、众数 D、方差12. 今年我国小麦大丰收，农业专家在某种植片区随机抽取了10株小麦，测得其麦穗长（单位：cm）分别为8，8，6，7，9，9，7，8，10，8，那么这一组数据的方差为（ ）A、1.5 B、1.4 C、1.3 D、1.213. 开学前，根据学校防疫要求，小宁同学连续14天进行了体温测量，结果统计如下表：体温(℃)
36.2
36.3
36.5
36.6
36.8
天数(天)
3
3
4
2
2
这14天中，小宁体温的众数和中位数分别为（ ）
A、36.5℃，36.4℃ B、36.5℃，36.5℃ C、36.8C，36.4℃ D、36.8℃，36.5℃14. 在体育测试中，7名女生仰卧起坐的成绩如下（次/分钟）：38，42，42，45，43，45，45，则这组数据的众数是（ ）A、38 B、42 C、43 D、4515. 一组数据4、5、6、a、b的平均数为5，则a、b的平均数为（ ）A、4 B、5 C、8 D、10二、填空题
-
16. 为了落实“双减”，增强学生体质，阳光学校篮球兴趣小组开展投篮比赛活动.6名选手投中篮圈的个数分别为2，3，3，4，3，5，则这组数据的众数是.17. 某中学在一次田径运动会上，参加女子跳高的7名运动员的成绩如下（单位：m）：1.20，1.25，1.10，1.15，1.35，1.30，1.30.这组数据的中位数是.18. 生物学研究表明，植物光合作用速率越高，单位时间内合成的有机物越多，为了解甲、乙两个品种大豆的光合作用速率，科研人员从甲、乙两个品种的大豆中各选五株，在同等实验条件下，测量它们的光合作用速率（单位：），结果统计如下：
品种
第一株
第二株
第三株
第四株
第五株
平均数
甲
32
30
25
18
20
25
乙
28
25
26
24
22
25
则两个大豆品种中光合作用速率更稳定的是（填“甲”或“乙”）．
19. 今年4月23日是第27个世界读书日，某校举行了演讲大赛，演讲得分按“演讲内容”占40%、“语言表达”占40%、“形象风度”占10%、“整体效果”占10%进行计算，小芳这四项的得分依次为85，88，92，90，则她的最后得分是分.20. 学校举行物理科技创新比赛，各项成绩均按百分制计，然后按照理论知识占20%，创新设计占50%，现场展示占30%计算选手的综合成绩（百分制），某同学本次比赛的各项成绩分别是：理论知识85分，创新设计88分，现场展示90分，那么该同学的综合成绩是分.三、综合题
-
21. 综合与实践
【问题情境】数学活动课上，老师带领同学们开展“利用树叶的特征对树木进行分类”的实践活动，
【实践发现】同学们随机收集芒果树、荔枝树的树叶各10片，通过测量得到这些树叶的长y（单位：cm），宽x（单位：cm）的数据后，分别计算长宽比，整理数据如下：
1
2
3
4
5
6
7
8
9
10
芒果树叶的长宽比
3.8
3.7
3.5
3.4
3.8
4.0
3.6
4.0
3.6
4.0
荔枝树叶的长宽比
2.0
2.0
2.0
2.4
1.8
1.9
1.8
2.0
1.3
1.9
【实践探究】分析数据如下：
平均数
中位数
众数
方差
芒果树叶的长宽比
3.74
m
4.0
0.0424
荔枝树叶的长宽比
1.91
1.95
n
0.0669
【问题解决】
(1)、上述表格中， ， ；(2)、①A同学说：“从树叶的长宽比的方差来看，我认为芒果树叶的形状差别大.”②B同学说：“从树叶的长宽比的平均数、中位数和众数来看，我发现荔枝树叶的长约为宽的两倍.”
上面两位同学的说法中，合理的是（填序号）
(3)、现有一片长 ，宽 的树叶，请判断这片树叶更可能来自于芒果、荔枝中的哪种树?并给出你的理由.22. 为振兴乡村经济，在农产品网络销售中实行目标管理，根据目标完成的情况对销售员给予适当的奖励，某村委会统计了15名销售员在某月的销售额（单位：万元），数据如下：10，4，7，5，4，10，5，4，4，18，8，3，5，10，8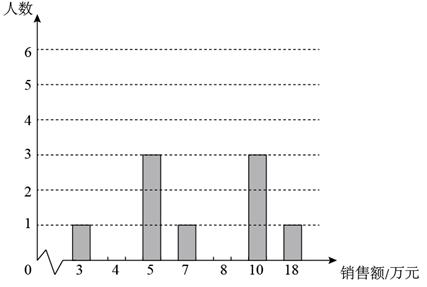
(1)、补全月销售额数据的条形统计图．(2)、月销售额在哪个值的人数最多（众数）？中间的月销售额（中位数）是多少？平均月销售额（平均数）是多少？(3)、根据（2）中的结果，确定一个较高的销售目标给予奖励，你认为月销售额定为多少合适？23. 为落实“双减”政策，优化作业管理，某中学从全体学生中随机抽取部分学生，调查他们每天完成书面作业的时间t（单位：分钟）按照完成时间分成五组：A组“t≤45”，B组“45＜t≤60”，C组“60＜t≤75”，D组“75＜t≤75”，E组“t＞90”将收集的数据整理后，绘制成如下两幅不完整的统计图.根据以上信息，解答下列问题：
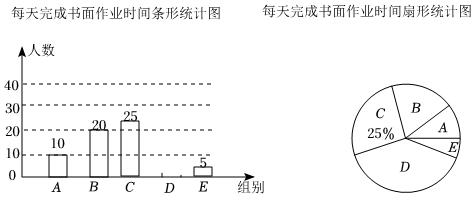(1)、这次调查的样本容量是 ▲ ， 请补全条形统计图；(2)、在扇形统计图中，组的圆心角是度，本次调查数据的中位数落在组内；(3)、若该校有1800名学生，请你估计该校每天完成书面作业不超过90分钟的学生人数.24. 某公司要在甲、乙两人中招聘一名职员，对两人的学历、能力、经验这三项进行了测试，各项满分均为10分，成绩高者被录用．图1是甲、乙测试成绩的条形统计图．
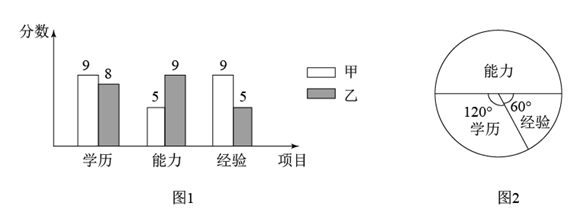(1)、分别求出甲、乙三项成绩之和，并指出会录用谁；(2)、若将甲、乙的三项测试成绩，按照扇形统计图（图2）各项所占之比，分别计算两人各自的综合成绩，并判断是否会改变（1）的录用结果．25. 某校九年级640名学生在“信息素养提升”培训前、后各参加了一次水平相同的测试，并以同一标准折算成“6分”、“7分”、“8分”、“9分”、“10分”5个成绩.为了解培训效果，用抽样调查的方式从中抽取了32名学生的2次测试成绩，并用划记法制成了如下表格：培训前
成绩（分）
6
7
8
9
10
划记
正正
正
正
人数（人）
12
4
7
5
4
培训后
成绩（分）
6
7
8
9
10
划记
一
正
正正正
人数（人）
4
1
3
9
15
(1)、这32名学生2次测试成绩中，培训前测试成绩的中位数是m，培训后测试成绩的中位数是n，则mn；（填“＞”、“＜”或“＝”）(2)、这32名学生经过培训，测试成绩为“6分”的百分比比培训前减少了多少？(3)、估计该校九年级640名学生经过培训，测试成绩为“10分”的学生增加了多少人？26. 为落实“双减”政策，优化作业管理，某中学从全体学生中随机抽取部分学生，调查他们每天完成书面作业的时间t（单位：分钟）.按照完成时间分成五组：A组“t≤45”，B组“45＜t≤60”，C组“60＜t≤75”，D组“75＜t≤90”，E组“t＞90”.将收集的数据整理后，绘制成如下两幅不完整的统计图. 根据以上信息，解答下列问题：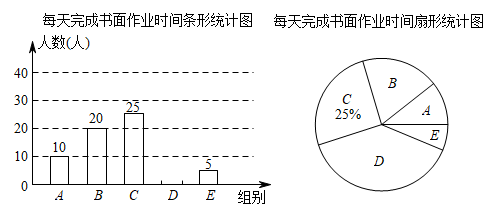
(1)、这次调查的样本容量是 ▲ ， 请补全条形统计图；(2)、在扇形统计图中，B组的圆心角是度，本次调查数据的中位数落在组内；(3)、若该校有1800名学生，请你估计该校每天完成书面作业不超过90分钟的学生人数.