(沪教版)2022年暑假六年级数学复习巩固专题15 角的大小的比较、画相等的角
试卷更新日期:2022-07-13 类型:复习试卷
一、单选题
-
1. 已知 , , 则∠BOC的度数为( )A、78° B、42° C、78°或42° D、102°或48°2. 如图,OA⊥OB,OC⊥OD,O是垂足,∠AOD=120°,那么∠COB的度数为( )
 A、80° B、70° C、60° D、50°3. 如图, 于O,直线CD经过O, ,则 的度数是( )
A、80° B、70° C、60° D、50°3. 如图, 于O,直线CD经过O, ,则 的度数是( ) A、 B、 C、 D、4. 如图,一副三角板(直角顶点重合)摆放在桌面上,若 ,则 等于( )
A、 B、 C、 D、4. 如图,一副三角板(直角顶点重合)摆放在桌面上,若 ,则 等于( )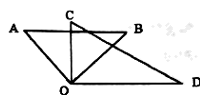 A、 B、 C、 D、5. 关于角的描述不正确的是( )
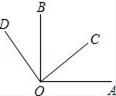
A、 B、 C、 D、5. 关于角的描述不正确的是( ) A、∠1与∠AOB表示同一个角 B、∠AOC可以用∠O表示 C、∠AOC=∠AOB+∠BOC D、∠β表示∠BOC6. 如图,BD在∠ABC的内部,∠ABD=∠CBD,如果∠ABC=80°,则∠ABD=( )
A、∠1与∠AOB表示同一个角 B、∠AOC可以用∠O表示 C、∠AOC=∠AOB+∠BOC D、∠β表示∠BOC6. 如图,BD在∠ABC的内部,∠ABD=∠CBD,如果∠ABC=80°,则∠ABD=( ) A、 B、20° C、60° D、7. 如图, , 直线EF经过点C,若 , 则的大小为( )
A、 B、20° C、60° D、7. 如图, , 直线EF经过点C,若 , 则的大小为( ) A、56° B、66° C、54° D、46°8. 如图∠AOC+∠COD-∠AOB=( )
A、56° B、66° C、54° D、46°8. 如图∠AOC+∠COD-∠AOB=( ) A、∠AOC B、∠BOC C、∠BOD D、∠AOD9. 只借助一副三角尺拼摆,不能画出下列哪个度数的角( )A、15° B、65° C、75° D、135°10. 图中哪一个角的度数最接近45°( )
A、∠AOC B、∠BOC C、∠BOD D、∠AOD9. 只借助一副三角尺拼摆,不能画出下列哪个度数的角( )A、15° B、65° C、75° D、135°10. 图中哪一个角的度数最接近45°( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,已知AB,CD相交于点O,于O, , 则的度数是 .
 12. 如图,直线AB、CD相交于点O,OE⊥AB于点O,且∠COE=34°,则∠AOD为 .
12. 如图,直线AB、CD相交于点O,OE⊥AB于点O,且∠COE=34°,则∠AOD为 . 13. 如图,将一个三角板60°角的顶点与另一个三角板的直角顶点重合,∠1=27°,∠2= .
13. 如图,将一个三角板60°角的顶点与另一个三角板的直角顶点重合,∠1=27°,∠2= .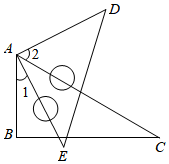 14. 计算:50°﹣45°30'=.15. 如图, 的度数是 .
14. 计算:50°﹣45°30'=.15. 如图, 的度数是 .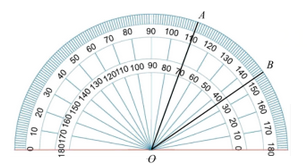
三、解答题
-
16. 如图,点O为直线AB上的一点,已知∠1=65°15′,∠2=78°30′,求∠1+∠2﹣∠3的大小.
 17. 如图,已知∠AOC=90°,∠BOD=90°,∠BOC=38°19′,求∠AOD的度数.
17. 如图,已知∠AOC=90°,∠BOD=90°,∠BOC=38°19′,求∠AOD的度数. 18. 如图,O是直线上一点, , 求的度数.
18. 如图,O是直线上一点, , 求的度数. 19. 如图,直线 与直线 相交于点 , ,垂足为 , ,求 的度数.
19. 如图,直线 与直线 相交于点 , ,垂足为 , ,求 的度数. 20. 如图,直线 , 垂足为 , 直线 经过点 , , 求 , , 的度数.
20. 如图,直线 , 垂足为 , 直线 经过点 , , 求 , , 的度数. 21. 如图,已知, 是直线 上一点, ,射线 平分 , .求 的度数.
21. 如图,已知, 是直线 上一点, ,射线 平分 , .求 的度数. 22. 下面是小马虎解的一道题
22. 下面是小马虎解的一道题题目:在同一平面上,若∠BOA=70°,∠BOC=15°求∠AOC的度数.
解:根据题意可画出图,
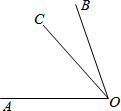
∵∠AOC=∠BOA-∠BOC
=70°-15°
=55°,
∴∠AOC=55°.
若你是老师,会判小马虎满分吗?若会,说明理由.若不会,请将小马虎的的错误指出,并给出你认为正确的解法.

