2022-2023学年苏科版数学九年级上学期1.4.3 一元二次方程应用——几何问题 同步训练
试卷更新日期：2022-07-13 类型：同步测试
一、单选题
-
1. 如图所示，A，B，C，D为矩形的四个顶点，AB=16cm，AD=8cm，动点P，Q分别从点A，C同时出发，点P以3cm/s的速度向B移动，一直到达B为止；点Q以2cm/s的速度向D移动．当P，Q两点从出发开始几秒时，点P和点Q的距离是10cm．(若一点到达终点，另一点也随之停止运动)（ ）
A、2s或s B、1s或s C、s D、2s或s2. 如图， 中， ， cm， cm，动点 从点 出发沿 边以 cm /秒的速度向点 移动，点 从点 出发，沿 边以 cm /秒的速度向点 移动，如果点 ， 分别从点 ， 同时出发，在运动过程中，设点 的运动时间为 ，则当 的面积为 cm2时， 的值（ ）
A、2或3 B、2或4 C、1或3 D、1或43. 把一块长与宽之比为2：1的铁皮的四角各剪去一个边长为10厘米的小正方形，折起四边，可以做成一个无盖的盒子，如果这个盒子的容积是1500立方厘米，设铁皮的宽为x厘米，则正确的方程是（ ）A、（2x﹣20）（x﹣20）=1500 B、10（2x﹣10）（x﹣10）=1500 C、10（2x﹣20）（x﹣20）=1500 D、10（x﹣10）（x﹣20）=15004. 如图，将边长 的正方形 沿其对角线 剪开，再把 沿着 方向平移，得到 ，若两个三角形重叠部分的面积为 ，则它移动的距离 等于（ ）
A、 B、 C、 D、5. 如图，AB⊥BC，AB＝10 cm，BC＝8 cm，一只蝉从C点沿CB方向以每秒1 cm的速度爬行，蝉开始爬行的同时，一只螳螂由A点沿AB方向以每秒2 cm的速度爬行，当螳螂和蝉爬行x秒后，它们分别到达了M，N的位置，此时，△MNB的面积恰好为24 cm，由题意可列方程（ ）
A、2x·x＝24 B、(10－2x)(8－x)＝24 C、(10－x)(8－2x)＝24 D、(10－2x)(8－x)＝48二、填空题
-
6. 在设计人体雕像时，使雕像的上部（腰以上）与下部（腰以下）的高度比，等于下部与全部（全身）的高度比，可以增加视觉美感．按此比例，如果雕像的高为 ，设雕像下部高为 ，则可得到方程 ．7. 《九章算术》是我国古代的数学名著，其中“勾股”章有一题，大意是说：已知矩形门的高比宽多 尺，门的对角线长 尺，那么门的高和宽各是多少?如果设门的宽为 尺，根据题意，那么可列方程 ．8. 我国古代数学名著《算法统宗）有一道“荡秋干”的问题，“平地秋千未起，踏板一尺离地.送行二步与人齐，5尺人高曾记，仕女家人争蹴.良工高士素好奇，算出索长有几？”此问题可理解为：如图，有一架秋千，当它静止时，踏板离地距离PA的长为1尺，将它向前水平推送10尺时，即 尺，秋千踏板离地的距离 就和身高5尺的人一样高，秋千的绳索始终拉得很直，则秋千的绳索长为尺.
9. 如图，在△ABC中，∠C=90°，BC=8cm，AC=6cm，点E是BC的中点，动点P从A点出发以每秒2cm的速度沿A→C→B运动，设点P运动的时间是t秒，那么当t= ， △APE的面积等于6.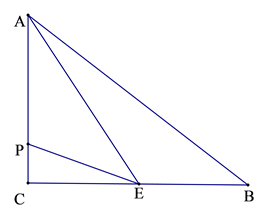
10. 在 中， ， ， ，动点 从 开始向 以 速度移动，点 从 开始向 以 的速度移动，点 到 后停止，点 到 后停止，则能使 面积为 的时间为 ．
三、解答题
-
11. 如图，把一块长为20cm，宽为15cm的矩形硬纸板的四角剪去四个相同小正方形，然后把纸板的四边沿虚线折起，并用胶带粘好，即可做成一个无盖纸盒．若该无盖纸盒的底面积为150cm2 ， 求剪去小正方形的边长．
12. 如图，在矩形ABCD中，AB＝6cm，BC＝3cm，点P沿边AB从点A开始向点B以2cm/s的速度运动，点Q沿边DA从点D开始向点A以1cm/s的速度运动.如果P、Q同时出发，运动时间为t（s）（0≤t≤3）.
(1)、AP＝cm，AQ＝cm；(2)、t为何值时，△QAP的面积等于2cm2？13. 已知矩形的一边长为2，另一边长为1.(1)、是否存在另一个矩形，它的周长和面积分别是已知矩形周长和面积的2倍？小明是这样想的：小刚是这样想的：
按照小明思路，完成解答：
根据小刚的思路，直接写出两个交点坐标；
(2)、如果存在另一个矩形，周长是已知矩形周长的2倍，面积是已知矩形面积的 倍 ，求 的取值范围.14. 如图是一个五边形的空地ABCDE，∠B＝∠C＝∠D＝90°，∠A＝135°，已知AB＝4m，BC＝8m，CD＝10m，DE＝2m，准备在五边形ABCDE内按如图方式设计一个长方形FGCH铺设木地板，剩下部分铺设地砖.点F，G，H分别在边AE，BC，CD上.
(1)、求五边形ABCDE的面积；(2)、若长方形FGCH的面积为35m2 ， 求BG的长.(3)、若铺设木地板的成本为每平方米200元，铺设地砖的成本为每平方米100元，投资7300元能否完成地面铺设？通过计算说明.15. 某单位要兴建一个长方形的活动区（图中阴影部分），根据规划活动区的长和宽分别为21m和12m，同时要在它四周外围修建宽度相等的小路．已知活动区和小路的总面积为400m2 ．
(1)、求小路的宽度；(2)、某公司希望用50万元承包这项工程，该单位认为金额太高需要降价，通过两次协商，最终以40.5万元达成一致．若两次降价的百分率相同，求每次降价的百分率．16. 某社区利用一块长方形空地建了一个小型的惠民停车场，其布局如图所示.已知停车场的长为52米，宽为28米，阴影部分设计为停车位，要铺花砖，其余部分是等宽的通道.已知铺花砖的面积为640平方米.
(1)、求通道的宽是多少米.(2)、该停车场共有车位64个，据调查分析，当每个车位的月租金为200元时，可全部租出；当每个车位的月租金每上涨10元，就会少租出1个车位，当每个车位的月租金上涨多少元时，停车场的月租金收入为14400元且使租出的车位较多？17. 如图，用一段77米的篱笆围成三个一边靠墙、大小相同的矩形羊圈，每个矩形都有一个1米的门，墙的最大可用长度为30米．
(1)、如果羊圈的总面积为300平方米，求边 的长；(2)、羊圈的总面积能为500平方米吗？若能，请求出边 的长；若不能，说明理由．