解三角形（解答题）——大数据之五年（2018-2022）高考真题汇编（新高考卷与全国理科）

试卷更新日期：2022-07-13 类型：二轮复习

进入出卷网下载

一、解答题

1. 在 $△ A B C$ 中，角A，B，C所对的边分别为a，b，c．
已知 $4 a = \sqrt{5} c ， \cos C = \frac{3}{5}$ ．

（Ⅰ）求 $\sin A$ 的值；

（Ⅱ）若 $b = 11$ ，求 $△ A B C$ 的面积．

查看试题解析
2. 记 $△ A B C$ 的三个内角分别为A，B，C，其对边分别为a，b，c，分别以a，b，c为边长的三个正三角形的面积依次为 $S_{1} ， S_{2} ， S_{3}$ ，已知 $S_{1} - S_{2} + S_{3} = \frac{\sqrt{3}}{2} ， \sin B = \frac{1}{3}$ ．

(1)、求 $△ A B C$ 的面积；

(2)、若 $\sin A \sin C = \frac{\sqrt{2}}{3}$ ，求b．

查看试题解析
3. 记 $△ A B C$ 的内角A，B，C的对边分别为a，b，c﹐已知 $\sin C \sin (A - B) = \sin B \sin (C - A)$ ．

(1)、若 $A = 2 B$ ，求C；

(2)、证明： $2 a^{2} = b^{2} + c^{2}$ .

查看试题解析
4. 记 $△ A B C$ 的内角 $A ， B ， C$ 的对边分别为 $a ， b ， c$ ，已知 $\sin C \sin (A - B) = \sin B \sin (C - A)$ ．

(1)、证明： $2 a^{2} = b^{2} + c^{2}$ ；

(2)、若 $a = 5 ， \cos A = \frac{25}{31}$ ，求 $△ A B C$ 的周长．

查看试题解析
5. 在 $△ A B C$ 中， $\sin 2 C = \sqrt{3} \sin C$ ．
（I）求 $∠ C$ ：

（II）若 $b = 6$ ，且 $△ A B C$ 的面积为 $6 \sqrt{3}$ ，求 $△ A B C$ 的周长．

查看试题解析
6. 记 $△ A B C$ 的内角A，B，C的对边分别为a，b，c，已知 $\frac{cos A}{1 + sin A} = \frac{sin 2 B}{1 + cos 2 B} .$

(1)、若 $C = \frac{2 π}{3} ，$ 求B；

(2)、求 $\frac{a^{2} + b^{2}}{c^{2}}$ 的最小值.

查看试题解析
7. 已知点A(2，1)在双曲线 C： $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{a^{2} - 1} = 1 (a > 1)$ 上，直线 $l$ 交C于P，Q两点，直线
AP，AQ的斜率之和为0.

(1)、求 $l$ 的斜率；

(2)、若 $tan ∠ P A Q = 2 \sqrt{2} ，$ 求 $P A Q$ 的面积.

查看试题解析
8. 在 $△ A B C$ 中，角A，B，C所对的边长分别为 $a ， b ， c ， b = a + 1 ， c = a + 2$ ．

(1)、若 $2 \sin C = 3 \sin A$ ，求 $△ A B C$ 的面积；

(2)、是否存在正整数a，使得 $△ A B C$ 为钝角三角形?若存在，求出a的值；若不存在，说明理由．

查看试题解析
9. 已知在 $△ A B C$ 中， $c = 2 b \cos B$ ， $C = \frac{2 π}{3}$ ．

(1)、求 $B$ 的大小；

(2)、在下列三个条件中选择一个作为已知，使 $△ A B C$ 存在且唯一确定，并求出 $B C$ 边上的中线的长度．
① $c = \sqrt{2} b$ ；②周长为 $4 + 2 \sqrt{3}$ ；③面积为 $S_{Δ A B C} = \frac{3 \sqrt{3}}{4}$ ；

查看试题解析
10. 在 $△ A B C$ ，角 $A ， B ， C$ 所对的边分别为 $a ， b ， c$ ，已知 $\sin A ： \sin B ： \sin C = 2 ： 1 ： \sqrt{2}$ ， $b = \sqrt{2}$ ．

(1)、求a的值；

(2)、求 $\cos C$ 的值；

(3)、求 $\sin (2 C - \frac{π}{6})$ 的值．

查看试题解析
11. 记△ABC的内角A，B，C的对边分别为a.，b.，c，已知 $b^{2}$ =ac，点D在边AC 上，BDsin∠ABC=asinC.

(1)、证明：BD = b：

(2)、若AD = 2DC .求cos∠ABC.

查看试题解析
12. $△ A B C$ 中，sin²A－sin²B－sin²C=sinBsinC．

(1)、求A；

(2)、若BC=3，求 $△ A B C$ 周长的最大值.

查看试题解析
13. 在① $a c = \sqrt{3}$ ，② $c sin A = 3$ ，③ $c = \sqrt{3} b$ 这三个条件中任选一个，补充在下面问题中，若问题中的三角形存在，求 $c$ 的值；若问题中的三角形不存在，说明理由．
问题：是否存在 $△ A B C$ ，它的内角 $A, B, C$ 的对边分别为 $a, b, c$ ，且 $sin A = \sqrt{3} sin B$ ， $C = \frac{π}{6}$ ， ▲ ?

注：如果选择多个条件分别解答，按第一个解答计分．

查看试题解析
14. 在 $△ A B C$ 中，角 $A, B, C$ 所对的边分别为 $a, b, c$ ．已知 $a = 2 \sqrt{2}, b = 5, c = \sqrt{13}$ ．
（Ⅰ）求角C的大小；

（Ⅱ）求 $\sin A$ 的值；

（Ⅲ）求 $\sin (2 A + \frac{π}{4})$ 的值．

查看试题解析
15. 在△ABC中，角A，B，C的对边分别为a，b，c，已知 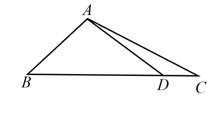$a = 3 ， c = \sqrt{2} ， B = 45 °$ ．

(1)、求 $\sin C$ 的值；

(2)、在边BC上取一点D，使得 $\cos ∠ A D C = - \frac{4}{5}$ ，求 $\tan ∠ D A C$ 的值．

查看试题解析
16. 在 $△ A B C$ 中， $a + b = 11$ ，再从条件①、条件②这两个条件中选择一个作为已知，求：
（Ⅰ）a的值：

（Ⅱ） $\sin C$ 和 $△ A B C$ 的面积．

条件①： $c = 7 ， \cos A = - \frac{1}{7}$ ；

条件②： $\cos A = \frac{1}{8} ， \cos B = \frac{9}{16}$ ．

注：如果选择条件①和条件②分别解答，按第一个解答计分．

查看试题解析
17. 在锐角△ABC中，角A，B，C的对边分别为a，b，c，且2bsinA＝ $\sqrt{3}$ a．
（Ⅰ）求角B；

（Ⅱ）求cosA+cosB+cosC的取值范围．

查看试题解析
18. 在△ABC中，角A ， B ， C的对边分别为a ， b ， c ．

(1)、若a=3c ， b= $\sqrt{2}$ ，cosB= $\frac{2}{3}$ ，求c的值；

(2)、若 $\frac{\sin A}{a} = \frac{\cos B}{2 b}$ ，求 $\sin (B + \frac{π}{2})$ 的值．

查看试题解析
19. 在 $△ A B C$ 中，内角 $A, B, C$ 所对的边分别为 $a, b, c$ .已知 $b + c = 2 a$ ， $3 c \sin B = 4 a \sin C$ .
（Ⅰ）求 $\cos B$ 的值；

（Ⅱ）求 $\sin (2 B + \frac{π}{6})$ 的值.

查看试题解析
20. △ABC的内角A、B、C的对边分别为a，b，c，已知 $a \sin \frac{A + C}{2} = b \sin A$

(1)、求B；

(2)、若△ABC为锐角三角形，且c=1，求△ABC面积的取值范围.

查看试题解析
21. 在△ABC中，a=3，b-c=2，cosB=- $\frac{1}{2}$ .
（I）求b，c的值：

（II）求sin（B+C）的值.

查看试题解析
22. 在△ABC中，a=3，b-c=2，cosB=- $\frac{1}{2}$ .
（I）求b，c的值；
（II）求sin（B-C）的值.

查看试题解析
23. ∆ABC的内角A，B，C的对边分别为a，b，c.设(sinB-sinC)²=sin²A-sinBsinC。

(1)、求A；

(2)、若 $\sqrt{2} a + b = 2 c$ ,求sinC.

查看试题解析
24. 在平面四边形 $A B C D$ 中， $∠ A D C = 90^{\circ} ，$ $∠ A = 45^{\circ} ，$ $A B = 2 ，$ $B D = 5.$

(1)、求 $\cos ∠ A D B$ ；

(2)、若 $D C = 2 \sqrt{2} ，$ 求 $B C$ .

查看试题解析
25. 在 $Δ A B C$ 中，内角A ， B，C所对的边分别为a，b ， c. 已知 $b \sin A = a \cos (B - \frac{π}{6})$ .
（Ⅰ）求角B的大小；
（Ⅱ）设a=2，c=3，求b和 $\sin (2 A - B)$ 的值.

查看试题解析
26. 在△ABC中，a=7，b=8，cosB=- $\frac{1}{7}$ ，
（Ⅰ）求∠A：
（Ⅱ）求AC边上的高。

查看试题解析