立体几何(解答题)——大数据之五年(2018-2022)高考真题汇编(新高考卷与全国理科)
试卷更新日期:2022-07-13 类型:二轮复习
一、解答题
-
1. 如图, 是三棱锥 的高, , ,E是 的中点.
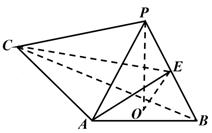 (1)、求证: 平面 ;(2)、若 , , ,求二面角 的正弦值.2. 如图,四面体 中, ,E为AC的中点.
(1)、求证: 平面 ;(2)、若 , , ,求二面角 的正弦值.2. 如图,四面体 中, ,E为AC的中点.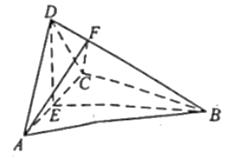 (1)、证明:平面 平面ACD;(2)、设 ,点F在BD上,当 的面积最小时,求三棱锥 的体积.3. 在四棱锥 中, 底面 .
(1)、证明:平面 平面ACD;(2)、设 ,点F在BD上,当 的面积最小时,求三棱锥 的体积.3. 在四棱锥 中, 底面 .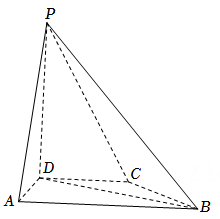 (1)、证明: ;(2)、求PD与平面 所成的角的正弦值.4. 小明同学参加综合实践活动,设计了一个封闭的包装盒,包装盒如图所示:底面 是边长为8(单位:cm)的正方形, 均为正三角形,且它们所在的平面都与平面 垂直.
(1)、证明: ;(2)、求PD与平面 所成的角的正弦值.4. 小明同学参加综合实践活动,设计了一个封闭的包装盒,包装盒如图所示:底面 是边长为8(单位:cm)的正方形, 均为正三角形,且它们所在的平面都与平面 垂直.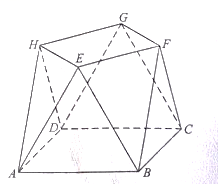 (1)、证明: 平面 ;(2)、求该包装盒的容积(不计包装盒材料的厚度).5. 如图,四面体 中, ,E为 的中点.
(1)、证明: 平面 ;(2)、求该包装盒的容积(不计包装盒材料的厚度).5. 如图,四面体 中, ,E为 的中点. (1)、证明:平面 平面 ;(2)、设 ,点F在 上,当 的面积最小时,求 与平面 所成的角的正弦值.6. 如图,在三棱柱 中,侧面 为正方形,平面 平面 , , 分别为 , 的中点.
(1)、证明:平面 平面 ;(2)、设 ,点F在 上,当 的面积最小时,求 与平面 所成的角的正弦值.6. 如图,在三棱柱 中,侧面 为正方形,平面 平面 , , 分别为 , 的中点.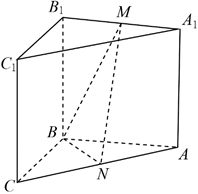
(I)求证: 平面 ;
(II)再从条件①、条件②这两个条件中选择一个作为已知,求
直线 与平面 所成角的正弦值。
条件①: ;
条件②: .
注:如果选择条件①和条件②分别解答,按第一个解答计分。
7. 如图,直三棱柱 的体积为4, '的面积为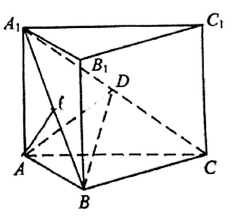 (1)、求A到平面 的距离;(2)、设D为 的中点, 平面 平面 求二面角 的正弦值.8. 在四棱锥 中,底面 是正方形,若 .
(1)、求A到平面 的距离;(2)、设D为 的中点, 平面 平面 求二面角 的正弦值.8. 在四棱锥 中,底面 是正方形,若 . (1)、证明:平面 平面 ;(2)、求二面角 的平面角的余弦值.9. 已知正方体 ,点 为 中点,直线 交平面 于点 .
(1)、证明:平面 平面 ;(2)、求二面角 的平面角的余弦值.9. 已知正方体 ,点 为 中点,直线 交平面 于点 .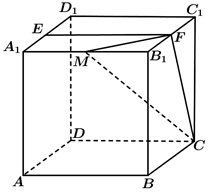 (1)、证明:点 为 的中点;(2)、若点 为棱 上一点,且二面角 的余弦值为 ,求 的值.10. 如图,在四棱锥 中,底面 是平行四边形, ,M , N分别为 的中点, .
(1)、证明:点 为 的中点;(2)、若点 为棱 上一点,且二面角 的余弦值为 ,求 的值.10. 如图,在四棱锥 中,底面 是平行四边形, ,M , N分别为 的中点, .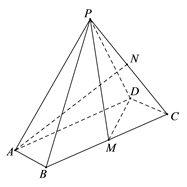 (1)、证明: ;(2)、求直线 与平面 所成角的正弦值.11. 如图,四棱锥P-ABCD的底面是矩形,PD 底面ABCD,M为BC的中点,且PB AM.
(1)、证明: ;(2)、求直线 与平面 所成角的正弦值.11. 如图,四棱锥P-ABCD的底面是矩形,PD 底面ABCD,M为BC的中点,且PB AM.
 (1)、证明:平面PAM 平面PBD;(2)、若PD=DC=1,求四棱锥P-ADCD的体积.12. 已知直三棱柱 中,侧面 为正方形. 分别为 和 的中点, .
(1)、证明:平面PAM 平面PBD;(2)、若PD=DC=1,求四棱锥P-ADCD的体积.12. 已知直三棱柱 中,侧面 为正方形. 分别为 和 的中点, .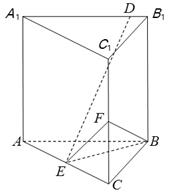 (1)、求三棱锥F-EBC的体积;(2)、已知 为棱 上的点,证明: .13. 已知直三棱柱ABC-A1B1C1.中,侧面AA1B1B为正方形,AB= BC = 2,E,F分别为AC和CC1的中点,D为棱A1B1上的点,BF丄A1B1.
(1)、求三棱锥F-EBC的体积;(2)、已知 为棱 上的点,证明: .13. 已知直三棱柱ABC-A1B1C1.中,侧面AA1B1B为正方形,AB= BC = 2,E,F分别为AC和CC1的中点,D为棱A1B1上的点,BF丄A1B1.
 (1)、 证明:BF⊥DE;(2)、当为B1D何值时,面BB1C1C与面DFE所成的二面角的正弦值最小?14. 如图,四棱锥P-ABCD的底面是矩形,PD⊥底面ABCD,PD=DC=1,M为BC的中点,且PB⊥AM,
(1)、 证明:BF⊥DE;(2)、当为B1D何值时,面BB1C1C与面DFE所成的二面角的正弦值最小?14. 如图,四棱锥P-ABCD的底面是矩形,PD⊥底面ABCD,PD=DC=1,M为BC的中点,且PB⊥AM, (1)、求BC;(2)、求二面角A-PM-B的正弦值。15. 如图,在棱长为2的正方体 中,E为棱BC的中点,F为棱CD的中点.
(1)、求BC;(2)、求二面角A-PM-B的正弦值。15. 如图,在棱长为2的正方体 中,E为棱BC的中点,F为棱CD的中点.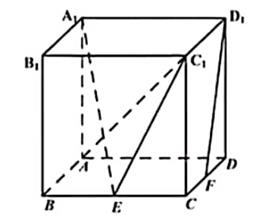 (1)、求证: 平面 ;(2)、求直线 与平面 所成角的正正弦值.(3)、求二面角 的正弦值.16. 如图,在三棱锥A-BCD中.平面ABD丄平面BCD,AB=AD.O为BD的中点.
(1)、求证: 平面 ;(2)、求直线 与平面 所成角的正正弦值.(3)、求二面角 的正弦值.16. 如图,在三棱锥A-BCD中.平面ABD丄平面BCD,AB=AD.O为BD的中点.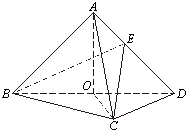 (1)、证明:OA⊥CD:(2)、若△OCD是边长为1的等边三角形.点E在 棱AD上.DE=2EA.且二面角E-BC-D的大小为45°,求三棱锥A-BCD的体积.17. 如图,在长方体 中,点 分别在棱 上,且 , .
(1)、证明:OA⊥CD:(2)、若△OCD是边长为1的等边三角形.点E在 棱AD上.DE=2EA.且二面角E-BC-D的大小为45°,求三棱锥A-BCD的体积.17. 如图,在长方体 中,点 分别在棱 上,且 , . (1)、证明:点 在平面 内;(2)、若 , , ,求二面角 的正弦值.18. 如图,已知三棱柱ABC-A1B1C1的底面是正三角形,侧面BB1C1C是矩形,M,N分别为BC,B1C1的中点,P为AM上一点,过B1C1和P的平面交AB于E,交AC于F.
(1)、证明:点 在平面 内;(2)、若 , , ,求二面角 的正弦值.18. 如图,已知三棱柱ABC-A1B1C1的底面是正三角形,侧面BB1C1C是矩形,M,N分别为BC,B1C1的中点,P为AM上一点,过B1C1和P的平面交AB于E,交AC于F.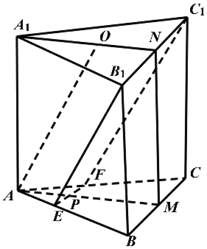 (1)、证明:AA1∥MN,且平面A1AMN⊥EB1C1F;(2)、设O为△A1B1C1的中心,若AO∥平面EB1C1F,且AO=AB,求直线B1E与平面A1AMN所成角的正弦值.19. 如图,D为圆锥的顶点,O是圆锥底面的圆心, 为底面直径, . 是底面的内接正三角形,P为 上一点, .
(1)、证明:AA1∥MN,且平面A1AMN⊥EB1C1F;(2)、设O为△A1B1C1的中心,若AO∥平面EB1C1F,且AO=AB,求直线B1E与平面A1AMN所成角的正弦值.19. 如图,D为圆锥的顶点,O是圆锥底面的圆心, 为底面直径, . 是底面的内接正三角形,P为 上一点, . (1)、证明: 平面 ;(2)、求二面角 的余弦值.20. 如图,四棱锥P-ABCD的底面为正方形,PD⊥底面ABCD.设平面PAD与平面PBC的交线为l.
(1)、证明: 平面 ;(2)、求二面角 的余弦值.20. 如图,四棱锥P-ABCD的底面为正方形,PD⊥底面ABCD.设平面PAD与平面PBC的交线为l.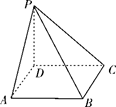 (1)、证明:l⊥平面PDC;(2)、已知PD=AD=1,Q为l上的点,求PB与平面QCD所成角的正弦值的最大值.21. 如图,在三棱柱 中, 平面 , ,点 分别在棱 和棱 上,且 为棱 的中点.
(1)、证明:l⊥平面PDC;(2)、已知PD=AD=1,Q为l上的点,求PB与平面QCD所成角的正弦值的最大值.21. 如图,在三棱柱 中, 平面 , ,点 分别在棱 和棱 上,且 为棱 的中点.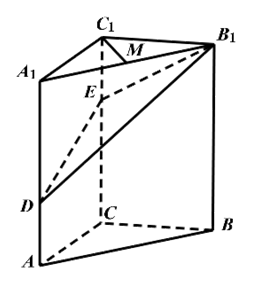
(Ⅰ)求证: ;(Ⅱ)求二面角 的正弦值;
(Ⅲ)求直线 与平面 所成角的正弦值.
22. 在三棱锥A—BCD中,已知CB=CD= ,BD=2,O为BD的中点,AO⊥平面BCD,AO=2,E为AC的中点.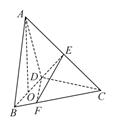 (1)、求直线AB与DE所成角的余弦值;(2)、若点F在BC上,满足BF= BC,设二面角F—DE—C的大小为θ,求sinθ的值.23. 在三棱柱ABC-A1B1C1中,AB⊥AC,B1C⊥平面ABC,E,F分别是AC,B1C的中点.
(1)、求直线AB与DE所成角的余弦值;(2)、若点F在BC上,满足BF= BC,设二面角F—DE—C的大小为θ,求sinθ的值.23. 在三棱柱ABC-A1B1C1中,AB⊥AC,B1C⊥平面ABC,E,F分别是AC,B1C的中点.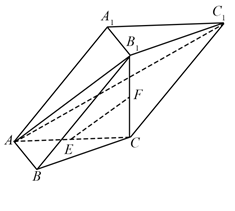 (1)、求证:EF∥平面AB1C1;(2)、求证:平面AB1C⊥平面ABB1 .24. 如图,在正方体 中,E为 的中点.
(1)、求证:EF∥平面AB1C1;(2)、求证:平面AB1C⊥平面ABB1 .24. 如图,在正方体 中,E为 的中点.
(Ⅰ)求证: 平面 ;(Ⅱ)求直线 与平面 所成角的正弦值.
25. 如图,在直三棱柱ABC-A1B1C1中,D , E分别为BC , AC的中点,AB=BC .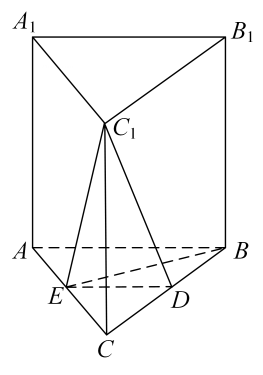
求证:
(1)、A1B1∥平面DEC1;(2)、BE⊥C1E .26. 如图,已知三棱柱ABC-A1B1C1 , 平面A1AC1C⊥平面ABC,∠ABC=90°.∠BAC=30°,A1A=A1C=AC,E,F分别是AC,A1B1的中点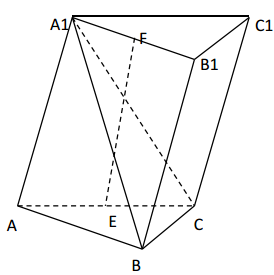 (1)、证明:EF⊥BC(2)、求直线EF与平面A1BC所成角的余弦值.27. 如图,在四棱锥 中,底面 为平行四边形, 为等边三角形,平面 平面 , , ,
(1)、证明:EF⊥BC(2)、求直线EF与平面A1BC所成角的余弦值.27. 如图,在四棱锥 中,底面 为平行四边形, 为等边三角形,平面 平面 , , ,
(Ⅰ)设 分别为 的中点,求证: 平面 ;
(Ⅱ)求证: 平面 ;
(Ⅲ)求直线 与平面 所成角的正弦值.
28. 如图, 平面 , , .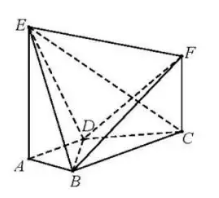
(Ⅰ)求证: 平面 ;
(Ⅱ)求直线 与平面 所成角的正弦值;
(Ⅲ)若二面角 的余弦值为 ,求线段 的长.
29. 图1是由矩形ADEB、Rt△ABC和菱形BFCC组成的一个平面图形,其中AB=1,BE=BF=2,∠FBC=60°,将其沿AB,BC折起使得BE与BF重合,连结DC,如题2.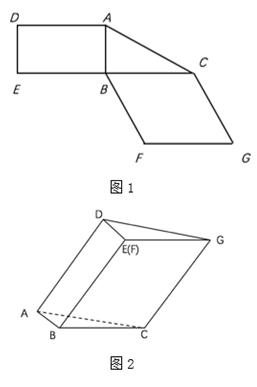 (1)、证明:图2中的A,C,G,D四点共面,且平面ABC⊥平面BCGE;(2)、求图2中的二面角B-CG-A的大小.
(1)、证明:图2中的A,C,G,D四点共面,且平面ABC⊥平面BCGE;(2)、求图2中的二面角B-CG-A的大小.
30. 如图,长方体ABCD–A1B1C1D1的底面ABCD是正方形,点E在棱AA1上,BE⊥EC1.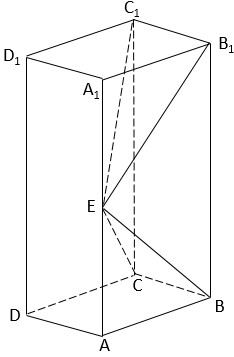 (1)、证明:BE⊥平面EB1C1;(2)、若AE=A1E,求二面角B–EC–C1的正弦值.31. 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,E为CD的中点.
(1)、证明:BE⊥平面EB1C1;(2)、若AE=A1E,求二面角B–EC–C1的正弦值.31. 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,E为CD的中点.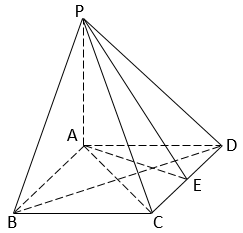
(Ⅰ)求证:BD⊥平面PAC;
(Ⅱ)若∠ABC=60°,求证:平面PAB⊥平面PAE;
(Ⅲ)棱PB上是否存在点F,使得CF∥平面PAE?说明理由.
32. 如图,直四棱柱ABCD-A1B1C1D1的底面是菱形,AA1=4,AB=2, BAD=60°,E,M,N分别是BC,BB1 , A1D的中点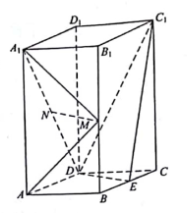 (1)、证明:MN∥平面C1DE;(2)、求二面角A-MA1-N的正弦值。33. 如图,四边形 为正方形, 分别为 的中点,以 为折痕把 折起,使点 到达点 的位置,且 .
(1)、证明:MN∥平面C1DE;(2)、求二面角A-MA1-N的正弦值。33. 如图,四边形 为正方形, 分别为 的中点,以 为折痕把 折起,使点 到达点 的位置,且 .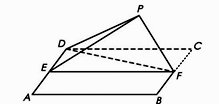 (1)、证明:平面 平面 ;(2)、求 与平面 所成角的正弦值.34. 如图,在四面体ABCD中,△ABC是等边三角形,平面ABC⊥平面ABD , 点M为棱AB的中点,AB=2,AD= ,∠BAD=90°.
(1)、证明:平面 平面 ;(2)、求 与平面 所成角的正弦值.34. 如图,在四面体ABCD中,△ABC是等边三角形,平面ABC⊥平面ABD , 点M为棱AB的中点,AB=2,AD= ,∠BAD=90°.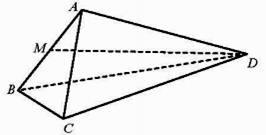
(Ⅰ)求证:AD⊥BC;
(Ⅱ)求异面直线BC与MD所成角的余弦值;
(Ⅲ)求直线CD与平面ABD所成角的正弦值.
35. 如图,在三角锥 中, , , 为 的中点.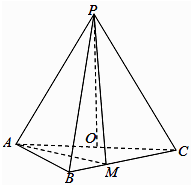 (1)、证明: 平面 ;(2)、若点 在棱 上,且二面角 为 ,求 与平面 所成角的正弦值.
(1)、证明: 平面 ;(2)、若点 在棱 上,且二面角 为 ,求 与平面 所成角的正弦值.

