平面向量——大数据之五年(2018-2022)高考真题汇编(新高考卷与全国理科)
试卷更新日期:2022-07-13 类型:二轮复习
一、单选题
-
1. 已知 ,若 ,则 ( )A、-6 B、-5 C、5 D、62. 已知向量 , 则 ( )A、2 B、3 C、4 D、53. 已知椭圆 的离心率为 , 分别为C的左、右顶点,B为C的上顶点.若 ,则C的方程为( )A、 B、 C、 D、4. 已知向量 满足 ,则 ( )A、-2 B、-1 C、1 D、25. 在 中, , , . 为 所在平面内的动点,且 ,则 的取值范围是( )A、 B、 C、 D、6. 在 中,点D在边AB上, 记 则 ( )A、3-2 B、-2+3 C、3+2 D、2+37. 在平面内,A,B是两个定点,C是动点,若 ,则点C的轨迹为( )A、圆 B、椭圆 C、抛物线 D、直线8. 已知向量a,b满足 , , ,则 ( )A、 B、 C、 D、9. 已知单位向量a,b的夹角为60°,则在下列向量中,与b垂直的是( )A、a+2b B、2a+b C、a–2b D、2a–b10. 已知P是边长为2的正六边形ABCDEF内的一点,则 的取值范围是( )A、 B、 C、 D、11. 已知向量=(2,3),=(3,2),则|-|=( )
A、 B、2 C、5 D、5012. 已知 =(2,3), =(3,t),| |=1,则 =( )
A、-3 B、-2 C、2 D、313. 已知非零向量 , 满足| |=2| |,且 ,则 与 的夹角为( )A、 B、 C、 D、14. 在 中,AD为BC边上的中线,E为AD的中点,则 ( )A、 B、 C、 D、15. 如图,在平面四边形ABCD中, , , , . 若点E为边CD上的动点,则 的最小值为( )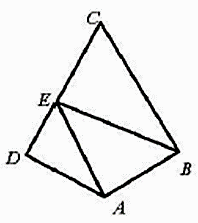 A、 B、 C、 D、16. 已知向量 , 满足=1, ⋅=−1 ,则·(2-)=( )
A、 B、 C、 D、16. 已知向量 , 满足=1, ⋅=−1 ,则·(2-)=( )
A、4 B、3 C、2 D、0二、多选题
-
17. 已知O为坐标原点,过抛物线 的焦点F的直线与C交于A,B两点,点A在第一象限,点 ,若 ,则( )A、直线 的斜率为 B、 C、 D、18. 已知O为坐标原点,点A(1,1)在抛物线C: 上,过点 的直线交C于P,Q两点,则( )A、C的准线为 B、直线AB与C相切 C、 D、19. 已知O为坐标原点,点P1(cosα,sinα),P2(cosβ,-sinβ),P3(cos(α+β),sin(α+β)),A(1,0),则( )A、| = B、 = C、 = D、
三、填空题
-
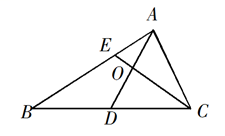
20. 设向量 , 的夹角的余弦值为 ,且 ,则 .21. 已知向量 .若 ,则 .22. 已知向量 , 则 .23. , , ,则 ; .24. 已知向量a=(2,5),b=(λ,4),若 ,则λ=.25. 若向量 满足| |=3,| |=5, ⋅ =1,则| |= .26. 已知向量a=(3,1),b=(1,0), ,若a⊥c,则k=。27. 已知向量 =(1,3),b=(3,4),若( -λ )⊥ , 则λ=。28. 在边长为1的等边三角形ABC中,D为线段BC上的动点, 且交AB于点E . 且交AC于点F , 则 的值为; 的最小值为 .29. 设向量 ,若 ,则 .30. 已知单位向量a,b的夹角为45°,ka–b与a垂直,则k=.31. 设 为单位向量,且 ,则 .32. 如图,在四边形 中, , ,且 ,则实数 的值为 , 若 是线段 上的动点,且 ,则 的最小值为 .
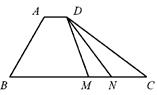 33. 在△ABC中, D在边BC上,延长AD到P,使得AP=9,若 (m为常数),则CD的长度是 .
33. 在△ABC中, D在边BC上,延长AD到P,使得AP=9,若 (m为常数),则CD的长度是 .