基本不等式——大数据之五年(2018-2022)高考真题汇编(新高考卷与全国理科)
试卷更新日期:2022-07-13 类型:二轮复习
一、单选题
-
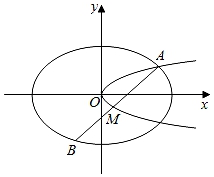
1. 下列函数中最小值为4的是( )A、 B、 C、 D、2. 已知F1 , F2是椭圆C: 的两个焦点,点M在C 上,则|MF1|·|MF2|的最大值为( )A、13 B、12 C、9 D、63. 已知函数f(x)=sinx+ ,则( )A、f(x)的最小值为2 B、f(x)的图像关于y轴对称 C、f(x)的图像关于直线 对称 D、f(x)的图像关于直线 对称
二、多选题
-
4. 对任意x,y, ,则( )A、 B、 C、 D、5. 已知a>0,b>0,且a+b=1,则( )A、 B、 C、 D、6. 信息熵是信息论中的一个重要概念.设随机变量X所有可能的取值为 ,且 ,定义X的信息熵 .( )A、若n=1,则H(X)=0 B、若n=2,则H(X)随着 的增大而增大 C、若 ,则H(X)随着n的增大而增大 D、若n=2m,随机变量Y所有可能的取值为 ,且 ,则H(X)≤H(Y)
三、填空题
-
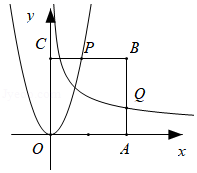
7. 已知 中,点D在边BC上, .当 取得最小值时, .8. 若 ,则 的最小值为 .9. 已知 ,且 ,则 的最小值为 .10. 已知 ,则 的最小值是 .11. 如图,已知正方形 ,其中 ,函数 交 于点 ,函数 交 于点 ,当 最小时,则 的值为 .
 12. 设 ,则 的最小值为.13. 设 ,则 的最小值为.14. 在平面直角坐标系中,已知点A(-1,0),B(2,0),E,F是y轴上的两个动点,且| |=2,则 · 的最小值为15. 已知实数x₁、x₂、y₁、y₂满足: , , ,则 + 的最大值为
12. 设 ,则 的最小值为.13. 设 ,则 的最小值为.14. 在平面直角坐标系中,已知点A(-1,0),B(2,0),E,F是y轴上的两个动点,且| |=2,则 · 的最小值为15. 已知实数x₁、x₂、y₁、y₂满足: , , ,则 + 的最大值为四、解答题
-
16. 已知a,b,c都是正数,且 ,证明:(1)、 ;(2)、 .17. 记 的内角A,B,C的对边分别为a,b,c,已知(1)、若 求B;(2)、求 的最小值.18. 如图,矩形ABCD区域内,D处有一棵古树,为保护古树,以D为圆心,DA为半径划定圆D作为保护区域,已知 m, m,点E为AB上的动点,点F为CD上的动点,满足EF与圆D相切.
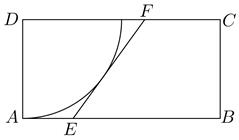 (1)、若∠ADE ,求EF的长;(2)、当点E在AB的什么位置时,梯形FEBC的面积有最大值,最大面积为多少?
(1)、若∠ADE ,求EF的长;(2)、当点E在AB的什么位置时,梯形FEBC的面积有最大值,最大面积为多少?(长度精确到0.1m,面积精确到0.01m²)
19. 设a,b,c R,a+b+c=0,abc=1.(1)、证明:ab+bc+ca<0;(2)、用max{a,b,c}表示a,b,c中的最大值,证明:max{a,b,c}≥ .