2022年中考数学真题分类汇编:23 锐角三角函数
试卷更新日期:2022-07-12 类型:二轮复习
一、单选题
-
1. 如图,某博物馆大厅电梯的截面图中,AB的长为12米,AB与AC的夹角为 ,则高BC是( )
 A、 米 B、 米 C、 米 D、 米2. 如图,在 中, ,将 绕点A逆时针旋转 ,得到 ,连接 并延长交AB于点D,当 时, 的长是( )
A、 米 B、 米 C、 米 D、 米2. 如图,在 中, ,将 绕点A逆时针旋转 ,得到 ,连接 并延长交AB于点D,当 时, 的长是( )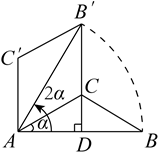 A、 B、 C、 D、3. 如图,在△ABC中,BC=6,AC=8,∠C=90°,以点B为圆心,BC长为半径画弧,与AB交于点D,再分别以A、D为圆心,大于AD的长为半径画弧,两弧交于点M、N,作直线MN,分别交AC、AB于点E、F,则AE的长度为( )
A、 B、 C、 D、3. 如图,在△ABC中,BC=6,AC=8,∠C=90°,以点B为圆心,BC长为半径画弧,与AB交于点D,再分别以A、D为圆心,大于AD的长为半径画弧,两弧交于点M、N,作直线MN,分别交AC、AB于点E、F,则AE的长度为( ) A、 B、3 C、2 D、4. 如图,在正方形方格纸中,每个小正方形的边长都相等,A,B,C,D都在格点处,AB与CD相交于点P,则cos∠APC的值为( )
A、 B、3 C、2 D、4. 如图,在正方形方格纸中,每个小正方形的边长都相等,A,B,C,D都在格点处,AB与CD相交于点P,则cos∠APC的值为( ) A、 B、 C、 D、5. 的值等于( )A、2 B、1 C、 D、6. 如图,等腰△ABC的面积为2 , AB=AC,BC=2.作AE∥BC且AE=BC.点P是线段AB上一动点,连接PE,过点E作PE的垂线交BC的延长线于点F,M是线段EF的中点.那么,当点P从A点运动到B点时,点M的运动路径长为( )
A、 B、 C、 D、5. 的值等于( )A、2 B、1 C、 D、6. 如图,等腰△ABC的面积为2 , AB=AC,BC=2.作AE∥BC且AE=BC.点P是线段AB上一动点,连接PE,过点E作PE的垂线交BC的延长线于点F,M是线段EF的中点.那么,当点P从A点运动到B点时,点M的运动路径长为( )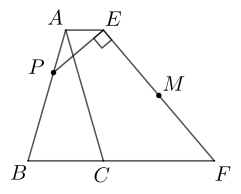 A、 B、3 C、 D、47. 如图,是的高,若 , , 则边的长为( )
A、 B、3 C、 D、47. 如图,是的高,若 , , 则边的长为( ) A、 B、 C、 D、8. 一配电房示意图如图所示,它是一个轴对称图形.已知BC=6m.∠ABC=α.则房顶A离地面EF的高度为( )
A、 B、 C、 D、8. 一配电房示意图如图所示,它是一个轴对称图形.已知BC=6m.∠ABC=α.则房顶A离地面EF的高度为( )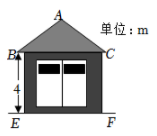 A、 B、 C、 D、9. 家具厂利用如图所示直径为1米的圆形材料加工成一种扇形家具部件,已知扇形的圆心角∠BAC=90°,则扇形部件的面积为( )
A、 B、 C、 D、9. 家具厂利用如图所示直径为1米的圆形材料加工成一种扇形家具部件,已知扇形的圆心角∠BAC=90°,则扇形部件的面积为( )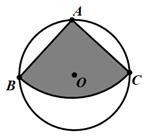 A、 米2 B、 米2 C、 米2 D、 米210. 如图,已知菱形ABCD的边长为4,E是BC的中点,AF平分∠EAD交CD于点F,FG∥AD交AE于点G,若cosB= ,则FG的长是( )
A、 米2 B、 米2 C、 米2 D、 米210. 如图,已知菱形ABCD的边长为4,E是BC的中点,AF平分∠EAD交CD于点F,FG∥AD交AE于点G,若cosB= ,则FG的长是( )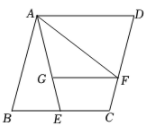 A、3 B、 C、 D、11. 为⊙ 外一点, 与⊙ 相切于点 , , ,则 的长为( )A、 B、5 C、8 D、912. 如图,已知点B,D,C在同一直线的水平,在点C处测得建筑物AB的顶端A的仰角为α,在点D处测得建筑物AB的顶端A的仰角为β, , 则建筑物AB的高度为( )
A、3 B、 C、 D、11. 为⊙ 外一点, 与⊙ 相切于点 , , ,则 的长为( )A、 B、5 C、8 D、912. 如图,已知点B,D,C在同一直线的水平,在点C处测得建筑物AB的顶端A的仰角为α,在点D处测得建筑物AB的顶端A的仰角为β, , 则建筑物AB的高度为( ) A、 B、 C、 D、13. 如图,在中, , , 点D是AC上一点,连接BD.若 , , 则CD的长为( )
A、 B、 C、 D、13. 如图,在中, , , 点D是AC上一点,连接BD.若 , , 则CD的长为( ) A、 B、3 C、 D、214. 如图,已知△ABC内接于半径为1的⊙O,∠BAC=θ(θ是锐角),则△ABC的面积的最大值为( )
A、 B、3 C、 D、214. 如图,已知△ABC内接于半径为1的⊙O,∠BAC=θ(θ是锐角),则△ABC的面积的最大值为( )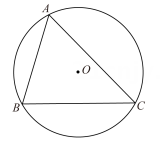 A、cosθ(1+cosθ) B、cosθ(1+sinθ) C、sinθ(1+sinθ) D、sinθ(1+cosθ)15. 下列计算结果,正确的是( )A、 B、 C、 D、
A、cosθ(1+cosθ) B、cosθ(1+sinθ) C、sinθ(1+sinθ) D、sinθ(1+cosθ)15. 下列计算结果,正确的是( )A、 B、 C、 D、二、填空题
-
16. 喜迎二十大,“龙舟故里”赛龙舟.丹丹在汩罗江国际龙舟竞渡中心广场点处观看200米直道竞速赛.如图所示,赛道为东西方向,赛道起点位于点的北偏西方向上,终点位于点的北偏东方向上,米,则点到赛道的距离约为米(结果保留整数,参考数据:).
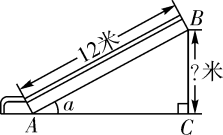
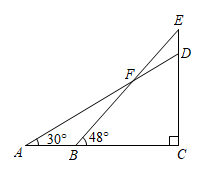
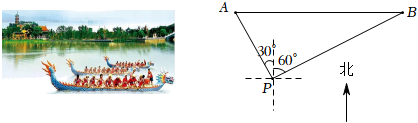 17. 如图,校园内有一株枯死的大树 , 距树12米处有一栋教学楼 , 为了安全,学校决定砍伐该树,站在楼顶处,测得点的仰角为45°,点的俯角为30°,小青计算后得到如下结论:①米;②米;③若直接从点处砍伐,树干倒向教学楼方向会对教学楼有影响;④若第一次在距点的8米处的树干上砍伐,不会对教学楼造成危害.其中正确的是.(填写序号,参考数值: , )
17. 如图,校园内有一株枯死的大树 , 距树12米处有一栋教学楼 , 为了安全,学校决定砍伐该树,站在楼顶处,测得点的仰角为45°,点的俯角为30°,小青计算后得到如下结论:①米;②米;③若直接从点处砍伐,树干倒向教学楼方向会对教学楼有影响;④若第一次在距点的8米处的树干上砍伐,不会对教学楼造成危害.其中正确的是.(填写序号,参考数值: , )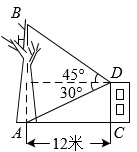 18. 如图, 岛在A岛的北偏东 方向, 岛在 岛的北偏西 方向,则 的大小是.
18. 如图, 岛在A岛的北偏东 方向, 岛在 岛的北偏西 方向,则 的大小是.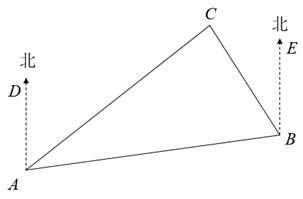 19. 菱形的边长为2, , 点、分别是、上的动点,的最小值为.
19. 菱形的边长为2, , 点、分别是、上的动点,的最小值为.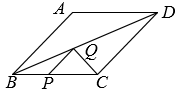 20. 如图,有甲乙两座建筑物,从甲建筑物点处测得乙建筑物点的俯角为 , 点的俯角为 , 为两座建筑物的水平距离.已知乙建筑物的高度为 , 则甲建筑物的高度为.( , , , 结果保留整数).
20. 如图,有甲乙两座建筑物,从甲建筑物点处测得乙建筑物点的俯角为 , 点的俯角为 , 为两座建筑物的水平距离.已知乙建筑物的高度为 , 则甲建筑物的高度为.( , , , 结果保留整数).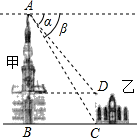
三、解答题
-
21. 如图所示,为了测量百货大楼顶部广告牌的高度,在距离百货大楼30m的A处用仪器测得;向百货大楼的方向走10m,到达B处时,测得 , 仪器高度忽略不计,求广告牌的高度.(结果保留小数点后一位)
(参考数据: , , , )
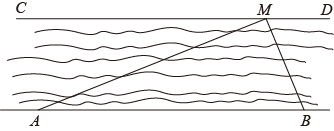
 22. 小军同学想利用所学的“锐角三角函数”知识测量一段两岸平行的河流宽度.他先在河岸设立A,B两个观测点,然后选定对岸河边的一棵树记为点M.测得AB=50m,∠MAB=22°,∠MBA=67°.请你依据所测数据求出这段河流的宽度(结果精确到0.1m).
22. 小军同学想利用所学的“锐角三角函数”知识测量一段两岸平行的河流宽度.他先在河岸设立A,B两个观测点,然后选定对岸河边的一棵树记为点M.测得AB=50m,∠MAB=22°,∠MBA=67°.请你依据所测数据求出这段河流的宽度(结果精确到0.1m).参考数据:sin22°≈ , cos22°≈ , tan22°≈ , sin67°≈ , cos67°≈ , tan67°≈ .
 23. 宜宾东楼始建于唐代,重建于宜宾建城2200周年之际的2018年,新建成的东楼(如图1)成为长江首城会客厅、旅游休闲目的地、文化地标打卡地.某数学小组为测量东楼的高度,在梯步处(如图2)测得楼顶的仰角为 , 沿坡比为7:24的斜坡前行25米到达平台处,测得楼顶的仰角为 , 求东楼的高度DE.(结果精确到1米.参考数据: , )
23. 宜宾东楼始建于唐代,重建于宜宾建城2200周年之际的2018年,新建成的东楼(如图1)成为长江首城会客厅、旅游休闲目的地、文化地标打卡地.某数学小组为测量东楼的高度,在梯步处(如图2)测得楼顶的仰角为 , 沿坡比为7:24的斜坡前行25米到达平台处,测得楼顶的仰角为 , 求东楼的高度DE.(结果精确到1米.参考数据: , )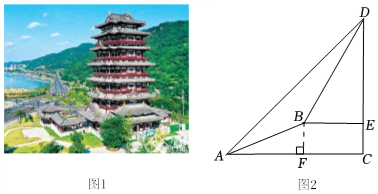 24. 随着科技的发展,无人机已广泛应用于生产和生活,如代替人们在高空测量距离和角度.某校“综合与实践”活动小组的同学要测星AB,CD两座楼之间的距离,他们借助无人机设计了如下测量方案:无人机在AB,CD两楼之间上方的点O处,点O距地面AC的高度为60m,此时观测到楼AB底部点A处的俯角为70°,楼CD上点E处的俯角为30°,沿水平方向由点O飞行24m到达点F,测得点E处俯角为60°,其中点A,B,C,D,E,F,O均在同一竖直平面内.请根据以上数据求楼AB与CD之间的距离AC的长(结果精确到1m.参考数据:).
24. 随着科技的发展,无人机已广泛应用于生产和生活,如代替人们在高空测量距离和角度.某校“综合与实践”活动小组的同学要测星AB,CD两座楼之间的距离,他们借助无人机设计了如下测量方案:无人机在AB,CD两楼之间上方的点O处,点O距地面AC的高度为60m,此时观测到楼AB底部点A处的俯角为70°,楼CD上点E处的俯角为30°,沿水平方向由点O飞行24m到达点F,测得点E处俯角为60°,其中点A,B,C,D,E,F,O均在同一竖直平面内.请根据以上数据求楼AB与CD之间的距离AC的长(结果精确到1m.参考数据:).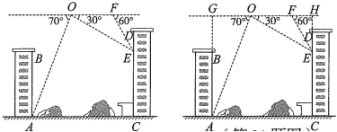 25. “体育承载着国家强盛、民族振兴的梦想”.墩墩使用握力器(如实物图所示)锻炼手部肌肉.如图,握力器弹簧的一端固定在点处,在无外力作用下,弹簧的长度为 , 即.开始训练时,将弹簧的端点调在点处,此时弹簧长 , 弹力大小是 , 经过一段时间的锻炼后,他手部的力量大大提高,需增加训练强度,于是将弹簧端点调到点处,使弹力大小变为 , 已知 , 求的长.
25. “体育承载着国家强盛、民族振兴的梦想”.墩墩使用握力器(如实物图所示)锻炼手部肌肉.如图,握力器弹簧的一端固定在点处,在无外力作用下,弹簧的长度为 , 即.开始训练时,将弹簧的端点调在点处,此时弹簧长 , 弹力大小是 , 经过一段时间的锻炼后,他手部的力量大大提高,需增加训练强度,于是将弹簧端点调到点处,使弹力大小变为 , 已知 , 求的长.注:弹簧的弹力与形变成正比,即 , 是劲度系数,是弹簧的形变量,在无外力作用下,弹簧的长度为 , 在外力作用下,弹簧的长度为 , 则.