2022年中考数学真题分类汇编:22 图形的相似
试卷更新日期:2022-07-12 类型:二轮复习
一、单选题
-
1. 如图,点 , 将线段平移得到线段 , 若 , 则点D的坐标是( )
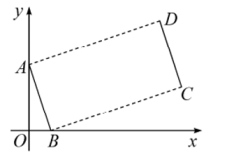 A、 B、 C、 D、2. 在△ABC中(如图),点D、E分别为AB、AC的中点,则S△ADE:S△ABC=( )
A、 B、 C、 D、2. 在△ABC中(如图),点D、E分别为AB、AC的中点,则S△ADE:S△ABC=( )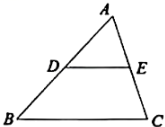 A、1:1 B、1:2 C、1:3 D、1:43. 如图所示,在菱形中,对角线与相交于点 , 过点作交的延长线于点 , 下列结论不一定正确的是( )
A、1:1 B、1:2 C、1:3 D、1:43. 如图所示,在菱形中,对角线与相交于点 , 过点作交的延长线于点 , 下列结论不一定正确的是( )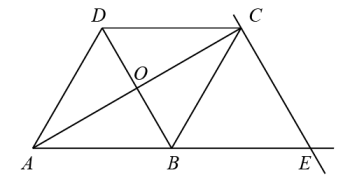 A、 B、是直角三角形 C、 D、4. 如图,在四边形 中, , , , 平分 .设 , ,则 关于 的函数关系用图象大致可以表示为( )
A、 B、是直角三角形 C、 D、4. 如图,在四边形 中, , , , 平分 .设 , ,则 关于 的函数关系用图象大致可以表示为( )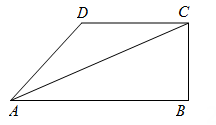 A、
A、 B、
B、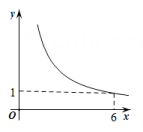 C、
C、 D、
D、 5. 在设计人体雕像时,使雕像上部(腰部以上)与下部(腰部以下)的高度比,等于下部与全部的高度比,可以增加视觉美感.如图,按此比例设计一座高度为2m 的雷锋雕像,那么该雕像的下部设计高度约是( )(结果精确到 .参考数据: , , )
5. 在设计人体雕像时,使雕像上部(腰部以上)与下部(腰部以下)的高度比,等于下部与全部的高度比,可以增加视觉美感.如图,按此比例设计一座高度为2m 的雷锋雕像,那么该雕像的下部设计高度约是( )(结果精确到 .参考数据: , , ) A、 B、 C、 D、6. 如图,在 △ABC中,D、E分别为线段BC、BA的中点,设△ABC的面积为S1 , △EBD的面积为S2 . 则 =( )
A、 B、 C、 D、6. 如图,在 △ABC中,D、E分别为线段BC、BA的中点,设△ABC的面积为S1 , △EBD的面积为S2 . 则 =( ) A、 B、 C、 D、7. 若 , , ,则 ( )A、 B、 C、 D、8. 将一张以AB为边的矩形纸片,先沿一条直线剪掉一个直角三角形,在剩下的纸片中,再沿一条直线剪掉一个直角三角形(剪掉的两个直角三角形相似),剩下的是如图所示的四边形纸片 ,其中 , , , , ,则剪掉的两个直角三角形的斜边长不可能是( )
A、 B、 C、 D、7. 若 , , ,则 ( )A、 B、 C、 D、8. 将一张以AB为边的矩形纸片,先沿一条直线剪掉一个直角三角形,在剩下的纸片中,再沿一条直线剪掉一个直角三角形(剪掉的两个直角三角形相似),剩下的是如图所示的四边形纸片 ,其中 , , , , ,则剪掉的两个直角三角形的斜边长不可能是( ) A、 B、 C、10 D、9. 如图,点E在矩形 的 边上,将 沿 翻折,点A恰好落在 边上的点F处,若 , ,则 的长为( )
A、 B、 C、10 D、9. 如图,点E在矩形 的 边上,将 沿 翻折,点A恰好落在 边上的点F处,若 , ,则 的长为( ) A、9 B、12 C、15 D、1810. 如图,将矩形 沿着 、 、 翻折,使得点 、 、 恰好都落在点 处,且点 、 、 在同一条直线上,同时点 、 、 在另一条直线上.小炜同学得出以下结论:
A、9 B、12 C、15 D、1810. 如图,将矩形 沿着 、 、 翻折,使得点 、 、 恰好都落在点 处,且点 、 、 在同一条直线上,同时点 、 、 在另一条直线上.小炜同学得出以下结论:① ;② ;③ ;④ ;⑤ .
其中正确的是( )
 A、①②③ B、①③④ C、①④⑤ D、②③④11. △ABC的三边长分别为2,3,4,另有一个与它相似的三角形 DEF ,其最长边为12,则 △DEF的周长是( )A、54 B、36 C、27 D、2112. 如图,D,E,F分别是△ABC三边上的点,其中BC=8,BC边上的高为6,且DE∥BC,则△DEF面积的最大值为( )
A、①②③ B、①③④ C、①④⑤ D、②③④11. △ABC的三边长分别为2,3,4,另有一个与它相似的三角形 DEF ,其最长边为12,则 △DEF的周长是( )A、54 B、36 C、27 D、2112. 如图,D,E,F分别是△ABC三边上的点,其中BC=8,BC边上的高为6,且DE∥BC,则△DEF面积的最大值为( ) A、6 B、8 C、10 D、1213. 如图,正方形ABCD与正方形BEFG有公共顶点B,连接EC、GA,交于点O,GA与BC交于点P,连接OD、OB,则下列结论一定正确的是( )
A、6 B、8 C、10 D、1213. 如图,正方形ABCD与正方形BEFG有公共顶点B,连接EC、GA,交于点O,GA与BC交于点P,连接OD、OB,则下列结论一定正确的是( )①EC⊥AG;②△OBP∽△CAP;③OB平分∠CBG;④∠AOD=45°;
 A、①③ B、①②③ C、②③ D、①②④14. 如图,在△ABC中,点D、E分别在边AB、AC上,若DE∥BC, ,DE=6cm,则BC的长为( )
A、①③ B、①②③ C、②③ D、①②④14. 如图,在△ABC中,点D、E分别在边AB、AC上,若DE∥BC, ,DE=6cm,则BC的长为( ) A、9cm B、12cm C、15cm D、18cm15. 如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的三个点A,B,C都在横线上:若线段AB=3,则线段BC的长是( )
A、9cm B、12cm C、15cm D、18cm15. 如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的三个点A,B,C都在横线上:若线段AB=3,则线段BC的长是( ) A、 B、1 C、 D、2
A、 B、1 C、 D、2二、填空题
-
16. 古希腊数学家泰勒斯曾利用立杆测影的方法,在金字塔影子的顶部直立一根木杆,借助太阳光测金字塔的高度.如图,木杆EF长2米,它的影长FD是4米,同一时刻测得OA是268米,则金字塔的高度BO是米.
 17. 在矩形ABCD中, , , 点E在边CD上,且 , 点P是直线BC上的一个动点.若是直角三角形,则BP的长为 .18. 如图,中,点、分别在边、上,若 , , , 则.
17. 在矩形ABCD中, , , 点E在边CD上,且 , 点P是直线BC上的一个动点.若是直角三角形,则BP的长为 .18. 如图,中,点、分别在边、上,若 , , , 则.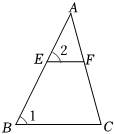 19. 如图1,在中, , 动点从点出发,沿折线匀速运动至点停止.若点的运动速度为 , 设点的运动时间为 , 的长度为 , 与的函数图象如图2所示.当恰好平分时的值为.
19. 如图1,在中, , 动点从点出发,沿折线匀速运动至点停止.若点的运动速度为 , 设点的运动时间为 , 的长度为 , 与的函数图象如图2所示.当恰好平分时的值为. 20. 九年级融融陪同父母选购家装木地板,她感觉某品牌木地板拼接图(如实物图)比较美观,通过手绘(如图)、测量、计算发现点是的黄金分割点,即.延长与相交于点 , 则.(精确到0.001)
20. 九年级融融陪同父母选购家装木地板,她感觉某品牌木地板拼接图(如实物图)比较美观,通过手绘(如图)、测量、计算发现点是的黄金分割点,即.延长与相交于点 , 则.(精确到0.001)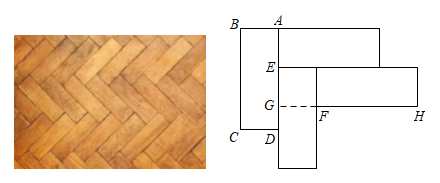
三、综合题
-
21. 如图1,抛物线经过点 , 并交x轴于另一点B,点在第一象限的抛物线上,交直线于点D.
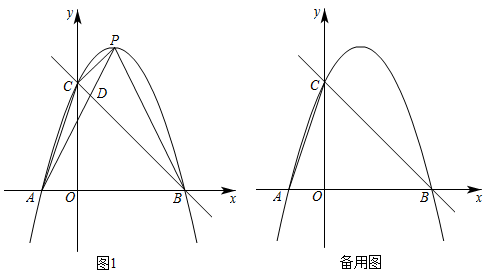 (1)、求该抛物线的函数表达式;(2)、当点P的坐标为时,求四边形的面积;(3)、点Q在抛物线上,当的值最大且是直角三角形时,求点Q的横坐标;22. 某数学兴趣小组运用《几何画板》软件探究y=ax2(a>0)型抛物线图象.发现:如图1所示,该类型图象上任意一点M到定点 F(0,)的距离MF,始终等于它到定直线l:y=﹣上的距离MN(该结论不需要证明),他们称:定点F为图象的焦点,定直线l为图象的准线,y=﹣叫做抛物线的准线方程.其中原点O为FH的中点,FH=2OF= , 例如,抛物线y=x2 , 其焦点坐标为F(0,),准线方程为l:y=﹣.其中MF=MN,FH=2OH=1.
(1)、求该抛物线的函数表达式;(2)、当点P的坐标为时,求四边形的面积;(3)、点Q在抛物线上,当的值最大且是直角三角形时,求点Q的横坐标;22. 某数学兴趣小组运用《几何画板》软件探究y=ax2(a>0)型抛物线图象.发现:如图1所示,该类型图象上任意一点M到定点 F(0,)的距离MF,始终等于它到定直线l:y=﹣上的距离MN(该结论不需要证明),他们称:定点F为图象的焦点,定直线l为图象的准线,y=﹣叫做抛物线的准线方程.其中原点O为FH的中点,FH=2OF= , 例如,抛物线y=x2 , 其焦点坐标为F(0,),准线方程为l:y=﹣.其中MF=MN,FH=2OH=1.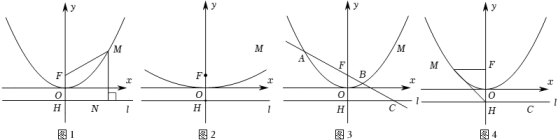 (1)、【基础训练】
(1)、【基础训练】请分别直接写出抛物线y=2x2的焦点坐标和准线l的方程: , .
(2)、【技能训练】如图2所示,已知抛物线y=x2上一点P到准线l的距离为6,求点P的坐标;
(3)、【能力提升】如图3所示,已知过抛物线y=ax2(a>0)的焦点F的直线依次交抛物线及准线l于点A、B、C.若BC=2BF,AF=4,求a的值;
(4)、【拓展升华】古希腊数学家欧多克索斯在深入研究比例理论时,提出了分线段的“中末比”问题:点C将一条线段AB分为两段AC和CB,使得其中较长一段AC是全线段AB与另一段CB的比例中项,即满足:==.后人把这个数称为“黄金分割”把点C称为线段AB的黄金分割点.
如图4所示,抛物线y=x2的焦点F(0,1),准线l与y轴交于点H(0,﹣1),E为线段HF的黄金分割点,点M为y轴左侧的抛物线上一点.当=时,请直接写出△HME的面积值.
23. 如图,和的顶点重合, , , , .

 (1)、特例发现:如图1,当点 , 分别在 , 上时,可以得出结论: , 直线与直线的位置关系是;(2)、探究证明:如图2,将图1中的绕点顺时针旋转,使点恰好落在线段上,连接 , (1)中的结论是否仍然成立?若成立,请证明;若不成立,请说明理由;(3)、拓展运用:如图3,将图1中的绕点顺时针旋转 , 连接、 , 它们的延长线交于点 , 当时,求的值.24. 回顾:用数学的思维思考
(1)、特例发现:如图1,当点 , 分别在 , 上时,可以得出结论: , 直线与直线的位置关系是;(2)、探究证明:如图2,将图1中的绕点顺时针旋转,使点恰好落在线段上,连接 , (1)中的结论是否仍然成立?若成立,请证明;若不成立,请说明理由;(3)、拓展运用:如图3,将图1中的绕点顺时针旋转 , 连接、 , 它们的延长线交于点 , 当时,求的值.24. 回顾:用数学的思维思考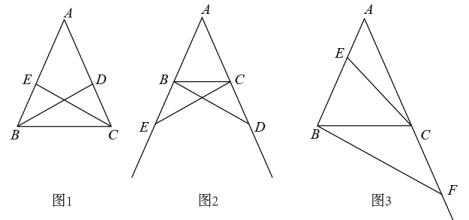 (1)、如图1,在△ABC中,AB=AC.
(1)、如图1,在△ABC中,AB=AC.①BD,CE是△ABC的角平分线.求证:BD=CE.
②点D,E分别是边AC,AB的中点,连接BD,CE.求证:BD=CE.
(从①②两题中选择一题加以证明)
(2)、猜想:用数学的眼光观察经过做题反思,小明同学认为:在△ABC中,AB=AC,D为边AC上一动点(不与点A,C重合).对于点D在边AC上的任意位置,在另一边AB上总能找到一个与其对应的点E,使得BD=CE.进而提出问题:若点D,E分别运动到边AC,AB的延长线上,BD与CE还相等吗?请解决下面的问题:
如图2,在△ABC中,AB=AC,点D,E分别在边AC,AB的延长线上,请添加一个条件(不再添加新的字母),使得BD=CE,并证明.
(3)、探究:用数学的语言表达如图3,在△ABC中,AB=AC=2,∠A=36°,E为边AB上任意一点(不与点A,B重合),F为边AC延长线上一点.判断BF与CE能否相等.若能,求CF的取值范围;若不能,说明理由.
25. 如图,某水渠的横断面是以AB为直径的半圆O , 其中水面截线 .嘉琪在A处测得垂直站立于B处的爸爸头顶C的仰角为14°,点M的俯角为7°.已知爸爸的身高为1.7m .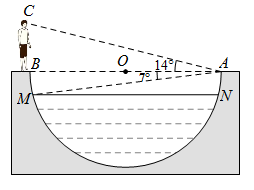 (1)、求∠C的大小及AB的长;(2)、请在图中画出线段DH , 用其长度表示最大水深(不说理由),并求最大水深约为多少米(结果保留小数点后一位).(参考数据: 取4, 取4.1)
(1)、求∠C的大小及AB的长;(2)、请在图中画出线段DH , 用其长度表示最大水深(不说理由),并求最大水深约为多少米(结果保留小数点后一位).(参考数据: 取4, 取4.1)