2022年中考数学真题分类汇编:21 平移、旋转变换
试卷更新日期:2022-07-12 类型:二轮复习
一、单选题
-
1. 2022北京冬残奥会的会徽是以汉字“飞”为灵感来设计的,展现了运动员不断飞跃,超越自我,奋力拼搏,激励世界的冬残奥精神下列的四个图中,能由如图所示的会徽经过平移得到的是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 如图,在 中, ,将 绕点A逆时针旋转 ,得到 ,连接 并延长交AB于点D,当 时, 的长是( )
2. 如图,在 中, ,将 绕点A逆时针旋转 ,得到 ,连接 并延长交AB于点D,当 时, 的长是( )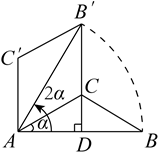 A、 B、 C、 D、3. 在平面直角坐标系中,点关于原点对称的点的坐标是( )A、 B、 C、 D、4. 如图,点 , 将线段平移得到线段 , 若 , 则点D的坐标是( )
A、 B、 C、 D、3. 在平面直角坐标系中,点关于原点对称的点的坐标是( )A、 B、 C、 D、4. 如图,点 , 将线段平移得到线段 , 若 , 则点D的坐标是( )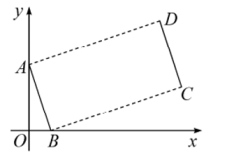 A、 B、 C、 D、5. 下面四个交通标志中,是中心对称图形的是( )A、
A、 B、 C、 D、5. 下面四个交通标志中,是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 6. 如图,和都是等腰直角三角形, , 点是边上的动点(不与点B、C重合),与交于点 , 连结下列结论:;;若 , 则;在内存在唯一一点 , 使得的值最小,若点在的延长线上,且的长为2,则其中含所有正确结论的选项是( )
6. 如图,和都是等腰直角三角形, , 点是边上的动点(不与点B、C重合),与交于点 , 连结下列结论:;;若 , 则;在内存在唯一一点 , 使得的值最小,若点在的延长线上,且的长为2,则其中含所有正确结论的选项是( )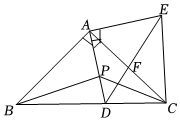 A、 B、 C、 D、7. 如图,点A的坐标为 ,点B是x轴正半轴上的一点,将线段AB绕点A按逆时针方向旋转60°得到线段AC.若点C的坐标为 ,则m的值为( )
A、 B、 C、 D、7. 如图,点A的坐标为 ,点B是x轴正半轴上的一点,将线段AB绕点A按逆时针方向旋转60°得到线段AC.若点C的坐标为 ,则m的值为( )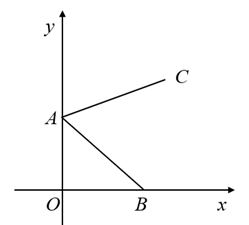 A、 B、 C、 D、8. 如图,在中, , , 将绕点顺时针旋转得到 , 点A、B的对应点分别是 , , 点是边的中点,连接 , , .则下列结论错误的是( )
A、 B、 C、 D、8. 如图,在中, , , 将绕点顺时针旋转得到 , 点A、B的对应点分别是 , , 点是边的中点,连接 , , .则下列结论错误的是( )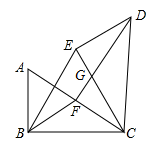 A、 B、 , C、 D、9. 如图,在△ABC中,AB=AC,若M是BC边上任意一点,将△ABM绕点A逆时针旋转得到△ACN,点M的对应点为点N,连接MN,则下列结论一定正确的是( )
A、 B、 , C、 D、9. 如图,在△ABC中,AB=AC,若M是BC边上任意一点,将△ABM绕点A逆时针旋转得到△ACN,点M的对应点为点N,连接MN,则下列结论一定正确的是( )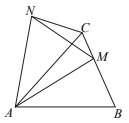 A、 B、 C、 D、10. 如图,四边形为正方形,将绕点逆时针旋转至 , 点 , , 在同一直线上,与交于点 , 延长与的延长线交于点 , , .以下结论:
A、 B、 C、 D、10. 如图,四边形为正方形,将绕点逆时针旋转至 , 点 , , 在同一直线上,与交于点 , 延长与的延长线交于点 , , .以下结论:①;②;③;④.其中正确结论的个数为( )
 A、1个 B、2个 C、3个 D、4个11. 如图,△ABC沿BC方向平移后的像为△DEF,已知BC=5,EC=2,则平移的距离是( )
A、1个 B、2个 C、3个 D、4个11. 如图,△ABC沿BC方向平移后的像为△DEF,已知BC=5,EC=2,则平移的距离是( )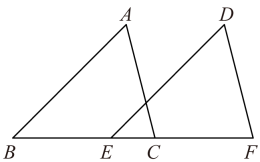 A、1 B、2 C、3 D、412. 如图,在中, , 将以点为中心逆时针旋转得到 , 点在边上,交于点.下列结论:①;②平分;③ , 其中所有正确结论的序号是( )
A、1 B、2 C、3 D、412. 如图,在中, , 将以点为中心逆时针旋转得到 , 点在边上,交于点.下列结论:①;②平分;③ , 其中所有正确结论的序号是( )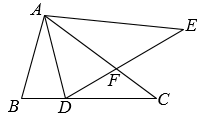 A、①② B、②③ C、①③ D、①②③13. “方胜”是中国古代妇女的一种发饰,其图案由两个全等正方形相叠组成,寓意是同心吉祥.如图,将边长为2cm的正方形ABCD沿对角线BD方向平移1cm得到正方形A′B′C′D′,形成一个“方胜”图案,则点D,B′之间的距离为( )
A、①② B、②③ C、①③ D、①②③13. “方胜”是中国古代妇女的一种发饰,其图案由两个全等正方形相叠组成,寓意是同心吉祥.如图,将边长为2cm的正方形ABCD沿对角线BD方向平移1cm得到正方形A′B′C′D′,形成一个“方胜”图案,则点D,B′之间的距离为( )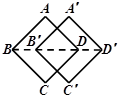 A、1cm B、2cm C、( -1)c. D、(2 -1)cm14. 如图,将△ABC沿BC方向平移1cm 得到对应的△A'B'C'.若B'C=2cm,则BC'的长是( )
A、1cm B、2cm C、( -1)c. D、(2 -1)cm14. 如图,将△ABC沿BC方向平移1cm 得到对应的△A'B'C'.若B'C=2cm,则BC'的长是( )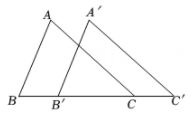 A、2cm B、3cm C、4cm D、5cm15. 如图,在平面直角坐标系中,已知点P(0,2),点A(4,2).以点P为旋转中心,把点A按逆时针方向旋转60°,得点B.在M1( ,0),M2( ,-1),M3(1,4),M4(2, )四个点中,直线PB经过的点是( )
A、2cm B、3cm C、4cm D、5cm15. 如图,在平面直角坐标系中,已知点P(0,2),点A(4,2).以点P为旋转中心,把点A按逆时针方向旋转60°,得点B.在M1( ,0),M2( ,-1),M3(1,4),M4(2, )四个点中,直线PB经过的点是( ) A、M1 B、M2 C、M3 D、M4
A、M1 B、M2 C、M3 D、M4二、填空题
-
16. 如图,点 , , 都在方格纸的格点上, 绕点 顺时针方向旋转 后得到 ,则点 运动的路径 的长为.
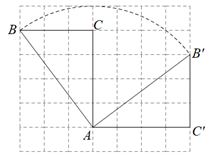 17. 如图,已知等腰的顶角的大小为 , 点D为边上的动点(与、不重合),将绕点A沿顺时针方向旋转角度时点落在处,连接.给出下列结论:①;②;③当时,的面积取得最小值.其中正确的结论有(填结论对应的序号).
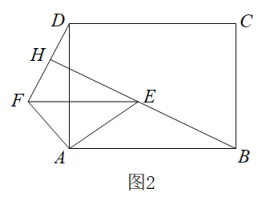
17. 如图,已知等腰的顶角的大小为 , 点D为边上的动点(与、不重合),将绕点A沿顺时针方向旋转角度时点落在处,连接.给出下列结论:①;②;③当时,的面积取得最小值.其中正确的结论有(填结论对应的序号).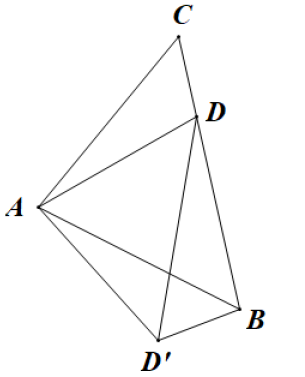 18. 如图1,在矩形ABCD中, , , E,F分别为AB,AD的中点,连接EF.如图2,将△AEF绕点A逆时针旋转角 , 使 , 连接BE并延长交DF于点H,则∠BHD的度数为 , DH的长为.
18. 如图1,在矩形ABCD中, , , E,F分别为AB,AD的中点,连接EF.如图2,将△AEF绕点A逆时针旋转角 , 使 , 连接BE并延长交DF于点H,则∠BHD的度数为 , DH的长为.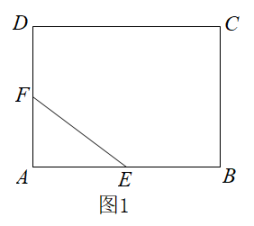
 19. 已知点A(﹣2,b)与点B(a,3)关于原点对称,则a﹣b =.20. 如图, △ABC的边BC长为4cm.将△ABC平移2cm得到△A′B′C′ ,且BB′⊥BC,则阴影部分的面积为 .
19. 已知点A(﹣2,b)与点B(a,3)关于原点对称,则a﹣b =.20. 如图, △ABC的边BC长为4cm.将△ABC平移2cm得到△A′B′C′ ,且BB′⊥BC,则阴影部分的面积为 .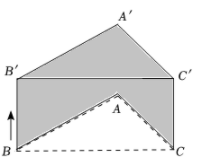
三、作图题
-
21. 如图是由小正方形组成的9×6网格,每个小正方形的顶点叫做格点.△ABC的三个顶点都是格点.仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.
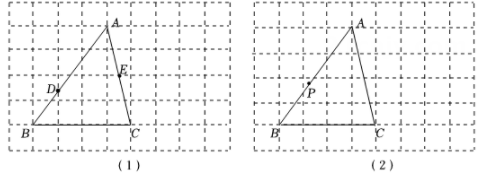 (1)、在图(1)中, , 分别是边 , 与网格线的交点.先将点绕点旋转得到点 , 画出点 , 再在上画点 , 使;(2)、在图(2)中,是边上一点,.先将绕点逆时针旋转 , 得到线段 , 画出线段 , 再画点 , 使 , 两点关于直线对称.22. 如图,在由边长为1个单位长度的小正方形组成的网格中,△ABC的顶点均为格点(网格线的交点).
(1)、在图(1)中, , 分别是边 , 与网格线的交点.先将点绕点旋转得到点 , 画出点 , 再在上画点 , 使;(2)、在图(2)中,是边上一点,.先将绕点逆时针旋转 , 得到线段 , 画出线段 , 再画点 , 使 , 两点关于直线对称.22. 如图,在由边长为1个单位长度的小正方形组成的网格中,△ABC的顶点均为格点(网格线的交点). (1)、将△ABC向上平移6个单位,再向右平移2个单位,得到 , 请画出﹔(2)、以边AC的中点O为旋转中心,将△ABC按逆时针方向旋转180°,得到 , 请画出 .23. 如图,在 2×6 的方格纸中,已知格点P,请按要求画格点图形(顶点均在格点上).
(1)、将△ABC向上平移6个单位,再向右平移2个单位,得到 , 请画出﹔(2)、以边AC的中点O为旋转中心,将△ABC按逆时针方向旋转180°,得到 , 请画出 .23. 如图,在 2×6 的方格纸中,已知格点P,请按要求画格点图形(顶点均在格点上).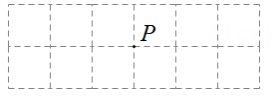
注:图1,图2在答题纸上.
(1)、在图1中画一个锐角三角形,使P为其中一边的中点,再画出该三角形向右平移2个单位后的图形.(2)、在图2中画一个以P为一个顶点的钝角三角形,使三边长都不相等,再画出该三角形绕点P旋转 180° 后的图形.24. 如图,在6×6的方格纸中,点A,B,C均在格点上,试按要求画出相应格点图形,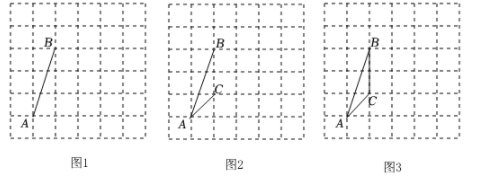 (1)、如图1,作一条线段,使它是AB向右平移一格后的图形;(2)、如图2,作一个轴对称图形,使AB和AC是它的两条边;(3)、如图3,作一个与△ABC相似的三角形,相似比不等于1.
(1)、如图1,作一条线段,使它是AB向右平移一格后的图形;(2)、如图2,作一个轴对称图形,使AB和AC是它的两条边;(3)、如图3,作一个与△ABC相似的三角形,相似比不等于1.四、综合题
-
25. 综合与实践
数学是以数量关系和空间形式为主要研究对象的科学.数学实践活动有利于我们在图形运动变化的过程中去发现其中的位置关系和数量关系,让我们在学习与探索中发现数学的美,体会数学实践活动带给我们的乐趣.
如图①,在矩形ABCD中,点E、F、G分别为边BC、AB、AD的中点,连接EF、DF,H为DF的中点,连接GH.将△BEF绕点B旋转,线段DF、GH和CE的位置和长度也随之变化.当△BEF绕点B顺时针旋转90°时,请解决下列问题:
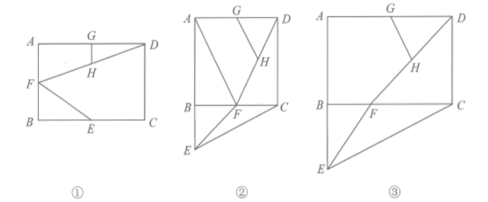
 (1)、图②中,AB=BC,此时点E落在AB的延长线上,点F落在线段BC上,连接AF,猜想GH与CE之间的数量关系,并证明你的猜想;(2)、图③中,AB=2,BC=3,则 ;(3)、当AB=m , BC=n时. .(4)、在(2)的条件下,连接图③中矩形的对角线AC,并沿对角线AC剪开,得△ABC(如图④).点M、N分别在AC、BC上,连接MN,将△CMN沿 MN翻折,使点C的对应点P落在AB的延长线上,若PM平分∠APN,则CM长为 .26. 如图,点 在抛物线C: 上,且在C的对称轴右侧.
(1)、图②中,AB=BC,此时点E落在AB的延长线上,点F落在线段BC上,连接AF,猜想GH与CE之间的数量关系,并证明你的猜想;(2)、图③中,AB=2,BC=3,则 ;(3)、当AB=m , BC=n时. .(4)、在(2)的条件下,连接图③中矩形的对角线AC,并沿对角线AC剪开,得△ABC(如图④).点M、N分别在AC、BC上,连接MN,将△CMN沿 MN翻折,使点C的对应点P落在AB的延长线上,若PM平分∠APN,则CM长为 .26. 如图,点 在抛物线C: 上,且在C的对称轴右侧.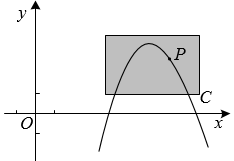 (1)、写出C的对称轴和y的最大值,并求a的值;(2)、坐标平面上放置一透明胶片,并在胶片上描画出点P及C的一段,分别记为 , .平移该胶片,使 所在抛物线对应的函数恰为 .求点 移动的最短路程.
(1)、写出C的对称轴和y的最大值,并求a的值;(2)、坐标平面上放置一透明胶片,并在胶片上描画出点P及C的一段,分别记为 , .平移该胶片,使 所在抛物线对应的函数恰为 .求点 移动的最短路程.