2022年中考数学真题分类汇编:20 轴对称变换
试卷更新日期:2022-07-12 类型:二轮复习
一、单选题
-
1. 孙权于公元221年4月自公安“都鄂”,在西山东麓营建吴王城,并取“以武而昌”之意,改鄂县为武昌,下面四个汉字中,可以看作是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 图1是光的反射规律示意图.其中,PO是入射光线,OQ是反射光线,法线KO⊥MN,∠POK是入射角,∠KOQ是反射角,∠KOQ=∠POK.图2中,光线自点P射入,经镜面EF反射后经过的点是( )
2. 图1是光的反射规律示意图.其中,PO是入射光线,OQ是反射光线,法线KO⊥MN,∠POK是入射角,∠KOQ是反射角,∠KOQ=∠POK.图2中,光线自点P射入,经镜面EF反射后经过的点是( ) A、A点 B、B点 C、C点 D、D点3. 下列命题中是假命题的是( )A、三角形的中位线平行于三角形的第三边,并且等于第三边的一半 B、如果两个角互为邻补角,那么这两个角一定相等 C、从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角 D、直角三角形斜边上的中线等于斜边的一半4. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
A、A点 B、B点 C、C点 D、D点3. 下列命题中是假命题的是( )A、三角形的中位线平行于三角形的第三边,并且等于第三边的一半 B、如果两个角互为邻补角,那么这两个角一定相等 C、从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角 D、直角三角形斜边上的中线等于斜边的一半4. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 5. 下列图形中,对称轴条数最多的是( )A、等边三角形 B、矩形 C、正方形 D、圆6. 如图,在矩形纸片中, , , 将沿折叠到位置,交于点 , 则的值为( )
5. 下列图形中,对称轴条数最多的是( )A、等边三角形 B、矩形 C、正方形 D、圆6. 如图,在矩形纸片中, , , 将沿折叠到位置,交于点 , 则的值为( )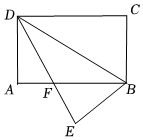 A、 B、 C、 D、7. 2022年4月16日,神舟十三号载人飞船圆满完成全部既定任务,顺利返回地球家园.六个月的飞天之旅展现了中国航天科技的新高度下列航天图标,其文字上方的图案是中心对称图形的是( )A、
A、 B、 C、 D、7. 2022年4月16日,神舟十三号载人飞船圆满完成全部既定任务,顺利返回地球家园.六个月的飞天之旅展现了中国航天科技的新高度下列航天图标,其文字上方的图案是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 8. 下列四种图形中,对称轴条数最多的是( )A、等边三角形 B、圆 C、长方形 D、正方形9. 现实世界中,对称现象无处不在,中国的方块字中有些也具有对称性.下列汉字是轴对称图形的是( )A、
8. 下列四种图形中,对称轴条数最多的是( )A、等边三角形 B、圆 C、长方形 D、正方形9. 现实世界中,对称现象无处不在,中国的方块字中有些也具有对称性.下列汉字是轴对称图形的是( )A、 B、
B、 C、
C、 D、
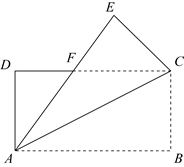
D、 10. 下列英文字母为轴对称图形的是( )A、W B、L C、S D、Q11. 平面直角坐标系中,点P(2,1)关于x轴对称的点的坐标是( )A、 B、 C、 D、12. 如图是战机在空中展示的轴对称队形.以飞机 B、C所在直线为x轴、队形的对称轴为y轴,建立平面直角坐标系.若飞机E的坐标为(40,a),则飞机D的坐标为( )
10. 下列英文字母为轴对称图形的是( )A、W B、L C、S D、Q11. 平面直角坐标系中,点P(2,1)关于x轴对称的点的坐标是( )A、 B、 C、 D、12. 如图是战机在空中展示的轴对称队形.以飞机 B、C所在直线为x轴、队形的对称轴为y轴,建立平面直角坐标系.若飞机E的坐标为(40,a),则飞机D的坐标为( ) A、 B、 C、 D、13. 下列选项中的垃圾分类图标,既是中心对称图形,又是轴对称图形的是( )
A、 B、 C、 D、13. 下列选项中的垃圾分类图标,既是中心对称图形,又是轴对称图形的是( )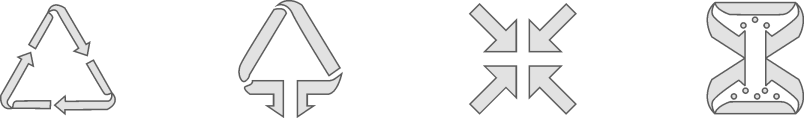 A、可回收物 B、其他垃圾 C、有害垃圾 D、厨余垃圾14. 如图, , 点M、N分别在边上,且 , 点P、Q分别在边上,则的最小值是( )
A、可回收物 B、其他垃圾 C、有害垃圾 D、厨余垃圾14. 如图, , 点M、N分别在边上,且 , 点P、Q分别在边上,则的最小值是( ) A、 B、 C、 D、15. 如图,已知BD是矩形ABCD的对角线,AB=6,BC=8,点E,F分别在边AD,BC上,连结BE,DF.将△ABE沿BE翻折,将△DCF沿DF翻折,若翻折后,点A,C分别落在对角线BD上的点G,H处,连结GF.则下列结论不正确的是( )
A、 B、 C、 D、15. 如图,已知BD是矩形ABCD的对角线,AB=6,BC=8,点E,F分别在边AD,BC上,连结BE,DF.将△ABE沿BE翻折,将△DCF沿DF翻折,若翻折后,点A,C分别落在对角线BD上的点G,H处,连结GF.则下列结论不正确的是( ) A、BD=10 B、HG=2 C、EG∥FH D、GF⊥BC
A、BD=10 B、HG=2 C、EG∥FH D、GF⊥BC二、填空题
-
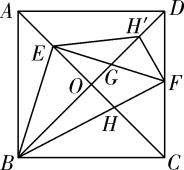
16. 如图,在正方形ABCD中, ,对角线 相交于点O.点E是对角线AC上一点,连接BE,过点E作 ,分别交 于点F、G,连接BF,交AC于点H,将 沿EF翻折,点H的对应点 恰好落在BD上,得到 若点F为CD的中点,则 的周长是.
 17. 如图,折叠边长为4cm的正方形纸片 , 折痕是 , 点落在点处,分别延长、交于点、 , 若点是边的中点,则cm.
17. 如图,折叠边长为4cm的正方形纸片 , 折痕是 , 点落在点处,分别延长、交于点、 , 若点是边的中点,则cm. 18. 如图,在矩形ABCD中 .动点M从点A出发,沿边AD向点D匀速运动,动点N从点B出发,沿边BC向点C匀速运动,连接MN.动点M,N同时出发,点M运动的速度为 ,点N运动的速度为 ,且 .当点N到达点C时,M,N两点同时停止运动.在运动过程中,将四边形MABN沿MN翻折,得到四边形 .若在某一时刻,点B的对应点 恰好在CD的中点重合,则 的值为.
18. 如图,在矩形ABCD中 .动点M从点A出发,沿边AD向点D匀速运动,动点N从点B出发,沿边BC向点C匀速运动,连接MN.动点M,N同时出发,点M运动的速度为 ,点N运动的速度为 ,且 .当点N到达点C时,M,N两点同时停止运动.在运动过程中,将四边形MABN沿MN翻折,得到四边形 .若在某一时刻,点B的对应点 恰好在CD的中点重合,则 的值为.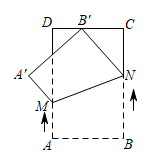 19. 如图,一束光沿CD方向,先后经过平面镜OB、OA反射后,沿EF方向射出,已知∠AOB=120°,∠CDB=20°,则∠AEF=
19. 如图,一束光沿CD方向,先后经过平面镜OB、OA反射后,沿EF方向射出,已知∠AOB=120°,∠CDB=20°,则∠AEF=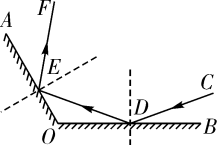 20. 如图,将⊙O沿弦AB折叠,恰经过圆心O,若AB=2 , 则阴影部分的面积为 .
20. 如图,将⊙O沿弦AB折叠,恰经过圆心O,若AB=2 , 则阴影部分的面积为 .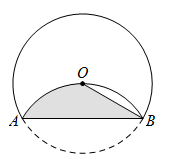
三、解答题
-
21. 根据以下素材,探索完成任务.
如何设计拱桥景观灯的悬挂方案?
素材1
图1中有一座拱桥,图2是其抛物线形桥拱的示意图,某时测得水面宽 20m ,拱顶离水面 5m .据调查,该河段水位在此基础上再涨 1.8m 达到最高.
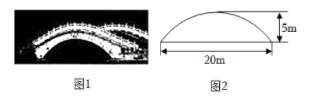
素材2
为迎佳节,拟在图1桥洞前面的桥拱上悬挂 40cm 长的灯笼,如图3.为了安全,灯笼底部距离水面不小于 1m ;为了实效,相邻两盏灯笼悬挂点的水平间距均为 1.6m ;为了美观,要求在符合条件处都挂上灯笼,且挂满后成轴对称分布.
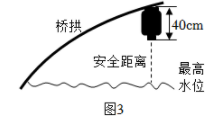
问题解决
任务1
确定桥拱形状
在图2中建立合适的直角坐标系,求抛物线的函数表达式.
任务2
探究悬挂范围
在你所建立的坐标系中,仅在安全的条件下,确定悬挂点的纵坐标的最小值和横坐标的取值范围.
任务3
拟定设计方案
给出一种符合所有悬挂条件的灯笼数量,并根据你所建立的坐标系,求出最左边一盏灯笼悬挂点的横坐标.
四、综合题
-
22. 如图1,矩形中, , 点P在边上,且不与点B、C重合,直线与的延长线交于点E.

 (1)、当点P是的中点时,求证:;(2)、将沿直线折叠得到 , 点落在矩形的内部,延长交直线于点F.
(1)、当点P是的中点时,求证:;(2)、将沿直线折叠得到 , 点落在矩形的内部,延长交直线于点F.①证明 , 并求出在(1)条件下的值;
②连接 , 求周长的最小值;
③如图2,交于点H,点G是的中点,当时,请判断与的数量关系,并说明理由.
23. 在平面直角坐标系中,已知一次函数与坐标轴分别交于 , 两点,且与反比例函数的图象在第一象限内交于P,K两点,连接 , 的面积为 .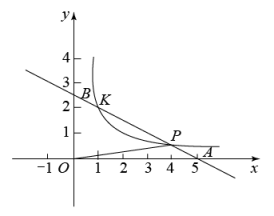 (1)、求一次函数与反比例函数的解析式;(2)、当时,求x的取值范围;(3)、若C为线段上的一个动点,当最小时,求的面积.
(1)、求一次函数与反比例函数的解析式;(2)、当时,求x的取值范围;(3)、若C为线段上的一个动点,当最小时,求的面积.
-