2022年中考数学真题分类汇编:18 四边形
试卷更新日期:2022-07-12 类型:二轮复习
一、单选题
-
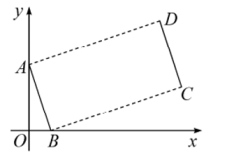
1. 如图,点 , 将线段平移得到线段 , 若 , 则点D的坐标是( )
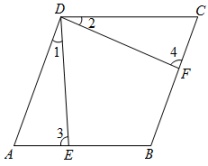
 A、 B、 C、 D、2. 如图,菱形中,点E是边的中点,垂直交的延长线于点F,若 , 则菱形的边长是( )
A、 B、 C、 D、2. 如图,菱形中,点E是边的中点,垂直交的延长线于点F,若 , 则菱形的边长是( )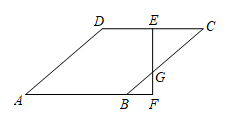 A、3 B、4 C、5 D、3. 如图,在边长为2的等边三角形的外侧作正方形 , 过点作 , 垂足为 , 则的长为( )
A、3 B、4 C、5 D、3. 如图,在边长为2的等边三角形的外侧作正方形 , 过点作 , 垂足为 , 则的长为( ) A、 B、 C、 D、4. 一块直角三角板按如图所示方式放置在一张长方形纸条上,若 , 则的度数为( )
A、 B、 C、 D、4. 一块直角三角板按如图所示方式放置在一张长方形纸条上,若 , 则的度数为( )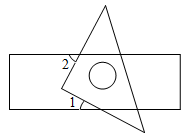 A、28° B、56° C、36° D、62°5. 如图,定直线MNPQ,点B、C分别为MN、PQ上的动点,且BC=12,BC在两直线间运动过程中始终有∠BCQ=60°.点A是MN上方一定点,点D是PQ下方一定点,且AEBCDF,AE=4,DF=8,AD=24 , 当线段BC在平移过程中,AB+CD的最小值为( )
A、28° B、56° C、36° D、62°5. 如图,定直线MNPQ,点B、C分别为MN、PQ上的动点,且BC=12,BC在两直线间运动过程中始终有∠BCQ=60°.点A是MN上方一定点,点D是PQ下方一定点,且AEBCDF,AE=4,DF=8,AD=24 , 当线段BC在平移过程中,AB+CD的最小值为( )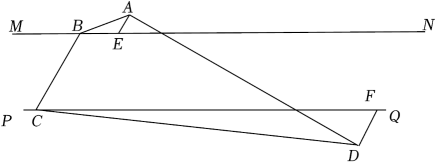 A、24 B、24 C、12 D、126. 如图,正方形ABCD的对角线AC,BD相交于点O,点F是CD上一点,交BC于点E,连接AE,BF交于点P,连接OP.则下列结论:①;②;③;④若 , 则;⑤四边形OECF的面积是正方形ABCD面积的 . 其中正确的结论是( )
A、24 B、24 C、12 D、126. 如图,正方形ABCD的对角线AC,BD相交于点O,点F是CD上一点,交BC于点E,连接AE,BF交于点P,连接OP.则下列结论:①;②;③;④若 , 则;⑤四边形OECF的面积是正方形ABCD面积的 . 其中正确的结论是( ) A、①②④⑤ B、①②③⑤ C、①②③④ D、①③④⑤7. 如图,在矩形中,P是边上的一个动点,连接 , , 过点B作射线,交线段的延长线于点E,交边于点M,且使得 , 如果 , , , , 其中 . 则下列结论中,正确的个数为( )
A、①②④⑤ B、①②③⑤ C、①②③④ D、①③④⑤7. 如图,在矩形中,P是边上的一个动点,连接 , , 过点B作射线,交线段的延长线于点E,交边于点M,且使得 , 如果 , , , , 其中 . 则下列结论中,正确的个数为( )⑴y与x的关系式为;(2)当时,;(3)当时, .
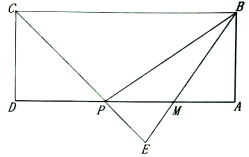 A、0个 B、1个 C、2个 D、3个8. 如图,在 中,一定正确的是( )
A、0个 B、1个 C、2个 D、3个8. 如图,在 中,一定正确的是( ) A、 B、 C、 D、9. 如图,在矩形纸片中, , , 将沿折叠到位置,交于点 , 则的值为( )
A、 B、 C、 D、9. 如图,在矩形纸片中, , , 将沿折叠到位置,交于点 , 则的值为( ) A、 B、 C、 D、10. 如图,在矩形中, , 连接 , 分别以点 , 为圆心,大于的长为半径画弧,两弧交于点 , , 直线分别交 , 于点 , 下列结论:
A、 B、 C、 D、10. 如图,在矩形中, , 连接 , 分别以点 , 为圆心,大于的长为半径画弧,两弧交于点 , , 直线分别交 , 于点 , 下列结论:四边形是菱形;;;若平分 , 则.
其中正确结论的个数是( )
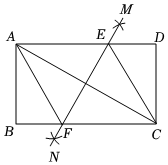 A、4 B、3 C、2 D、111. 依据所标数据,下列一定为平行四边形的是()A、
A、4 B、3 C、2 D、111. 依据所标数据,下列一定为平行四边形的是()A、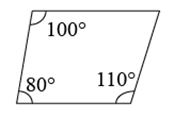 B、
B、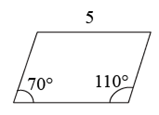 C、
C、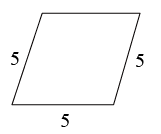 D、
D、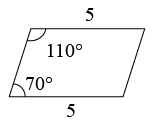 12. 中国古代数学家赵爽在为《周髀算经》作注解时,用4个全等的直角三角形拼成正方形(如图),并用它证明了勾股定理,这个图被称为“弦图”,若“弦图”中小正方形面积与每个直角三角形面积均为1,α为直角三角形中的一个锐角,则tanα=( )
12. 中国古代数学家赵爽在为《周髀算经》作注解时,用4个全等的直角三角形拼成正方形(如图),并用它证明了勾股定理,这个图被称为“弦图”,若“弦图”中小正方形面积与每个直角三角形面积均为1,α为直角三角形中的一个锐角,则tanα=( )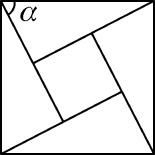 A、2 B、 C、 D、13. 在▱ABCD中(如图),连接AC,已知∠BAC=40°,∠ACB=80°,则∠BCD=( )
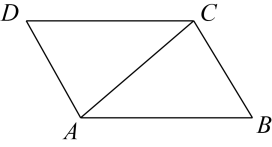
A、2 B、 C、 D、13. 在▱ABCD中(如图),连接AC,已知∠BAC=40°,∠ACB=80°,则∠BCD=( )
 A、80° B、100° C、120° D、140°14. 七巧板是一种古老的中国传统智力玩具,如图,在正方形纸板ABCD中,BD为对角线,E,F分别为BC,CD的中点,分别交BD,EF于O,P两点,M,N分别为BO,DC的中点,连接AP,NF,沿图中实线剪开即可得到一副七巧板,则在剪开之前,关于该图形,下列说法:①图中的三角形都是等腰直角三角形;②四边形MPEB是菱形;③四边形PFDM的面积占正方形ABCD面积的.正确的有( )
A、80° B、100° C、120° D、140°14. 七巧板是一种古老的中国传统智力玩具,如图,在正方形纸板ABCD中,BD为对角线,E,F分别为BC,CD的中点,分别交BD,EF于O,P两点,M,N分别为BO,DC的中点,连接AP,NF,沿图中实线剪开即可得到一副七巧板,则在剪开之前,关于该图形,下列说法:①图中的三角形都是等腰直角三角形;②四边形MPEB是菱形;③四边形PFDM的面积占正方形ABCD面积的.正确的有( )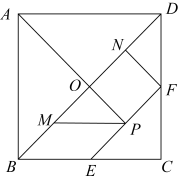 A、只有① B、①② C、①③ D、②③15. 在下列条件中,能够判定为矩形的是( )A、 B、 C、 D、
A、只有① B、①② C、①③ D、②③15. 在下列条件中,能够判定为矩形的是( )A、 B、 C、 D、二、填空题
-
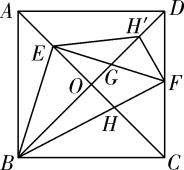
16. 如图,在正方形ABCD中, ,对角线 相交于点O.点E是对角线AC上一点,连接BE,过点E作 ,分别交 于点F、G,连接BF,交AC于点H,将 沿EF翻折,点H的对应点 恰好落在BD上,得到 若点F为CD的中点,则 的周长是.
 17. 如图,正方形中,点E、F分别在边上, , 则;若的面积等于1,则的值是.
17. 如图,正方形中,点E、F分别在边上, , 则;若的面积等于1,则的值是.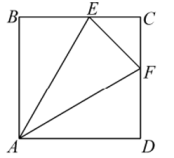 18. 如图,矩形的对角线 , 相交于点 , // , //.若 , 则四边形的周长是.
18. 如图,矩形的对角线 , 相交于点 , // , //.若 , 则四边形的周长是. 19. 如图,折叠边长为4cm的正方形纸片 , 折痕是 , 点落在点处,分别延长、交于点、 , 若点是边的中点,则cm.
19. 如图,折叠边长为4cm的正方形纸片 , 折痕是 , 点落在点处,分别延长、交于点、 , 若点是边的中点,则cm. 20. 如图,在四边形ABCD中,AC⊥BD,垂足为O, , 要使四边形ABCD为菱形,应添加的条件是 . (只需写出一个条件即可)
20. 如图,在四边形ABCD中,AC⊥BD,垂足为O, , 要使四边形ABCD为菱形,应添加的条件是 . (只需写出一个条件即可)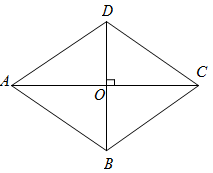
三、解答题
-
21. 如图,在菱形中,对角线 , 相交于点 , 点 , 在对角线上,且 , .
求证:四边形是正方形.
 22. 小惠自编一题:“如图,在四边形ABCD中,对角线AC,BD交于点O,AC⊥BD,OB=OD.求证:四边形ABCD是菱形”,并将自己的证明过程与同学小洁交流.
22. 小惠自编一题:“如图,在四边形ABCD中,对角线AC,BD交于点O,AC⊥BD,OB=OD.求证:四边形ABCD是菱形”,并将自己的证明过程与同学小洁交流.
小惠:
证明:∵AC⊥BD,OB=OD,
∴AC垂直平分BD.
∴AB=AD,CB=CD,
∴四边形ABCD是菱形.
小洁:
这个题目还缺少条件,需要补充一个条件才能证明.
若赞同小惠的证法,请在第一个方框内打“√”;若赞成小洁的说法,请你补充一个条件,并证明.
四、综合题
-
23. 如图,在 中,BD是它的一条对角线,
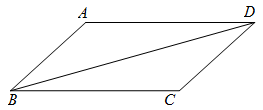 (1)、求证: ;(2)、尺规作图:作BD的垂直平分线EF,分别交AD,BC于点E,F(不写作法,保留作图痕迹);(3)、连接BE,若 ,求 的度数.24. 如图,在中,对角线AC,BD相交于点O,.
(1)、求证: ;(2)、尺规作图:作BD的垂直平分线EF,分别交AD,BC于点E,F(不写作法,保留作图痕迹);(3)、连接BE,若 ,求 的度数.24. 如图,在中,对角线AC,BD相交于点O,. (1)、求证:;(2)、若点E,F分别为AD,AO的中点,连接EF, , 求BD的长及四边形ABCD的周长.
(1)、求证:;(2)、若点E,F分别为AD,AO的中点,连接EF, , 求BD的长及四边形ABCD的周长.