2022年中考数学真题分类汇编:14 二次函数
试卷更新日期:2022-07-12 类型:二轮复习
一、单选题
-
1. 已知二次函数(为常数,),点是该函数图象上一点,当时, , 则的取值范围是( )A、或 B、 C、或 D、2. 如图,已知二次函数y=ax2+bx+c(a、b、c为常数,且a≠0)的图象顶点为P(1,m),经过点A(2,1);有以下结论:①a<0;②abc>0;③4a+2b+c=1;④x>1时,y随x的增大而减小;⑤对于任意实数t,总有at2+bt≤a+b,其中正确的有( )
 A、2个 B、3个 C、4个 D、5个3. 若二次函数的图象如图所示,则一次函数与反比例函数在同一坐标系内的大致图象为( )
A、2个 B、3个 C、4个 D、5个3. 若二次函数的图象如图所示,则一次函数与反比例函数在同一坐标系内的大致图象为( ) A、
A、 B、
B、 C、
C、 D、
D、 4. 已知二次函数的部分函数图象如图所示,则一次函数与反比例函数在同一平面直角坐标系中的图象大致是( )
4. 已知二次函数的部分函数图象如图所示,则一次函数与反比例函数在同一平面直角坐标系中的图象大致是( ) A、
A、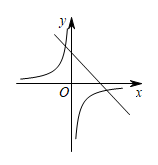 B、
B、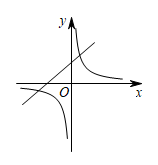 C、
C、 D、
D、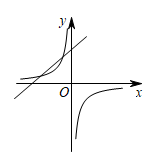 5. 如图,二次函数的图象与y轴的交点在(0,1)与(0,2)之间,对称轴为 , 函数最大值为4,结合图象给出下列结论:①;②;③;④若关于x的一元二次方程 有两个不相等的实数根,则m>4;⑤当x<0时,y随x的增大而减小.其中正确的结论有( )
5. 如图,二次函数的图象与y轴的交点在(0,1)与(0,2)之间,对称轴为 , 函数最大值为4,结合图象给出下列结论:①;②;③;④若关于x的一元二次方程 有两个不相等的实数根,则m>4;⑤当x<0时,y随x的增大而减小.其中正确的结论有( )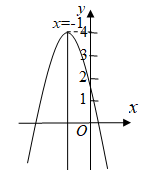 A、2个 B、3个 C、4个 D、5个6. 如图,二次函数y=ax2+bx(a≠0)的图像过点(2,0),下列结论错误的是( )
A、2个 B、3个 C、4个 D、5个6. 如图,二次函数y=ax2+bx(a≠0)的图像过点(2,0),下列结论错误的是( )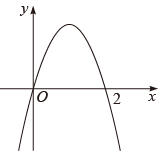 A、b>0 B、a+b>0 C、x=2是关于x的方程ax2+bx=0(a≠0)的一个根 D、点(x1 , y1),(x2 , y2)在二次函数的图象上,当x1>x2>2时,y2<y1<07. 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)abc<0;(2)4a+c>2b;(3)3b﹣2c>0;(4)若点A(﹣2,y1)、点B(﹣ , y2)、点C( , y3)在该函数图象上,则y1<y3<y2;(5)4a+2b≥m(am+b)(m为常数).其中正确的结论有( )
A、b>0 B、a+b>0 C、x=2是关于x的方程ax2+bx=0(a≠0)的一个根 D、点(x1 , y1),(x2 , y2)在二次函数的图象上,当x1>x2>2时,y2<y1<07. 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)abc<0;(2)4a+c>2b;(3)3b﹣2c>0;(4)若点A(﹣2,y1)、点B(﹣ , y2)、点C( , y3)在该函数图象上,则y1<y3<y2;(5)4a+2b≥m(am+b)(m为常数).其中正确的结论有( )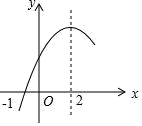 A、5个 B、4个 C、3个 D、2个8. 已知抛物线(a,b,c是常数,)经过点 , 有下列结论:
A、5个 B、4个 C、3个 D、2个8. 已知抛物线(a,b,c是常数,)经过点 , 有下列结论:①;
②当时,y随x的增大而增大;
③关于x的方程有两个不相等的实数根.
其中,正确结论的个数是( )
A、0 B、1 C、2 D、39. 已知二次函数 , 其中、 , 则该函数的图象可能为( )A、 B、
B、 C、
C、 D、
D、 10. 已知二次函数y=x2−2x−3的自变量x1 , x2 , x3对应的函数值分别为y1 , y2 , y3.当−1<x1<0,1<x2<2,x3>3时,y1 , y2 , y3三者之间的大小关系是( )A、 B、 C、 D、11. 已知点A(a,b),B(4,c)在直线y=kx+3(k为常数,k≠0)上,若ab的最大值为9,则c的值为( )A、1 B、 C、2 D、12. 已知抛物线 , 下列结论错误的是( )A、抛物线开口向上 B、抛物线的对称轴为直线 C、抛物线的顶点坐标为 D、当时,y随x的增大而增大13. 在同一平面直角坐标系中,一次函数与的图像可能是( )A、
10. 已知二次函数y=x2−2x−3的自变量x1 , x2 , x3对应的函数值分别为y1 , y2 , y3.当−1<x1<0,1<x2<2,x3>3时,y1 , y2 , y3三者之间的大小关系是( )A、 B、 C、 D、11. 已知点A(a,b),B(4,c)在直线y=kx+3(k为常数,k≠0)上,若ab的最大值为9,则c的值为( )A、1 B、 C、2 D、12. 已知抛物线 , 下列结论错误的是( )A、抛物线开口向上 B、抛物线的对称轴为直线 C、抛物线的顶点坐标为 D、当时,y随x的增大而增大13. 在同一平面直角坐标系中,一次函数与的图像可能是( )A、 B、
B、 C、
C、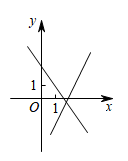 D、
D、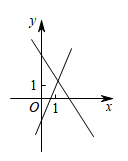 14. 如图,抛物线与x轴相交于点 , 与y轴相交于点C,小红同学得出了以下结论:①;②;③当时,;④ . 其中正确的个数为( )
14. 如图,抛物线与x轴相交于点 , 与y轴相交于点C,小红同学得出了以下结论:①;②;③当时,;④ . 其中正确的个数为( )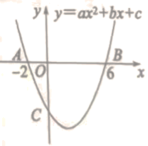 A、4 B、3 C、2 D、115. 点A (m-1,y1),B(m,y2)都在二次函数y=(x-1)2+n的图象上。若y1<y2 , 则m的取值范围为( )A、m>2 B、m> C、m<1 D、 <m<2
A、4 B、3 C、2 D、115. 点A (m-1,y1),B(m,y2)都在二次函数y=(x-1)2+n的图象上。若y1<y2 , 则m的取值范围为( )A、m>2 B、m> C、m<1 D、 <m<2二、填空题
-
16. 在平面直角坐标系中,将抛物线先绕原点旋转180°,再向下平移5个单位,所得到的抛物线的顶点坐标是.17. 已知抛物线( , , 是常数)开口向下,过 , 两点,且.下列四个结论:
①;
②若 , 则;
③若点 , 在抛物线上, , 且 , 则;
④当时,关于的一元二次方程必有两个不相等的实数根.
其中正确的是(填写序号).
18. 如图,用一段长为的篱芭围成一个一边靠墙的矩形围栏(墙足够长),则这个围栏的最大面积为.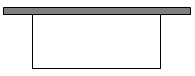 19. 如图,以一定的速度将小球沿与地面成一定角度的方向击出时,小球的飞行路线是一条抛物线.若不考虑空气阻力,小球的飞行高度 (单位:m)与飞行时间 (单位:s)之间具有函数关系: ,则当小球飞行高度达到最高时,飞行时间 s.
19. 如图,以一定的速度将小球沿与地面成一定角度的方向击出时,小球的飞行路线是一条抛物线.若不考虑空气阻力,小球的飞行高度 (单位:m)与飞行时间 (单位:s)之间具有函数关系: ,则当小球飞行高度达到最高时,飞行时间 s. 20. 抛物线y=ax2+bx+c(a,b,c为常数)的部分图象如图所示,设m=a﹣b+c,则m的取值范围是 .
20. 抛物线y=ax2+bx+c(a,b,c为常数)的部分图象如图所示,设m=a﹣b+c,则m的取值范围是 .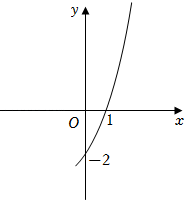
三、解答题
-
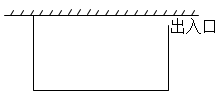
21. 某农场要建一个矩形养鸡场,鸡场的一边靠墙,另外三边用木栅栏围成.已知墙长25m,木栅栏长47m,在与墙垂直的一边留出1m宽的出入口(另选材料建出入门).求鸡场面积的最大值.
 22. 根据以下素材,探索完成任务.
22. 根据以下素材,探索完成任务.如何设计拱桥景观灯的悬挂方案?
素材1
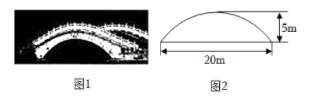
图1中有一座拱桥,图2是其抛物线形桥拱的示意图,某时测得水面宽 20m ,拱顶离水面 5m .据调查,该河段水位在此基础上再涨 1.8m 达到最高.
素材2
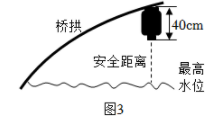
为迎佳节,拟在图1桥洞前面的桥拱上悬挂 40cm 长的灯笼,如图3.为了安全,灯笼底部距离水面不小于 1m ;为了实效,相邻两盏灯笼悬挂点的水平间距均为 1.6m ;为了美观,要求在符合条件处都挂上灯笼,且挂满后成轴对称分布.
问题解决
任务1
确定桥拱形状
在图2中建立合适的直角坐标系,求抛物线的函数表达式.
任务2
探究悬挂范围
在你所建立的坐标系中,仅在安全的条件下,确定悬挂点的纵坐标的最小值和横坐标的取值范围.
任务3
拟定设计方案
给出一种符合所有悬挂条件的灯笼数量,并根据你所建立的坐标系,求出最左边一盏灯笼悬挂点的横坐标.
四、综合题
-
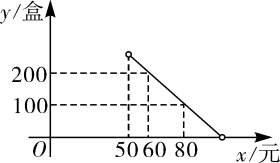
23. 打油茶是广西少数民族特有的一种民俗,某特产公司近期销售一种盒装油茶,每盒的成本价为50元,经市场调研发现,该种油茶的月销售量y(盒)与销售单价x(元)之间的函数图象如图所示.
 (1)、求y与x的函数解析式,并写出自变量x的取值范围;(2)、当销售单价定为多少元时,该种油茶的月销售利润最大?求出最大利润.24. 如图,抛物线的对称轴是直线 , 与轴交于点 , , 与轴交于点 , 连接.
(1)、求y与x的函数解析式,并写出自变量x的取值范围;(2)、当销售单价定为多少元时,该种油茶的月销售利润最大?求出最大利润.24. 如图,抛物线的对称轴是直线 , 与轴交于点 , , 与轴交于点 , 连接. (1)、求此抛物线的解析式;(2)、已知点是第一象限内抛物线上的一个动点,过点作轴,垂足为点 , 交直线于点 , 是否存在这样的点 , 使得以 , , 为顶点的三角形是等腰三角形.若存在,请求出点的坐标,若不存在,请说明理由;(3)、已知点是抛物线对称轴上的点,在坐标平面内是否存在点 , 使以点、、、为顶点的四边形为矩形,若存在,请直接写出点的坐标;若不存在,请说明理由.25. 如图,在平面直角坐标系中,抛物线与x轴交于A,B两点,与y轴交于点C,顶点为 , 抛物线的对称轴交直线于点E.
(1)、求此抛物线的解析式;(2)、已知点是第一象限内抛物线上的一个动点,过点作轴,垂足为点 , 交直线于点 , 是否存在这样的点 , 使得以 , , 为顶点的三角形是等腰三角形.若存在,请求出点的坐标,若不存在,请说明理由;(3)、已知点是抛物线对称轴上的点,在坐标平面内是否存在点 , 使以点、、、为顶点的四边形为矩形,若存在,请直接写出点的坐标;若不存在,请说明理由.25. 如图,在平面直角坐标系中,抛物线与x轴交于A,B两点,与y轴交于点C,顶点为 , 抛物线的对称轴交直线于点E. (1)、求抛物线的表达式;(2)、把上述抛物线沿它的对称轴向下平移,平移的距离为 , 在平移过程中,该抛物线与直线始终有交点,求h的最大值;(3)、M是(1)中抛物线上一点,N是直线上一点.是否存在以点D,E,M,N为顶点的四边形是平行四边形?若存在,求出点N的坐标;若不存在,请说明理由.
(1)、求抛物线的表达式;(2)、把上述抛物线沿它的对称轴向下平移,平移的距离为 , 在平移过程中,该抛物线与直线始终有交点,求h的最大值;(3)、M是(1)中抛物线上一点,N是直线上一点.是否存在以点D,E,M,N为顶点的四边形是平行四边形?若存在,求出点N的坐标;若不存在,请说明理由.