浙江省杭州市上城区2021-2022学年七年级下学期期末数学试卷
试卷更新日期:2022-07-12 类型:期末考试
一、单选题
-
1. 某细胞的直径约为0.000123毫米,将0.000123用科学记数法表示为( )A、 B、 C、 D、2. 下列各式是二元一次方程的是( )A、 B、 C、 D、3. 下列运算正确的是( )A、 B、 C、 D、4. 在下列从左到右的变形中,不是因式分解的是( )A、 B、 C、 D、5. 如图是甲、乙两公司2021年1-8月份的盈利情况图,根据图中提供的信息,下列说法错误的是( )
 A、两公司在8月份的利润相同 B、甲公司的利润逐月递减 C、甲公司的利润有4个月高于乙公司的利润 D、乙公司4月份的利润最高6. 如图,将直角 沿边 的方向平移到 的位置,连接 ,若 ,则 的长为( )
A、两公司在8月份的利润相同 B、甲公司的利润逐月递减 C、甲公司的利润有4个月高于乙公司的利润 D、乙公司4月份的利润最高6. 如图,将直角 沿边 的方向平移到 的位置,连接 ,若 ,则 的长为( )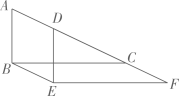 A、3 B、4 C、5 D、67. 不论x取何值,下列代数式的值不可能为0的是( )A、 B、 C、 D、8. 已知x,y满足方程组 ,则无论m取何值,x、y恒有关系式是( )A、 B、 C、 D、9. 原来花100元能购买某种糖果m千克,由于成本上涨,糖果涨价10%,那么涨价后花100元能买到糖果( ) 千克A、 B、 C、 D、10. 如图, AB∥CD,AD∥BC,AD⊥CD,点E为线段BC上一点,将线段AB沿AE折叠,点B的对应点F落在四边形ABCD外侧,连接EF,若AF∥BD , ,则 为( )
A、3 B、4 C、5 D、67. 不论x取何值,下列代数式的值不可能为0的是( )A、 B、 C、 D、8. 已知x,y满足方程组 ,则无论m取何值,x、y恒有关系式是( )A、 B、 C、 D、9. 原来花100元能购买某种糖果m千克,由于成本上涨,糖果涨价10%,那么涨价后花100元能买到糖果( ) 千克A、 B、 C、 D、10. 如图, AB∥CD,AD∥BC,AD⊥CD,点E为线段BC上一点,将线段AB沿AE折叠,点B的对应点F落在四边形ABCD外侧,连接EF,若AF∥BD , ,则 为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 因式分解: .
12. 请写出一个解为 的二元一次方程:.13. 某中学共40位同学参加了演讲比赛,分段统计参赛同学的成绩,结果如下(分数为整数,满分为100分)分数段(分〕
61~70
71~80
81~90
91~100
人数
5
10
16
则m=;若制作成扇形统计图,那么81~90分数段所对应扇形的圆心角为°.
14. 如图, , ,当 °时, .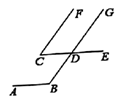 15. 若代数式 可以表示为 的形式,则a=.16. , , 等代数式,如果交换m和n的位置,式子的值不变,我们把这样的式子叫做完美对称式. 若关于x,y的分式 是完美对称式,则: ;若完美对称式 满足: ,且 ,则 (用含x的代数式表示).
15. 若代数式 可以表示为 的形式,则a=.16. , , 等代数式,如果交换m和n的位置,式子的值不变,我们把这样的式子叫做完美对称式. 若关于x,y的分式 是完美对称式,则: ;若完美对称式 满足: ,且 ,则 (用含x的代数式表示).三、解答题
-
17. 计算或化简:(1)、 ;(2)、 .18. 解方程(组):(1)、(2)、19. 老师设计了接力游戏,用合作的方式完成分式化简,规则是:每人只能看到前一人给的式子,并进行一步计算,再将结果传递给下一人,最后完成化简. 过程如图所示:
 (1)、接力中,自己负责的一步出现错误的同学是;(2)、请你书写正确的化简过程,并在“-1,0,1”中选择一个合适的数代入求值.20. 为了更好地宣传垃圾分类,某校组织开展垃圾分类知识竞赛,并随机抽查了部分参赛同学的成绩,整理并制作了不完整的统计表和统计图,请根据图表中提供的信息解答问题:
(1)、接力中,自己负责的一步出现错误的同学是;(2)、请你书写正确的化简过程,并在“-1,0,1”中选择一个合适的数代入求值.20. 为了更好地宣传垃圾分类,某校组织开展垃圾分类知识竞赛,并随机抽查了部分参赛同学的成绩,整理并制作了不完整的统计表和统计图,请根据图表中提供的信息解答问题:分数 (分)
频数
频率
30
0.1
90
0.4
60
0.2
 (1)、本次调查统计的学生人数为;(2)、n= , 并补全频数分布直方图;(3)、该校有学生1500人,成绩在80分以上(含80分)的为优秀,假如全部学生参加此次测试,请估计该校学生成绩为优秀的人数.21. 如图,已知 , .
(1)、本次调查统计的学生人数为;(2)、n= , 并补全频数分布直方图;(3)、该校有学生1500人,成绩在80分以上(含80分)的为优秀,假如全部学生参加此次测试,请估计该校学生成绩为优秀的人数.21. 如图,已知 , . (1)、证明: ;(2)、若 , ,求 的度数.22. 如图,点D在长方形 的边 上,且四边形 、四边形 均为正方形,延长 交 于点M,设 , , 的面积记为 ,四边形 的面积记为 ,长方形 的面积记为 .
(1)、证明: ;(2)、若 , ,求 的度数.22. 如图,点D在长方形 的边 上,且四边形 、四边形 均为正方形,延长 交 于点M,设 , , 的面积记为 ,四边形 的面积记为 ,长方形 的面积记为 .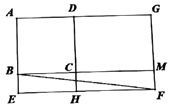 (1)、用a、b的代数式表示 和 ;(2)、若 ,求 的值;(3)、若 ,求 的长.23. 某体育用品商场销售A、B两款足球,售价和进价如下表:
(1)、用a、b的代数式表示 和 ;(2)、若 ,求 的值;(3)、若 ,求 的长.23. 某体育用品商场销售A、B两款足球,售价和进价如下表:类型
进价(元/个)
售价(元/个)
A款
m
120
B款
n
90
若该商场购进10个A款足球和20个B款足球需2000元;若该商场购进20个A款足球和30个B款足球需3400元.
(1)、求m和n的值;(2)、某校在该商场一次性购买A款足球x个和B款足球y个,共消费3600元,那么该商场可获利多少元?(3)、为了提高销量,商场实施:“买足球送跳绳”的促销活动:“买1个A款足球送1根跳绳,买3个B款足球送2根跳绳”,每根跳绳的成本为10元,某日售卖两款足球总计盈利600元,那么该日销售A、B两款足球各多少个?