浙江省宁波市镇海区2021-2022学年八年级下学期期末数学试卷
试卷更新日期:2022-07-12 类型:期末考试
一、单选题
-
1. 2022年北京冬奥会会徽“冬梦”以汉字“冬”为灵感来源,将中国传统文化和奥林匹克元素巧妙结合.下面是历届奥运会会徽中的部分图形,其中既是轴对称图形,也是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 方程经配方后,可化为( )A、 B、 C、 D、3. 用反证法证明命题“三角形中至少有一个内角小于或等于60°”时,首先应该假设这个三角形中( )A、每一个内角都大于60° B、每一个内角都小于60° C、有一个内角大于60° D、有一个内角小于60°4. 如图,在四边形中, , 将沿翻折,得到.若 , 则的度数为( )
2. 方程经配方后,可化为( )A、 B、 C、 D、3. 用反证法证明命题“三角形中至少有一个内角小于或等于60°”时,首先应该假设这个三角形中( )A、每一个内角都大于60° B、每一个内角都小于60° C、有一个内角大于60° D、有一个内角小于60°4. 如图,在四边形中, , 将沿翻折,得到.若 , 则的度数为( )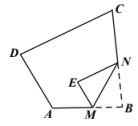 A、 B、 C、 D、5. 已知点 , , 都在反比例函数(m为常数)的图象上,那么的大小关系是( )A、 B、 C、 D、6. 将抛物线先向右平移1个单位长度,再向上平移2个单位长度,得到的抛物线的函数表达式为( )A、 B、 C、 D、7. 如图,一块长方形场地的长与宽的比为2∶1,于点E,于点F,连接 , 则四边形与长方形的面积比为( )
A、 B、 C、 D、5. 已知点 , , 都在反比例函数(m为常数)的图象上,那么的大小关系是( )A、 B、 C、 D、6. 将抛物线先向右平移1个单位长度,再向上平移2个单位长度,得到的抛物线的函数表达式为( )A、 B、 C、 D、7. 如图,一块长方形场地的长与宽的比为2∶1,于点E,于点F,连接 , 则四边形与长方形的面积比为( ) A、 B、 C、 D、8. 如图,菱形的四个顶点均在坐标轴上,对角线交于原点O,交于点G,反比例函数的图象经过线段的中点E,若 , 则的长为( )
A、 B、 C、 D、8. 如图,菱形的四个顶点均在坐标轴上,对角线交于原点O,交于点G,反比例函数的图象经过线段的中点E,若 , 则的长为( ) A、 B、 C、 D、9. 抛物线经过两点,若点 , 点也在抛物线上,且满足 , 则的大小关系为( )A、 B、 C、 D、无法确定10. 由四个全等的直角三角形和一个小正方形组成的大正方形如图所示.连接 , 设正方形的面积为 , 正方形的面积为 , 四边形的面积为.若 , 则下面结论一定正确的是( )
A、 B、 C、 D、9. 抛物线经过两点,若点 , 点也在抛物线上,且满足 , 则的大小关系为( )A、 B、 C、 D、无法确定10. 由四个全等的直角三角形和一个小正方形组成的大正方形如图所示.连接 , 设正方形的面积为 , 正方形的面积为 , 四边形的面积为.若 , 则下面结论一定正确的是( )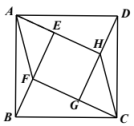 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 代数式有意义,则x的取值范围是.12. 一个多边形的内角和是它的外角和的4倍,则这个多边形的边数是 .13. 若菱形ABCD的两条对角线的长分别为一元二次方程x2-7x+12=0的实数根,则菱形ABCD的面积为14. 2021年6月17日,中国第7艘载人航天飞船“神舟十二号”圆满发射成功,激励更多的年轻人投身航天事业.现对学员们进行招飞前考核,其中某位学员心理素质、身体素质、科学头脑、应变能力四项测试得分分别为86分、85分、88分、90分,若按照心理素质、身体素质、科学头脑、应变能力的占比为4∶3∶2∶1的比例确定总分,则该名学员的总分为分.15. 如图,在平面直角坐标系中,的顶点C在x轴的正半轴上,点A是第一象限内一点,反比例函数的图象经过点A,与边交于点D,若与的面积相等,则的面积为.
 16. 如图1,中两条对角线交于点O, , 点P从顶点B出发,沿以每秒的速度匀速运动到点D,图2是点P运动过程中线段的长度y与时间t的函数关系图象,其中M、N分别是两段曲线的最低点,则点M的横坐标为 , 点N的纵坐标为.
16. 如图1,中两条对角线交于点O, , 点P从顶点B出发,沿以每秒的速度匀速运动到点D,图2是点P运动过程中线段的长度y与时间t的函数关系图象,其中M、N分别是两段曲线的最低点,则点M的横坐标为 , 点N的纵坐标为.
三、解答题
-
17. 计算:(1)、(2)、18. 如图是由边长为1的小正方形构成的的网格, 点均在格点上.
 (1)、在图1中画出以为对角线的正方形 , 点为格点.(2)、在图2中画出以为边且周长最大的平行四边形 , 点为格点 (画一个即可).19. 为了响应市“科学应对、群防群控、增强体质、战胜疫情”的号召,学校决定开展多项体育活动比赛,从八年级同学中任意选取40人,平均分成甲、乙两个小组进行“引体向上”体能测试,根据测试成绩绘制出如下的统计表和统计图(成绩均为整数,满分为10分).
(1)、在图1中画出以为对角线的正方形 , 点为格点.(2)、在图2中画出以为边且周长最大的平行四边形 , 点为格点 (画一个即可).19. 为了响应市“科学应对、群防群控、增强体质、战胜疫情”的号召,学校决定开展多项体育活动比赛,从八年级同学中任意选取40人,平均分成甲、乙两个小组进行“引体向上”体能测试,根据测试成绩绘制出如下的统计表和统计图(成绩均为整数,满分为10分).甲组成绩统计表:
成绩
7
8
9
10
人数
1
9
5
5
甲组成绩统计图:

请根据上面的信息,解答下列问题:
(1)、甲组成绩的众数是;(2)、m= , 乙组成绩的中位数是;(3)、已知甲组成绩的方差 , 求出乙组成绩的方差,并判断哪个小组的成绩更加稳定?20. 如图,一次函数y1=kx+b(k≠0)与反比例函数y2=(m≠0)的图象交于点A(1,2)和B(﹣2,a),与y轴交于点M. (1)、求一次函数和反比例函数的解析式;(2)、在y轴上取一点N,当△AMN的面积为3时,求点N的坐标;(3)、求不等式kx+b﹣<0的解集.(请直接写出答案)21. 如图1,在四边形中, , 对角线、交于点O,平分.
(1)、求一次函数和反比例函数的解析式;(2)、在y轴上取一点N,当△AMN的面积为3时,求点N的坐标;(3)、求不等式kx+b﹣<0的解集.(请直接写出答案)21. 如图1,在四边形中, , 对角线、交于点O,平分.
 (1)、求证:四边形是菱形;(2)、如图2,点E是边上一点,将四边形沿着翻折得到四边形 , 若点恰好落在边的中点处,且 , 求菱形的周长.22. “燃情冰雪,一起向未来”,北京冬奥会于2022年2月4日如约而至,某商家看准商机,进行冬奥会吉祥物“冰墩墩”纪念品的销售,每个纪念品进价40元.规定销售单价不低于44元,且不高于60元.销售期间发现,当销售单价定为44元时,每天可售出300个,由于销售火爆,商家决定提价销售.经市场调研发现,销售单价每上涨1元,每天销量减少10个.(1)、求当每个纪念品的销售单价是多少元时,商家每天获利2640元;(2)、将纪念品的销售单价定为多少元时,商家每天销售纪念品获得的利润w元最大?最大利润是多少元?23. 阅读理解:
(1)、求证:四边形是菱形;(2)、如图2,点E是边上一点,将四边形沿着翻折得到四边形 , 若点恰好落在边的中点处,且 , 求菱形的周长.22. “燃情冰雪,一起向未来”,北京冬奥会于2022年2月4日如约而至,某商家看准商机,进行冬奥会吉祥物“冰墩墩”纪念品的销售,每个纪念品进价40元.规定销售单价不低于44元,且不高于60元.销售期间发现,当销售单价定为44元时,每天可售出300个,由于销售火爆,商家决定提价销售.经市场调研发现,销售单价每上涨1元,每天销量减少10个.(1)、求当每个纪念品的销售单价是多少元时,商家每天获利2640元;(2)、将纪念品的销售单价定为多少元时,商家每天销售纪念品获得的利润w元最大?最大利润是多少元?23. 阅读理解:【材料一】若三个非零实数x,y,z中有一个数的平方等于另外两个数的积,则称三个实数x,y,z构成“友好数”.
【材料二】若关于x的一元二次方程的两根分别为 , 则有: .
问题解决:
(1)、实数4,6,9可以构成“友好数”吗?请说明理由;(2)、若三点均在函数(k为常数且)的图象上,且这三点的纵坐标构成“友好数”,求实数t的值;(3)、设三个实数是“友好数”且满足 , 其中是关于x的一元二次方程的两个根,是抛物线与x轴的一个交点的横坐标.①的值等于 ;
②设 , 求y关于x的函数关系式.
24. 平移是一种基本的几何图形变换,利用平移可将分散的条件相对集中,以达到解决问题的目的.如图1,在四边形中, , 若 , 求的值.

小明发现,平移至 , 构造 , 经过推理和计算能够使问题得到解决(如图2).
(1)、【求解体验】请根据小明的思路求的值.
(2)、【尝试应用】如图3,在矩形和中,连结交于点G,连接.若 , 求的度数;
(3)、【拓展延伸】如图4,在(2)的条件下,连结 , 若 , 求的面积.