2022年中考数学真题分类汇编：10 一元二次方程

试卷更新日期：2022-07-11 类型：二轮复习

进入出卷网下载

一、单选题

1. 已知关于 $x$ 的一元二次方程 $x^{2} - 2 x - a = 0$ 的两根分别记为 $x_{1}$ ， $x_{2}$ ，若 $x_{1} = - 1$ ，则 $a - x_{1}^{2} - x_{2}^{2}$ 的值为（）

A、7 B、-7 C、6 D、-6

查看试题解析
2. 2022年北京冬奥会女子冰壶比赛有若干支队伍参加了单循环比赛，单循环比赛共进行了45场，共有多少支队伍参加比赛？（）

A、8 B、10 C、7 D、9

查看试题解析
3. 若关于 $x$ 的一元二次方程 $a x^{2} + 2 x - 1 = 0$ 有两个不相等的实数根，则 $a$ 的取值范围是（）

A、 $a \neq 0$ B、 $a > - 1$ 且 $a \neq 0$ C、 $a \geq - 1$ 且 $a \neq 0$ D、 $a > - 1$

查看试题解析
4. 已知 $m$ 、 $n$ 是一元二次方程 $x^{2} + 2 x - 5 = 0$ 的两个根，则 $m^{2} + m n + 2 m$ 的值为（）

A、0 B、-10 C、3 D、10

查看试题解析
5. 关于 $x$ 的一元二次方程 $x^{2} - 4 x + k = 0$ 无实数解，则 $k$ 的取值范围是（）

A、 $k > 4$ B、 $k < 4$ C、 $k < - 4$ D、 $k > 1$

查看试题解析
6. 方程 $x^{2} + 4 x + 3 = 0$ 的两个根为（）

A、 $x_{1} = 1 ， x_{2} = 3$ B、 $x_{1} = - 1 ， x_{2} = 3$ C、 $x_{1} = 1 ， x_{2} = - 3$ D、 $x_{1} = - 1 ， x_{2} = - 3$

查看试题解析
7. 下列一元二次方程有实数解的是（）

A、2x²﹣x+1＝0 B、x²﹣2x+2＝0 C、x²+3x﹣2＝0 D、x²+2＝0

查看试题解析
8. 关于x的一元二次方程 $3 x^{2} - 2 x + m = 0$ 有两根，其中一根为 $x = 1$ ，则这两根之积为（）

A、 $\frac{1}{3}$ B、 $\frac{2}{3}$ C、1 D、 $- \frac{1}{3}$

查看试题解析
9. 临近春节的三个月，某干果店迎来了销售旺季，第一个月的销售额为8万元，第三个月的销售额为11.52万元，设这两个月销售额的月平均增长率为x，则根据题意，可列方程为（）

A、 $8 (1 + 2 x) = 11.52$ B、 $2 \times 8 (1 + x) = 11.52$ C、 $8 (1 + x)^{2} = 11.52$ D、 $8 (1 + x^{2}) = 11.52$

查看试题解析
10. 若关于x的一元二次方程 $x^{2} + x - k = 0$ 有两个实数根，则k的取值范围是（）

A、 $k > - \frac{1}{4}$ B、 $k \geq - \frac{1}{4}$ C、 $k < - \frac{1}{4}$ D、 $k \leq - \frac{1}{4}$

查看试题解析
11. 一元二次方程 $2 x^{2} - 5 x + 6 = 0$ 的根的情况为（）

A、无实数根 B、有两个不等的实数根 C、有两个相等的实数根 D、不能判定

查看试题解析
12. 若关于x的方程x²+6x+c=0有两个相等的实数根，则c的值是（）

A、36 B、-36 C、9 D、-9

查看试题解析
13. 已知m为方程x²+3x﹣2022＝0的根，那么m³+2m²﹣2025m+2022的值为（）

A、﹣2022 B、0 C、2022 D、4044

查看试题解析
14. 学校连续三年组织学生参加义务植树，第一年共植树 400 棵，第三年共植树 625 棵．设该校植树棵数的年平均增长率为 x，根据题意，下列方程正确的是（）

A、 $625 {(1 - x)}^{2} = 400$ B、 $400 {(1 + x)}^{2} = 625$ C、 $625 x^{2} = 400$ D、 $400 x^{2} = 625$

查看试题解析
15. 小区新增了一家快递店，第一天揽件200件，第三天揽件242件，设该快递店揽件日平均增长率为x，根据题意，下面所列方程正确的是（）

A、 $200 {(1 + x)}^{2} = 242$ B、 $200 {(1 - x)}^{2} = 242$ C、 $200 (1 + 2 x) = 242$ D、 $200 (1 - 2 x) = 242$

查看试题解析

二、填空题

16. 关于x的一元二次方程 $x^{2} + 2 x + t = 0$ 有两个不相等的实数根，则实数t的值为.

查看试题解析
17. 已知关于 $x$ 的一元二次方程 $x^{2} + 2 x + m = 0$ 有两个不相等的实数根，则实数 $m$ 的取值范围是.

查看试题解析
18. 若关于x的一元二次方程 $x^{2} - 4 x + m - 1 = 0$ 有两个不相等的实数根，则m的取值范围是．

查看试题解析
19. 设 $x_{1}$ 与 $x_{2}$ 为一元二次方程 $\frac{1}{2} x^{2} + 3 x + 2 = 0$ 的两根，则 ${(x_{1} - x_{2})}^{2}$ 的值为．

查看试题解析
20. 若 $x = 1$ 是方程 $x^{2} - 2 x + a = 0$ 的根，则 $a =$ ．

查看试题解析
21. 若一元二次方程 $x^{2} - 4 x + 3 = 0$ 的两个根是 $x_{1}$ ， $x_{2}$ ，则 $x_{1} \cdot x_{2}$ 的值是.

查看试题解析

三、计算题

22. 解方程： $(2 x + 3)^{2} = (3 x + 2)^{2}$

查看试题解析

四、综合题

23. 某造纸厂为节约木材，实现企业绿色低碳发展，通过技术改造升级，使再生纸项目的生产规模不断扩大.该厂3，4月份共生产再生纸800吨，其中4月份再生纸产量是3月份的2倍少100吨.

(1)、求4月份再生纸的产量；

(2)、若4月份每吨再生纸的利润为1000元，5月份再生纸产量比上月增加 $m %$ .5月份每吨再生纸的利润比上月增加 $\frac{m}{2} %$ ，则5月份再生纸项目月利润达到66万元.求 $m$ 的值；

(3)、若4月份每吨再生纸的利润为1200元，4至6月每吨再生纸利润的月平均增长率与6月份再生纸产量比上月增长的百分数相同，6月份再生纸项目月利润比上月增加了 $2 5%$ .求6月份每吨再生纸的利润是多少元？

查看试题解析
24. 已知关于x的一元二次方程 $x^{2} + (2 k + 1) x + k^{2} + 1 = 0$ 有两个不等实数根 $x_{1}$ ， $x_{2}$ .

(1)、求k的取值范围；

(2)、若 $x_{1} x_{2} = 5$ ，求k的值.

查看试题解析
25. 建设美丽城市，改造老旧小区.某市2019年投入资金1000万元，2021年投入资金1440万元，现假定每年投入资金的增长率相同.

(1)、求该市改造老旧小区投入资金的年平均增长率；

(2)、2021年老旧小区改造的平均费用为每个80万元.2022年为提高老旧小区品质，每个小区改造费用增加15%.如果投入资金年增长率保持不变，求该市在2022年最多可以改造多少个老旧小区？

查看试题解析
26. 阅读材料：十六世纪的法国数学家弗朗索瓦·韦达发现了一元二次方程的根与系数之间的关系，可表述为“当判别式 $△ \geq 0$ 时，关于 $x$ 的一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 的两个根 $x_{1}$ 、 $x_{2}$ 有如下关系： $x_{1} + x_{2} = - \frac{b}{a}$ ， $x_{1} x_{2} = \frac{c}{a}$ ”.此关系通常被称为“韦达定理”.已知二次函数 $y = a x^{2} + b x + c (a > 0)$ .

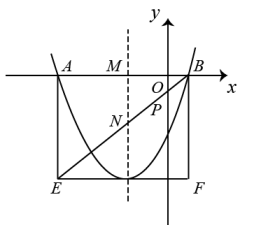(1)、若 $a = 1$ ， $b = 3$ ，且该二次函数的图象过点 $(1 ， 1)$ ，求 $c$ 的值；

(2)、如图所示，在平面直角坐标系 $O x y$ 中，该二次函数的图象与 $x$ 轴相交于不同的两点 $A (x_{1} ， 0)$ 、 $B (x_{2} ， 0)$ ，其中 $x_{1} < 0 < x_{2}$ 、 $| x_{1} | > | x_{2} |$ ，且该二次函数的图象的顶点在矩形 $A B F E$ 的边 $E F$ 上，其对称轴与 $x$ 轴、 $B E$ 分别交于点 $M$ 、 $N$ ， $B E$ 与 $y$ 轴相交于点 $P$ ，且满足 $t a n ∠ A B E = \frac{3}{4}$ .
①求关于 $x$ 的一元二次方程 $a x^{2} + b x + c = 0$ 的根的判别式的值；
②若 $N P = 2 B P$ ，令 $T = \frac{1}{a^{2}} + \frac{16}{5} c$ ，求 $T$ 的最小值.

查看试题解析