2022年中考数学真题分类汇编：08 二元一次方程组

试卷更新日期：2022-07-11 类型：二轮复习

进入出卷网下载

一、单选题

1. 国家“双减”政策实施后，某校开展了丰富多彩的社团活动．某班同学报名参加书法和围棋两个社团，班长为参加社团的同学去商场购买毛笔和围棋（两种都购买）共花费360元．其中毛笔每支15元，围棋每副20元，共有多少种购买方案？（）

A、5 B、6 C、7 D、8

查看试题解析
2. 端午节前夕，某食品加工厂准备将生产的粽子装入A、B两种食品盒中，A种食品盒每盒装8个粽子，B种食品盒每盒装10个粽子，若现将200个粽子分别装入A、B两种食品盒中（两种食品盒均要使用并且装满），则不同的分装方式有（）

A、2种 B、3种 C、4种 D、5种

查看试题解析
3. 五一小长假，小华和家人到公园游玩.湖边有大小两种游船.小华发现1艘大船与2艘小船一次共可以满载游客32人，2艘大船与1艘小船一次共可以满载游客46人.则1艘大船与1艘小船一次共可以满载游客的人数为（）

A、30 B、26 C、24 D、22

查看试题解析
4. 为培养青少年的创新意识、动手实践能力、现场应变能力和团队精神，湘潭市举办了第10届青少年机器人竞赛.组委会为每个比赛场地准备了四条腿的桌子和三条腿的凳子共12个，若桌子腿数与凳子腿数的和为40条，则每个比赛场地有几张桌子和几条凳子？设有x张桌子，有y条凳子，根据题意所列方程组正确的是（）

A、 ${\begin{array}{l} x + y = 40 \\ 4 x + 3 y = 12 \end{array}$ B、 ${\begin{array}{l} x + y = 12 \\ 4 x + 3 y = 40 \end{array}$ C、 ${\begin{array}{l} x + y = 40 \\ 3 x + 4 y = 12 \end{array}$ D、 ${\begin{array}{l} x + y = 12 \\ 3 x + 4 y = 40 \end{array}$

查看试题解析
5. 幻方是古老的数学问题，我国古代的《洛书》中记载了最早的幻方——九宫格.将9个数填入幻方的空格中，要求每一横行、每一竖列以及两条对角线上的3个数之和相等，例如图（1）就是一个幻方.图（2）是一个未完成的幻方，则 $x$ 与 $y$ 的和是（）

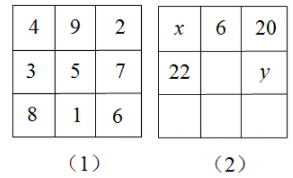A、9 B、10 C、11 D、12

查看试题解析
6. 对于二元一次方程组 ${\begin{array}{l} y = x - 1 ① \\ x + 2 y = 7 ② \end{array}$ ，将①式代入②式，消去 $y$ 可以得到（）

A、 $x + 2 x - 1 = 7$ B、 $x + 2 x - 2 = 7$ C、 $x + x - 1 = 7$ D、 $x + 2 x + 2 = 7$

查看试题解析
7. 我国古代数学名著《九章算术》记载：“今有牛五、羊二，直金十九两；牛二、羊三，直金十二两.问牛、羊各直金几何？”题目大意是：5头牛、2只羊共19两银子；2头牛、3只羊共12两银子，每头牛、每只羊各多少两银子？设1头牛 $x$ 两银子，1只羊 $y$ 两银子，则可列方程组为（）

A、 ${\begin{array}{l} 5 x + 2 y = 19 \\ 2 x + 3 y = 12 \end{array}$ B、 ${\begin{array}{l} 5 x + 2 y = 12 \\ 2 x + 3 y = 19 \end{array}$ C、 ${\begin{array}{l} 2 x + 5 y = 19 \\ 3 x + 2 y = 12 \end{array}$ D、 ${\begin{array}{l} 2 x + 5 y = 12 \\ 3 x + 2 y = 19 \end{array}$

查看试题解析
8. 我国古代《算法统宗》里有这样一首诗：“我问开店李三公，众客都来到店中，一房七客多七客，一房九客一房空.”诗中后面两句的意思是：如果一间客房住7人，那么有7人无房可住；如果一间客房住9人，那么就空出一间客房，若设该店有客房x间，房客y人，则列出关于x、y的二元一次方程组正确的是（）

A、 ${\begin{array}{l} 7 x - 7 = y \\ 9 (x - 1) = y \end{array}$ B、 ${\begin{array}{l} 7 x + 7 = y \\ 9 (x - 1) = y \end{array}$ C、 ${\begin{array}{l} 7 x + 7 = y \\ 9 x - 1 = y \end{array}$ D、 ${\begin{array}{l} 7 x - 7 = y \\ 9 x - 1 = y \end{array}$

查看试题解析
9. 《孙子算经》是我国古代经典数学名著，其中有一道“鸡兔同笼”问题：“今有鸡兔同笼，上有三十五头，下有九十四足.问鸡兔各几何？”学了方程（组）后，我们可以非常顺捷地解决这个问题，如果设鸡有 $x$ 只，兔有 $y$ 只，那么可列方程组为（）

A、 ${\begin{array}{l} x + y = 35 \\ 4 x + 4 y = 94 \end{array}$ B、 ${\begin{array}{l} x + y = 35 \\ 4 x + 2 y = 94 \end{array}$ C、 ${\begin{array}{l} x + y = 94 \\ 4 x + 4 y = 35 \end{array}$ D、 ${\begin{array}{l} x + y = 35 \\ 2 x + 4 y = 94 \end{array}$

查看试题解析
10. “市长杯”青少年校园足球联赛的比赛规则是：胜一场得3分，平一场得1分，负一场得0分．某校足球队在第一轮比赛中赛了9场，只负了2场，共得17分．那么该队胜了几场，平了几场？设该队胜了x场，平了y场，根据题意可列方程组为（）

A、 ${\begin{cases} x + y = 7 ， \\ 3 x + y = 17. \end{cases}$ B、 ${\begin{cases} x + y = 9 ， \\ 3 x + y = 17. \end{cases}$ C、 ${\begin{cases} x + y = 7 ， \\ x + 3 y = 17. \end{cases}$ D、 ${\begin{cases} x + y = 9 ， \\ x + 3 y = 17. \end{cases}$

查看试题解析
11. 我国古代数学名著《九章算术》中记载：“粟米之法：粟率五十；粝米三十．今有米在十斗桶中，不知其数．满中添粟而春之，得米七斗，问故米几何？”意思为： 50 斗谷子能出30斗米，即出米率为 $\frac{3}{5}$ ．今有米在容量为10斗的桶中，但不知道数量是多少．再向桶中加满谷子，再舂成米，共得米7斗．问原米有米多少斗？如果设原来有米x斗，向桶中加谷子y斗，那么可列方程组为（）

A、 ${\begin{cases} x + y = 10 \\ x + \frac{3}{5} y = 7 \end{cases}$ B、 ${\begin{cases} x + y = 10 \\ \frac{3}{5} x + y = 7 \end{cases}$ C、 ${\begin{cases} x + y = 7 \\ x + \frac{3}{5} y = 10 \end{cases}$ D、 ${\begin{cases} x + y = 7 \\ \frac{3}{5} x + y = 10 \end{cases}$

查看试题解析
12. 某体育比赛的门票分A票和B票两种，A票每张x元，B票每张y元．已知10张A票的总价与19张B票的总价相差320元，则（）

A、 $| \frac{10 x}{19 y} | = 320$ B、 $| \frac{10 y}{19 x} | = 320$ C、|10x-19y|=320 D、|19x-10y|=320

查看试题解析
13. 中国清代算书《御制数理精蕴》中有这样一题：“马四匹、牛六头，共价四十八两（‘两’为我国古代货币单位）；马二匹、牛五头，共价三十八两，阀马、牛各价几何？”设马每匹x两，牛每头y两，根据题意可列方程组为（）

A、 ${\begin{array}{l} 4 x + 6 y = 38 \\ 2 x + 5 y = 48 \end{array}$ B、 ${\begin{array}{l} 4 x + 6 y = 48 \\ 2 x + 5 y = 38 \end{array}$ C、 ${\begin{array}{l} 4 x + 6 y = 48 \\ 5 x + 2 y = 38 \end{array}$ D、 ${\begin{array}{l} 4 y + 6 x = 48 \\ 2 y + 5 x = 38 \end{array}$

查看试题解析
14. 上学期某班的学生都是双人桌，其中 $\frac{1}{4}$ 男生与女生同桌，这些女生占全班女生的 $\frac{1}{5}$ 。本学期该班新转入4个男生后，男女生刚好一样多，设上学期该班有男生x人，女生y人．根根据题意可得方程组为（）

A、 ${\begin{cases} x + 4 = y \\ \frac{x}{4} = \frac{y}{5} \end{cases}$ B、 ${\begin{cases} x + 4 = y \\ \frac{x}{5} = \frac{y}{4} \end{cases}$ C、 ${\begin{cases} x - 4 = y \\ \frac{x}{4} = \frac{y}{5} \end{cases}$ D、 ${\begin{cases} x - 4 = y \\ \frac{x}{5} = \frac{y}{4} \end{cases}$

查看试题解析

二、填空题

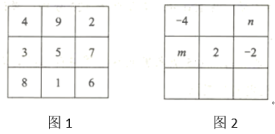
15. 幻方的历史很悠久，传说最早出现在夏禹时代的“洛书”．把洛书用今天的数学符号翻译出来，就是一个三阶幻方（如图1），将9个数填在3×3（三行三列）的方格中，如果满足每个横行、每个竖列、每条对角线上的三个数字之和都相等，就得到一个广义的三阶幻方．图2的方格中填写了一些数字和字母，若能构成一个广义的三阶幻方，则mn＝．

查看试题解析
16. 某班为奖励在数学竞赛中成绩优异的同学，花费48元钱购买了甲、乙两种奖品，每种奖品至少购买1件，其中甲种奖品每件4元，乙种奖品每件3元，则有种购买方案．

查看试题解析
17. 已知二元一次方程组 ${\begin{array}{l} x + 2 y = 4 \\ 2 x + y = 5 \end{array}$ ，则 $x - y$ 的值为.

查看试题解析
18. 特产专卖店销售桃片、米花糖、麻花三种特产，其中每包桃片的成本是麻花的 2 倍，每包桃片、米花糖、麻花的售价分别比其成本高 20%、30%、20%．该店五月份销售桃片、米花糖、麻花的数量之比为 1：3：2，三种特产的总利润是总成本的 25%，则每包米花糖与每包麻花的成本之比为．

查看试题解析

三、计算题

19. 解方程组： ${\begin{array}{l} x + 2 y = 4 \\ x + 3 y = 5 \end{array}$ ．

查看试题解析

四、解答题

20. 我省某村委会根据“十四五”规划的要求，打造乡村品牌，推销有机黑胡椒和有机白胡椒.已知每千克有机黑胡椒比每千克有机白胡椒的售价便宜10元，购买2千克有机黑胡椒和3千克有机白胡椒需付280元，求每千克有机黑胡椒和每千克有机白胡椒的售价.

查看试题解析