2022年中考数学真题分类汇编：03 代数式

试卷更新日期：2022-07-11 类型：二轮复习

进入出卷网下载

一、单选题

1. 为落实“双减”政策，某校利用课后服务开展了主题为“书香满校园”的读书活动.现需购买甲，乙两种读本共100本供学生阅读，其中甲种读本的单价为10元/本，乙种读本的单价为8元/本，设购买甲种读本x本，则购买乙种读本的费用为（）

A、 $8 x$ 元 B、 $10 (100 - x)$ 元 C、 $8 (100 - x)$ 元 D、 $(100 - 8 x)$ 元

查看试题解析
2. 生物学中，描述、解释和预测种群数量的变化，常常需要建立数学模型.在营养和生存空间没有限制的情况下，某种细胞可通过分裂来繁殖后代，我们就用数学模型2ⁿ来表示.即：2¹＝2，2²＝4，2³＝8，2⁴＝16，2⁵＝32，……，请你推算2²⁰²²的个位数字是（）

A、8 B、6 C、4 D、2

查看试题解析
3. 若 $1 0^{x} = N$ ，则称 $x$ 是以10为底 $N$ 的对数.记作： $x = l g N$ .例如： $1 0^{2} = 100$ ，则 $2 = l g 100$ ； $1 0^{0} = 1$ ，则 $0 = l g 1$ .对数运算满足：当 $M > 0$ ， $N > 0$ 时， $l g M + l g N = l g (M N)$ ，例如： $l g 3 + l g 5 = l g 15$ ，则 ${(l g 5)}^{2} + l g 5 \times l g 2 + l g 2$ 的值为（）

A、5 B、2 C、1 D、0

查看试题解析
4. 我们发现： $\sqrt{6 + 3} = 3$ ， $\sqrt{6 + \sqrt{6 + 3}} = 3$ ， $\sqrt{6 + \sqrt{6 + \sqrt{6 + 3}}} = 3$ ， …， $\underset{n 个根号}{\underset{︸}{\sqrt{6 + \sqrt{6 + \sqrt{6 + ⋯ + \sqrt{6 + \sqrt{6 + 3}}}}} = 3}}$ ，一般地，对于正整数 $a$ ， $b$ ，如果满足 $\underset{n 个根号}{\underset{︸}{\sqrt{b + \sqrt{b + \sqrt{b + ⋯ + \sqrt{b + \sqrt{b + a}}}}} = a}}$ 时，称 $(a ， b)$ 为一组完美方根数对.如上面 $(3 ， 6)$ 是一组完美方根数对.则下面4个结论：① $(4 ， 12)$ 是完美方根数对；② $(9 ， 91)$ 是完美方根数对；③若 $(a ， 380)$ 是完美方根数对，则 $a = 20$ ；④若 $(x ， y)$ 是完美方根数对，则点 $P (x ， y)$ 在抛物线 $y = x^{2} - x$ 上.其中正确的结论有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 将字母“C”，“H”按照如图所示的规律摆放，依次下去，则第4个图形中字母“H”的个数是（）

A、9 B、10 C、11 D、12

查看试题解析
6. 将全体正偶数排成一个三角形数阵：
按照以上排列的规律，第10行第5个数是（）

A、98 B、100 C、102 D、104

查看试题解析
7. 一个垃圾填埋场，它在地面上的形状为长80m，宽60m 的矩形，有污水从该矩形的四周边界向外渗透了3m ，则该垃圾填埋场外围受污染土地的面积为（）

A、 $(840 + 6 π) m^{2}$ B、 $(840 + 9 π) m^{2}$ C、 $840 m^{2}$ D、 $876 m^{2}$

查看试题解析
8. 按一定规律排列的单项式：x，3x²，5x³，7x⁴ ， 9x⁵ ， ……，第n个单项式是（）

A、(2n-1) xⁿ B、(2n+1)xⁿ C、(n-1)xⁿ D、(n+1)xⁿ

查看试题解析
9. 把菱形按照如图所示的规律拼图案，其中第①个图案中有 1个菱形，第②个图案中有 3个菱形，第③个图案中有5个菱形，…，按此规律排列下去，则第⑥个图案中菱形的个数为（）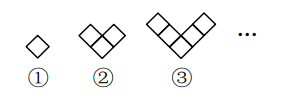

A、15 B、13 C、11 D、9

查看试题解析
10. 对多项式x-y-z-m-n任意加括号后仍然只含减法运算并将所得式子化简，称之为“加算操作”，例如：(x-y)-(z-m-n)=x-y-z+m+n，x-y-(z-m)-n = x-y-z+m-n，……，
给出下列说法：

①至少存在一种“加算操作”，使其结果与原多项式相等； ②不存在任何“加算操作”，使其结果与原多项式之和为0； ③所有的“加算操作”共有 8 种不同的结果．以上说法中正确的个数为（）

A、0 B、1 C、2 D、3

查看试题解析
11. 用正方形按如图所示的规律拼图案，其中第①企图案中有5个正方形，第②个图案中有9个正方形，第③全图案中有13全正方形，第④个图案中有17企正方形，此规律排列下去，则第⑨个图案中正方形的个数为（）

A、32 B、34 C、37 D、41

查看试题解析

二、填空题

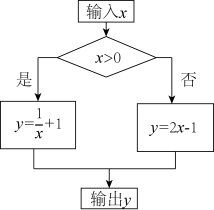
12. 阅读材料：整体代值是数学中常用的方法.例如“已知 $3 a - b = 2$ ，求代数式 $6 a - 2 b - 1$ 的值.”可以这样解： $6 a - 2 b - 1 = 2 (3 a - b) - 1 = 2 \times 2 - 1 = 3$ .根据阅读材料，解决问题：若 $x = 2$ 是关于x的一元一次方程 $a x + b = 3$ 的解，则代数式 $4 a^{2} + 4 a b + b^{2} + 4 a + 2 b - 1$ 的值是.

查看试题解析
13. 若 ${(2 x + y - 5)}^{2} + \sqrt{x + 2 y + 4} = 0$ ，则 $x - y$ 的值是.

查看试题解析
14. 按照如图所示的程序计算，若输出y的值是2，则输入x的值是．

查看试题解析
15. 如图， $∠ A O B = 60 °$ ，点 $P_{1}$ 在射线 $O A$ 上，且 $O P_{1} = 1$ ，过点 $P_{1}$ 作 $P_{1} K_{1} ⊥ O A$ 交射线 $O B$ 于 $K_{1}$ ，在射线 $O A$ 上截取 $P_{1} P_{2}$ ，使 $P_{1} P_{2} = P_{1} K_{1}$ ；过点 $P_{2}$ 作 $P_{2} K_{2} ⊥ O A$ 交射线 $O B$ 于 $K_{2}$ ，在射线 $O A$ 上截取 $P_{2} P_{3}$ ，使 $P_{2} P_{3} = P_{2} K_{2}$ .按照此规律，线段 $P_{2023} K_{2023}$ 的长为．

查看试题解析
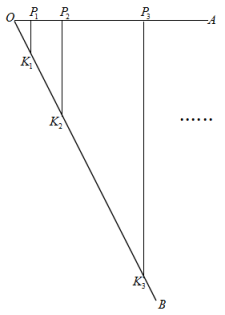16. 定义一种运算； $s i n (α + β) = s i n α c o s β + c o s α s i n β$ ， $s i n (α - β) = s i n α c o s β - c o s α s i n β$ ．例如：当 $α = 45 °$ ， $β = 30 °$ 时， $s i n (45 ° + 30 °) =$ $\frac{\sqrt{2}}{2} \times \frac{\sqrt{3}}{2} + \frac{\sqrt{2}}{2} \times \frac{1}{2} = \frac{\sqrt{6} + \sqrt{2}}{4}$ ，则 $s i n 15 °$ 的值为．

查看试题解析
17. 定义：一个三角形的一边长是另一边长的2倍，这样的三角形叫做“倍长三角形”.若等腰△ABC是“倍长三角形”，底边BC的长为3，则腰AB的长为.

查看试题解析
18. 将一组数 $\sqrt{2}$ ， 2， $\sqrt{6}$ ， $2 \sqrt{2}$ ， …， $4 \sqrt{2}$ ，按下列方式进行排列：
$\sqrt{2}$ ， 2， $\sqrt{6}$ ， $2 \sqrt{2}$ ；
$\sqrt{10}$ ， $2 \sqrt{3}$ ， $\sqrt{14}$ ， 4；
…
若2的位置记为 $(1 ， 2)$ ， $\sqrt{14}$ 的位置记为 $(2 ， 3)$ ，则 $2 \sqrt{7}$ 的位置记为.

查看试题解析
19. 按规律排列的单项式： $x$ ， $- x^{3}$ ， $x^{5}$ ， $- x^{7}$ ， $x^{9}$ ， …，则第20个单项式是.

查看试题解析
20. 正偶数2，4，6，8，10，…，按如下规律排列，
则第27行的第21个数是 .

查看试题解析

三、综合题

21. 设 $\bar{a 5}$ 是一个两位数，其中a是十位上的数字（1≤a≤9）．例如，当a＝4时， $\bar{a 5}$ 表示的两位数是45．

(1)、尝试：
①当a＝1时，15²＝225＝1×2×100＋25；

②当a＝2时，25²＝625＝2×3×100＋25；

③当a＝3时，35²＝1225＝；

……

(2)、归纳： ${\bar{a 5}}^{2}$ 与100a(a＋1)＋25有怎样的大小关系？试说明理由．

(3)、运用：若 ${\bar{a 5}}^{2}$ 与100a的差为2525，求a的值．

查看试题解析
22. 观察以下等式：
第1个等式： ${(2 \times 1 + 1)}^{2} = {(2 \times 2 + 1)}^{2} - {(2 \times 2)}^{2}$ ，
第2个等式： ${(2 \times 2 + 1)}^{2} = {(3 \times 4 + 1)}^{2} - {(3 \times 4)}^{2}$ ，
第3个等式： ${(2 \times 3 + 1)}^{2} = {(4 \times 6 + 1)}^{2} - {(4 \times 6)}^{2}$ ，
第4个等式： ${(2 \times 4 + 1)}^{2} = {(5 \times 8 + 1)}^{2} - {(5 \times 8)}^{2}$ ，
……
按照以上规律．解决下列问题：

(1)、写出第5个等式：；

(2)、写出你猜想的第n个等式（用含n的式子表示），并证明．

查看试题解析
23. 如图1，将长为2a+3，宽为2a的矩形分割成四个全等的直角三角形，拼成“赵爽弦图”(如图2)，得到大小两个正方形，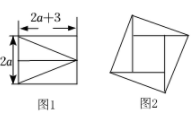

(1)、用关于a的代数式表示图2中小正方形的边长

(2)、当a=3时，该小正方形的面积是多少？

查看试题解析
24. 对于一个各数位上的数字均不为 0 的三位自然数 N，若 N 能被它的各数位上的数字之和 m 整除，则称 N 是 m 的“和倍数”．
例如：∵247÷(2+4+7)= 247÷13=19，∴247是13的“和倍数”.

又如： ∵214÷(2+1+4)=214÷7=30……4，∴214不是“和倍数”.

(1)、判断 357，441 是否是“和倍数”？说明理由；

(2)、三位数 A是12的“和倍数”，a，b，c 分别是数 A其中一个数位上的数字，且 a>b>c在 a，b，c 中任选两个组成两位数，其中最大的两位数记为 F (A)，最小的两位数记为 G(A)，若 $\frac{F (A) + G (A)}{16}$ 为整数，求出满足条件的所有数 A．

查看试题解析