2022年中考数学真题分类汇编：01 有理数

试卷更新日期：2022-07-11 类型：二轮复习

进入出卷网下载

一、单选题

1. 下列各数中，-1的相反数是（）

A、-1 B、0 C、1 D、2

查看试题解析
2. 如图，数轴上的点A表示的数是 $- 1$ ，则点A关于原点对称的点表示的数是（）

A、-2 B、0 C、1 D、2

查看试题解析
3. 为了加快构建清洁低碳、安全高效的能源体系，国家发布《关于促进新时代新能源高质量发展的实施方案》，旨在锚定到2030年我国风电、太阳能发电总装机容量达到1200000000千瓦以上的目标.数据1200000000用科学记数法表示为（）

A、 $1.2 \times 1 0^{10}$ B、 $1.2 \times 1 0^{9}$ C、 $1.2 \times 1 0^{8}$ D、 $12 \times 1 0^{8}$

查看试题解析
4. 下列说法中，正确的是（）

A、2与-2互为倒数 B、2与 $\frac{1}{2}$ 互为相反数 C、0的相反数是0 D、2的绝对值是-2

查看试题解析
5. 化简 $| - \frac{1}{2} |$ ，下列结果中，正确的是（）

A、 $\frac{1}{2}$ B、 $- \frac{1}{2}$ C、2 D、-2

查看试题解析
6. -2022的倒数是（）

A、2022 B、 $- 2022$ C、 $\frac{1}{2022}$ D、 $- \frac{1}{2022}$

查看试题解析
7. 计算 $2^{2}$ 的结果是（）

A、1 B、 $\sqrt{2}$ C、2 D、4

查看试题解析
8. 已知抛物线 $y = a x^{2} + b x + c$ 的图象与 $x$ 轴交于点 $A (- 2 ， 0)$ 、 $B (4 ， 0)$ ，若以 $A B$ 为直径的圆与在 $x$ 轴下方的抛物线有交点，则 $a$ 的取值范围是（）

A、 $a \geq \frac{1}{3}$ B、 $a > \frac{1}{3}$ C、 $0 < a < \frac{1}{3}$ D、 $0 < a \leq \frac{1}{3}$

查看试题解析
9. -5的绝对值是（）

A、5 B、-5 C、 $- \frac{1}{5}$ D、 $\frac{1}{5}$

查看试题解析
10. 与 $- 3 \frac{1}{2}$ 相等的是（）

A、 $- 3 - \frac{1}{2}$ B、 $3 - \frac{1}{2}$ C、 $- 3 + \frac{1}{2}$ D、 $3 + \frac{1}{2}$

查看试题解析
11. 2020年12月17日，我国嫦娥五号返回器携带着月球样本玄武岩成功着陆地球.2021年10月19日，中国科学院发布了一项研究成果：中国科学家测定，嫦娥五号带回的玄武岩形成的年龄为 $20.30 \pm 0.04$ 亿年.用科学记数法表示此玄武岩形成的年龄最小的为（）（单位：年）

A、 $2.034 \times 1 0^{8}$ B、 $2.034 \times 1 0^{9}$ C、 $2.026 \times 1 0^{8}$ D、 $2.026 \times 1 0^{9}$

查看试题解析
12. 若x和y互为倒数，则 $(x + \frac{1}{y}) (2 y - \frac{1}{x})$ 的值是（）

A、1 B、2 C、3 D、4

查看试题解析
13. 下列运算正确的是（）

A、 $\sqrt{{(- 7)}^{2}} = - 7$ B、 $6 \div \frac{2}{3} = 9$ C、 $2 a + 2 b = 2 a b$ D、 $2 a \cdot 3 b = 5 a b$

查看试题解析
14. 如图，点A、B表示的实数互为相反数，则点B表示的实数是（）

A、2 B、﹣2 C、 $\frac{1}{2}$ D、﹣ $\frac{1}{2}$

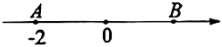查看试题解析
15. 在古代，人们通过在绳子上打结来计数.即“结绳计数”.当时有位父亲为了准确记录孩子的出生天数，在粗细不同的绳子上打结（如图），由细到粗（右细左粗），满七进一，那么孩子已经出生了（）

A、1335天 B、516天 C、435天 D、54天

查看试题解析

二、填空题

16. 2022年5月14日，编号为B-001J的 $C 919$ 大飞机首飞成功.数据显示， $C 919$ 大飞机的单价约为65300000元，数据653000000用科学记数法表示为.

查看试题解析
17. 某小组6名学生的平均身高为acm，规定超过acm的部分记为正数，不足acm的部分记为负数，他们的身高与平均身高的差值情况记录如下表：
学生序号
1
2
3
4
5
6
身高差值（cm）
+2
x
+3
﹣1
﹣4
﹣1
据此判断，2号学生的身高为 cm．

查看试题解析
18. 中国是世界上首先使用负数的国家.两千多年前战国时期李悝所著的《法经》中已出现使用负数的实例.《九章算术》的“方程”一章，在世界数学史上首次正式引入负数及其加减法运算法则，并给出名为“正负术”的算法.请计算以下涉及“负数”的式子的值： $- 1 - {(- 3)}^{2} =$ .

查看试题解析
19. 计算：3+（﹣2）＝.

查看试题解析
20. 当今大数据时代，“二维码”具有存储量大.保密性强、追踪性高等特点，它己被广泛应用于我们的日常生活中，尤其在全球“新冠”疫情防控期间，区区“二维码”已经展现出无穷威力.看似“码码相同”，实则“码码不同”.通常，一个“二维码”由1000个大大小小的黑白小方格组成，其中小方格专门用做纠错码和其他用途的编码，这相当于1000个方格只有200个方格作为数据码.根据相关数学知识，这200个方格可以生成 $2^{200}$ 个不同的数据二维码，现有四名网友对 $2^{200}$ 的理解如下：
YYDS（永远的神）： $2^{200}$ 就是200个2相乘，它是一个非常非常大的数；

DDDD（懂的都懂）： $2^{200}$ 等于 $20 0^{2}$ ；

JXND（觉醒年代）： $2^{200}$ 的个位数字是6；

QGYW（强国有我）：我知道 $2^{10} = 1024 ， 1 0^{3} = 1000$ ，所以我估计 $2^{200}$ 比 $1 0^{60}$ 大.

其中对 $2^{200}$ 的理解错误的网友是（填写网名字母代号）.

查看试题解析

三、综合题

21. “绿水青山就是金山银山”.科学研究表明：树叶在光合作用后产生的分泌物能够吸附空气中的悬浮颗粒物，具有滞尘净化空气的作用.已知一片银杏树叶一年的平均滞尘量比一片国槐树叶一年的平均滞尘量的2倍少 $4 m g$ ，若一片国槐树叶与一片银杏树叶一年的平均滞尘总量为 $62 m g$ .

(1)、请分别求出一片国槐树叶和一片银杏树叶一年的平均滞尘量；

(2)、娄底市双峰县九峰山森林公园某处有始于唐代的三棵银杏树，据估计三棵银杏树共有约50000片树叶.问这三棵银杏树一年的平均滞尘总量约多少千克？

查看试题解析
22. 某单位准备购买文化用品，现有甲、乙两家超市进行促销活动，该文化用品两家超市的标价均为10元/件，甲超市一次性购买金额不超过400元的不优惠，超过400元的部分按标价的6折售卖；乙超市全部按标价的8折售卖.

(1)、若该单位需要购买30件这种文化用品，则在甲超市的购物金额为元；乙超市的购物金额为元；

(2)、假如你是该单位的采购员，你认为选择哪家超市支付的费用较少？

查看试题解析
23. 计算：(-6) ×( $\frac{2}{3}$ -■)-2³ ．
圆圆在做作业时，发现题中有一个数字被墨水污染了。

(1)、如果被污染的数字是 $\frac{1}{2}$ ．请计算(-6)×( $\frac{2}{3}$ - $\frac{1}{2}$ )-2³ ．

(2)、如果计算结果等于6，求被污染的数字．

查看试题解析
24. 若一个四位数M的个位数字与十位数字的平方和恰好是M去掉个位与十位数字后得到的两位数，则这个四位数M为“勾股和数”．
例如： $M = 2543 ， ∵ 3^{2} + 4^{2} = 25 ， ∴ 2543$ 是“勾股和数”.

又如： $M = 4325 ， ∵ 5^{2} + 2^{2} = 29 ， 29 \neq 43 ， ∴ 4325$ 不是“勾股和数”

(1)、判断2022，5055是否是“勾股和数”，并说明理由；

(2)、一个“勾股和数” $M$ 的千位数字为 $a$ ，百位数字为 $b$ ，十位数字为 $c$ ，个位数字为 $d$ ，记 $G (M) = \frac{c + d}{9} ， P$ $(M) = \frac{| 10 (a - c) + (b - d) |}{3}$ .当 $G (M) ， P (M)$ 均是整数时，求出所有满足条件的 $M$ .

查看试题解析

学生序号	1	2	3	4	5	6
身高差值（cm）	+2	x	+3	﹣1	﹣4	﹣1