（北师大版）2022-2023学年度第一学期九年级数学2.6 应用一元二次方程同步测试

试卷更新日期：2022-07-11 类型：同步测试

进入出卷网下载

一、单选题

1. 如图所示，在一边靠墙（墙足够长）的空地上，修建一个面积为375平方米的矩形临时仓库，仓库一边靠墙，另外三边用总长为55米的栅栏围成，若设栅栏AB的长为x米，则下列各方程中，正确的是（）

A、 $\frac{1}{2}$ x（55﹣x）＝375 B、 $\frac{1}{2}$ x（55﹣2x）＝375 C、x（55﹣2x）＝375 D、x（55﹣x）＝375

查看试题解析
2. 如图，一次函数y=-3x+4的图象交x轴于点A，交y轴于点B，点P在线段AB上（不与点A，B重合），过点P分别作OA和OB的垂线，垂足为C，D．若矩形OCPD的面积为1时，则点P的坐标为（）

A、（ $\frac{1}{3}$ ， 3） B、（ $\frac{1}{2}$ ， 2） C、（ $\frac{1}{2}$ ， 2）和（1，1） D、（ $\frac{1}{3}$ ， 3）和（1，1）

查看试题解析
3. 某种植物的主干长出若干数目的支干，每个支干又长出同样数目的小分支，主干、支干和小分支的总数是157，每个支干长出的小分支数目为（）

A、12 B、11 C、8 D、7

查看试题解析
4. 某超市销售一种饮料，平均每天可售出100箱，每箱利润12元．为了扩大销售，增加利润，超市准备适当降价．据测算，若每箱隆价1元，每天可多售出20箱．若要使每天销售饮料获利1400元，设每箱降价的价钱为x元，则根据题意可列方程（）

A、 $(12 - x) (100 + 20 x) = 1400$ B、 $(12 + x) (100 + 20 x) = 1400$ C、 $(12 - x) (100 - 20 x) = 1400$ D、 $(12 + x) (100 - 20 x) = 1400$

查看试题解析
5. 用一条长 $60 c m$ 的绳子围成一个面积为 $200 c m^{2}$ 的长方形．设长方形的长为 $x c m$ ，则可列方程为（）

A、 $x (30 - x) = 200$ B、 $x (30 + x) = 200$ C、 $x (60 + x) = 200$ D、 $x (60 - x) = 200$

查看试题解析
6. 一个同学经过培训后会做某项实验，回到班级后第一节课他教会了若干个同学，第二节课会做的同学每人又教会了同样多的同学，这样全班共有36人会做这项实验，若设1人每次能教会x名同学，则可列方程为（）

A、x＋（x＋1）x＝36 B、（x＋1）²＝36 C、1＋x＋x²＝36 D、x＋（x＋1）²＝36

查看试题解析
7. 学校计划在长为12m，宽为9m矩形地块的正中间建一座劳动实践大棚．大棚是占地面积为88m²的矩形．建成后，大棚外围留下宽度都相同的区域，这个宽度应设计为（）

A、1.8m B、1.5m C、1m D、0.5m

查看试题解析
8. 文博会期间，某公司调查一种工艺品的销售情况，下面是两位调查员和经理的对话．
小张：该工艺品的进价是每个22元；
小李：当销售价为每个38元时，每天可售出160个；当销售价降低3元时，平均每天将能多售出120个．
经理：为了实现平均每天3640元的销售利润，这种工艺品的销售价应降低多少元？
设这种工艺品的销售价每个应降低x元，由题意可列方程为（）

A、（38﹣x）（160+ $\frac{x}{3}$ ×120）＝3640 B、（38﹣x﹣22）（160+120x）＝3640 C、（38﹣x﹣22）（160+3x×120）＝3640 D、（38﹣x﹣22）（160+ $\frac{x}{3}$ ×120）＝3640

查看试题解析
9. 要组织一次篮球邀请赛，参赛的每两个队之间都要比赛一场，赛程共7天，每天3场比赛．设比赛组织者邀请x个队参赛，则根据题意所列方程正确的是（）

A、 $\frac{1}{2}$ x（x＋1）＝21 B、 $\frac{1}{2}$ x（x－1）＝21 C、x（x＋1）＝21 D、x（x－1）＝21

查看试题解析
10. 如图，学校生物试验园地是长20米，宽15米的长方形，为便于管理，现要在中间开辟一横两纵三条宽均为x米的小道，要使种植面积为252平方米.则列方程为（）

A、（20－x）（15－x）＝252 B、（20－2x）（15－x）＝252 C、（20＋x）（15＋x）＝252 D、（20－2x）（15－x）＋2x2＝252

查看试题解析

二、填空题

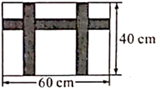
11. 某公司展销如图所示的长方形工艺品，该工艺品长60cm，宽40cm，中间镶有宽度相同的三条丝绸花边，若丝绸花边的面积为650cm² ，设花边的宽度为xcm.根据题意得方程.

查看试题解析
12. 定义：关于x的方程 $a_{1} x^{2} + b_{1} x + c_{1} = 0$ （a₁≠0）与 $a_{2} x^{2} + b_{2} x + c_{2} = 0$ （a₂≠0），如果满足a₁+a₂＝0，b₁＝b₂ ， c₁+c₂＝0，则称这两个方程互为“对称方程”．若关于x的方程 $3 x^{2} + (m^{2} - 2 m + 3) x - 4 = 0$ 与 $- 3 x^{2} + 2 x + n = 0$ 互为“对称方程”，则 $(m - n)^{2}$ 的值为．

查看试题解析
13. 我国南宋数学家杨辉所著《田亩比类乘除捷法》中记载了这样一道题：“直田积八百六十四步，只云阔不及长一十二步，问阔及长各几步．”其大意为：一个矩形的面积为864平方步，宽比长少12步，问宽和长各多少步？设矩形的宽为x步，根据题意，可列方程为．

查看试题解析
14. 老李有一块长方形菜地（长大于宽），面积为180m² ，他利用菜地宽处修了一个宽为3m的蓄水池，修完后老李发现他的菜地刚好变成一个正方形菜地.那么老李原来的菜地周长为m.

查看试题解析
15. 如图，一长为32m、宽为20m的矩形地面上修建有同样宽的道路（图中阴影部分），余下部分进行了绿化.若已知绿化面积为540㎡，则道路的宽为m.

查看试题解析

三、解答题

16. 如图，学校打算用16m的篱笆围成一个长方形的生物园饲养小兔，生物园的一面靠墙（如图，墙长9m），面积是30m² ．求生物园的长和宽．

查看试题解析
17. 某校劳动教育课上，老师让同学们设计劳动基地的规划．如图，在块长 $15 m$ 、宽 $10 m$ 的矩形空地上，修建两条同样宽的相互垂直的道路，剩余部分栽种绿植，要使栽种面积为 $126 m^{2}$ ，则修建的路宽应为多少米？

查看试题解析
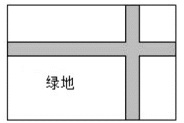18. 益群精品店以每件21元的价格购进一批商品，该商品可以自行定价，若每件商品售价a元，则可卖出 $(350 - 10 a)$ 件，但物价局限定每件商品的利润不得超过20%，商店计划要盈利400元，需要进货多少件商品？每件应定价多少？

查看试题解析
19. 为满足春节市场需求，某商场在节前购进大批某品牌童装，该品牌童装若每件盈利40元，平均每天可售出20件，经调查发现，若每件童装降价1元，商场平均每天可多售出2件，若商场希望该品牌童装日盈利为1200元，同时为了尽量减少库存，请问该童装应降价多少元最合适？

查看试题解析
20. 某校举办了“冰雪运动进校园”活动，计划在校园一块矩形的空地上铺设两块完全相同的矩形冰场．如下图所示，已知空地长27m，宽12m，矩形冰场的长与宽的比为4：3，如果要使冰场的面积是原空地面积的 $\frac{2}{3}$ ，并且预留的上、下通道的宽度相等，左、中、右通道的宽度相等，那么预留的上、下通道的宽度和左、中、右通道的宽度分别是多少米？

查看试题解析
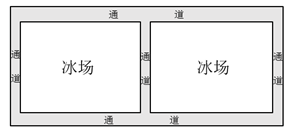21. 第24届冬季奥林匹克运动会将于2022年2月4日在北京开幕，北京成为历史上第一个既举办夏奥会又举办冬奥会的城市．某批发商最近订购了一批具有纪念意义的书签进行销售，平均每天可售出500张，每张可获利0.5元．调查发现，如果每张书签的售价每降价0.1元，平均每天可多售出200张．批发商要想平均每天获利270元，求每张书签应降价多少元．

查看试题解析
22. 如图，利用一面墙(墙EF最长可利用28米)，围成一个矩形花园ABCD．与墙平行的一边BC上要预留2米宽的入口(如图中MN所示，不用砌墙)用60米长的墙的材料，当矩形的长BC为多少米时，矩形花园的面积为300平方米；能否围成480平方米的矩形花园?

查看试题解析
23. 某商品每天可售出300件，每件获利2元．为了尽快减少库存，店主决定降价销售．根据经验可知，如果每件降价0.1元，平均每天可多售出20件，店主要想平均每天获利500元，每件商品应降价多少元？

查看试题解析

（北师大版）2022-2023学年度第一学期九年级数学2.6 应用一元二次方程 同步测试

一、单选题

二、填空题

三、解答题

（北师大版）2022-2023学年度第一学期九年级数学2.6 应用一元二次方程同步测试