（北师大版）2022-2023学年度第一学期八年级数学2.1 认识无理数 同步测试
试卷更新日期：2022-07-10 类型：同步测试
一、单选题
-
1. 在3.14，0， ， ， ，2.010010001…（每两个1之间的0依次增加1个）这六个数中，无理数有（ ）A、2个 B、3个 C、4个 D、5个2. 下列说法错误的是（ ）A、无理数的相反数还是无理数 B、正无理数、负无理数统称为无理数 C、无限小数都是无理数 D、实数与数轴上的点一一对应3. 如图，在4×4的正方形网格中，所有线段的端点都在格点处，则这些线段的长度是无理数的有（ ）
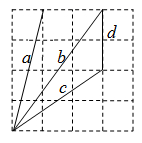A、1 条 B、2条 C、3条 D、4条4. 如图，以数轴的单位长度线段为边作一个正方形，以表示数0的点为圆心，正方形对角线长为半径画弧，交数轴于点A，则点A表示的数是（ ）
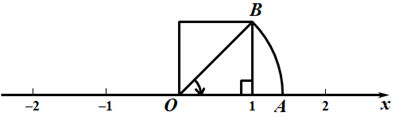A、 B、 C、 D、5. 下列各数中，3.14159， ，0.131131113…（相邻两个3之间1的个数逐次加1个）， ， ， ，无理数的个数有（ ）A、1个 B、2个 C、3个 D、4个6. 下列实数： ，- ，- ，3.14， ， ，0.1010010001……（相邻两个1之间0的个数依次加1）中无理数的个数有（ ）A、1个 B、2个 C、3个 D、4个7. 下列各数中，不是无理数的是（ ）A、 B、 C、 D、0.101001000……（相邻两个1之间0的个数依次加1）8. 要说明命题“两个无理数的和是无理数”，可选择的反例是（ ）A、2，-3 B、 ， C、 ，- D、 ，9. 下列说法正确的是（ ）A、无理数都是无限不循环小数 B、无限小数都是无理数 C、有理数都是有限小数 D、带根号的数都是无理数10. 设 ＝a，则下列结论正确的是（ ）A、4.5＜a＜5.0 B、5.0＜a＜5.5 C、5.5＜a＜6.0 D、6.0＜a＜6.5二、填空题
-
11. 在 中无理数的个数是个．12. 在 ， ， ，3.14，2.12这些数中，无理数是 ．13. 有六张相同的不透明大盾牌，正面写了一个数为0， ，3，14， ， 其中写着无理数的盾牌后面藏着女同学，写着有理数的盾牌后面藏着男同学，这六个盾牌后面藏着个女同学.14. 若无理数a满足1<a<4，请你写出一个符合条件的无理数。15. 若 、 都是无理数，且 ，则 、 的值可以是（填上一组满足条件的值即可）.
三、解答题
-
16. 把下列各数写入相应的集合中：- ， ，0.1， ， ， ，0，0.1212212221．．． （相邻两个1之间2的个数逐次加1）
⑴正数集合{ }；
⑵有理数集合{ }；
⑶无理数集合{ }．
17. 已知长方体的体积是1620，它的长、宽、高的比是5：4：3，问长方体的长、宽、高是无理数吗？为什么？18. 小华家新买了一张边长1.4m的正方形桌子，原有的边长是1m的两块正方形台布都不适用了，但扔掉太可惜，小华想了一个办法，如图，将两块台布拼成一块正方形大台布，请你帮小华计算一下，这块大台布能盖住现在的新桌子吗？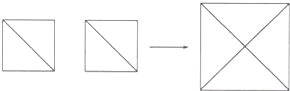
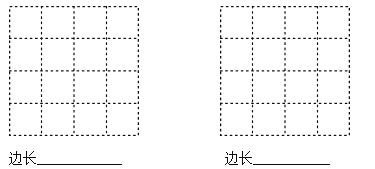
19.如图所示，在4×4的正方形网格中的每个小正方形边长都是1，画出两个边长为无理数的两个正方形，且使它的每个顶点都在小正方形的顶点上．并求出所画正方形的边长．
20. 体积为3的正方体的边长可能是整数吗？可能是分数吗？可能是有理数吗？请说明你的理由．
21. 如图所示，等腰三角形ABC的腰长为3，底边BC的长为4，高AD为h，则h是整数吗？是有理数吗？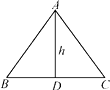
22. 定义：可以表示为两个互质整数的商的形式的数称为有理数，整数可以看作分母为1的有理数；反之为无理数．如不能表示为两个互质的整数的商，所以，是无理数．可以这样证明：
设,a与b 是互质的两个整数，且b≠0．
则a2=2b2因为b是整数且不为0，所以，a是不为0的偶数，设a=2n，（n是整数），所以b2=2n2 ， 所以b也是偶数，与a，b是互质的正整数矛盾．所以，是无理数．仔细阅读上文，然后，请证明：是无理数．
23. 500多年前，数学各学派的学者都认为世界上的数只有整数和分数，直到有一天，大数学家毕达哥拉斯的一个名叫希帕索斯的学生，在研究1和2的比例中项时（若1：x=x：2，那么x叫1和2的比例中项），他怎么也想不出这个比例中项值．后来，他画了一个边长为1的正方形，设对角线为x，于是由毕达哥拉斯定理x2=12+12=2，他想x代表对角线的长，而x2=2，那么x必定是确定的数，这时他又为自己提出了几个问题：（1）x是整数吗？为什么不是？
（2）x可能是分数吗？是，能找出来吗？不是，能说出理由吗？亲爱的同学，你能帮他解答这些问题吗？