(北师大版)2022-2023学年度第一学期八年级数学第1章 勾股定理 单元测试
试卷更新日期:2022-07-10 类型:单元试卷
一、单选题
-
1. 如图,在长方形ABCD中,分别按图中方式放入同样大小的直角三角形纸片.如果按图①方式摆放,刚好放下4个;如果按图②方式摆放,刚好放下3个.若BC=4a,则按图③方式摆放时,剩余部分CF的长为( )
 A、 B、 C、 D、2. 如图,△ABC中,∠C=90°,AD平分∠BAC交BC于点D,DE⊥AB于E,若AB=10cm,AC=6cm,则△BED周长为( )
A、 B、 C、 D、2. 如图,△ABC中,∠C=90°,AD平分∠BAC交BC于点D,DE⊥AB于E,若AB=10cm,AC=6cm,则△BED周长为( ) A、10cm B、12cm C、14cm. D、16cm3. 如图,点A,B都在格点上,若 ,则 的长为( )
A、10cm B、12cm C、14cm. D、16cm3. 如图,点A,B都在格点上,若 ,则 的长为( )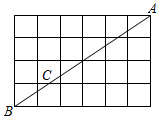 A、 B、 C、 D、4. 如图,长方形纸片ABCD中,AB=3cm,AD=9cm,将此长方形纸片折叠,使点D与点B重合,点C落在点H的位置,折痕为EF , 则△ABE的面积为( )
A、 B、 C、 D、4. 如图,长方形纸片ABCD中,AB=3cm,AD=9cm,将此长方形纸片折叠,使点D与点B重合,点C落在点H的位置,折痕为EF , 则△ABE的面积为( ) A、6cm2 B、8cm2 C、10cm2 D、12cm25. 下列各组数中,以它们为边长的线段能构成直角三角形的是( )A、1,2,3 B、1, , C、4,5,6 D、12,15,206. 在△ABC中,∠A、∠B、∠C的对边分别为a、b、c,若a2=b2+c2 , 则( )A、∠A=90° B、∠B=90° C、∠C=90° D、∠C=∠A+∠B7. 如图,在△ABC中,AB=8,AC=6,BC边的垂直平分线交AB于E,交BC于点D,若CD=5,则AE的长为( )
A、6cm2 B、8cm2 C、10cm2 D、12cm25. 下列各组数中,以它们为边长的线段能构成直角三角形的是( )A、1,2,3 B、1, , C、4,5,6 D、12,15,206. 在△ABC中,∠A、∠B、∠C的对边分别为a、b、c,若a2=b2+c2 , 则( )A、∠A=90° B、∠B=90° C、∠C=90° D、∠C=∠A+∠B7. 如图,在△ABC中,AB=8,AC=6,BC边的垂直平分线交AB于E,交BC于点D,若CD=5,则AE的长为( ) A、 B、2 C、 D、48. 已知 中, 、 、 分别是 、 、 的对边,下列条件中不能判断 是直角三角形的是( )A、 B、 C、 D、9. 如图,小华将升旗的绳子拉紧到旗杆底端点B,绳子末端刚好接触到地面,然后拉紧绳子使其末端到点D处,点D到地面的距离CD长为2m,点D到旗杆AB的水平距离为8m,若设旗杆的高度AB长为xm,则根据题意所列的方程是( ).
A、 B、2 C、 D、48. 已知 中, 、 、 分别是 、 、 的对边,下列条件中不能判断 是直角三角形的是( )A、 B、 C、 D、9. 如图,小华将升旗的绳子拉紧到旗杆底端点B,绳子末端刚好接触到地面,然后拉紧绳子使其末端到点D处,点D到地面的距离CD长为2m,点D到旗杆AB的水平距离为8m,若设旗杆的高度AB长为xm,则根据题意所列的方程是( ). A、 B、 C、 D、10. 国庆假期中,小华与同学去玩探宝游戏,按照探宝图,他们从门口 处出发先往东走 ,又往北走 ,遇到障碍后又往西走 ,再向北走到 处往东拐,仅走了 ,就找到了宝藏,则门口 到藏宝点 的直线距离是( )
A、 B、 C、 D、10. 国庆假期中,小华与同学去玩探宝游戏,按照探宝图,他们从门口 处出发先往东走 ,又往北走 ,遇到障碍后又往西走 ,再向北走到 处往东拐,仅走了 ,就找到了宝藏,则门口 到藏宝点 的直线距离是( ) A、20km B、14km C、11km D、10km
A、20km B、14km C、11km D、10km二、填空题
-
11. 如图,长方形ABCD中,BC=5,AB=3,点E在边BC上,将△DCE沿着DE翻折后,点C落在线段AE上的点F处,那么CE的长度是 .
 12. 如图,AB=4,点M为线段AB上的一个动点,在AB同侧分别以AM和BM为边作等边△AMC和等边△BMD,则线段CD的最小值为 .
12. 如图,AB=4,点M为线段AB上的一个动点,在AB同侧分别以AM和BM为边作等边△AMC和等边△BMD,则线段CD的最小值为 . 13. 在△ABC中,AB=c,AC=b,BC=a,当a、b、c满足时,∠B=90°.14. 如图,在四边形ABCD中, , , , , ,那么四边形ABCD的面积是 .
13. 在△ABC中,AB=c,AC=b,BC=a,当a、b、c满足时,∠B=90°.14. 如图,在四边形ABCD中, , , , , ,那么四边形ABCD的面积是 . 15. 如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A,B,C,D的面积分别为2,5,1,2.则图中所有正方形的面积和是 .
15. 如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A,B,C,D的面积分别为2,5,1,2.则图中所有正方形的面积和是 .
三、解答题
-
16. 如图,折叠矩形的一边 ,使点 落在 边的点 处,已知AB=8cm,BC=10cm,求 的长
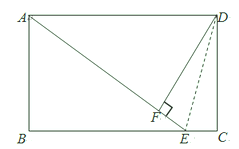
 17. 如果三角形有一边上的中线恰好等于这边的长,那么我们称这个三角形为“美丽三角形”.在Rt△ABC中,∠C=90°,AC ,若△ABC是“美丽三角形”,求BC的长.18. 如图,在长方形ABCD中,DC=6cm,在DC上存在一点E,沿直线AE把△ADE折叠,使点D恰好落在BC边上的点F处,若△ABF的面积为24cm2 , 那么折叠的△ADE的面积为多少?
17. 如果三角形有一边上的中线恰好等于这边的长,那么我们称这个三角形为“美丽三角形”.在Rt△ABC中,∠C=90°,AC ,若△ABC是“美丽三角形”,求BC的长.18. 如图,在长方形ABCD中,DC=6cm,在DC上存在一点E,沿直线AE把△ADE折叠,使点D恰好落在BC边上的点F处,若△ABF的面积为24cm2 , 那么折叠的△ADE的面积为多少?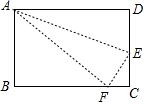 19. 如图,在 中, ,且周长为 ,点 从点 开始沿 边向 点以每秒 的速度移动;点 从点 开始沿 边向点 以每秒 的速度移动,如果 , 同时出发,问过 时, 的面积为多少?
19. 如图,在 中, ,且周长为 ,点 从点 开始沿 边向 点以每秒 的速度移动;点 从点 开始沿 边向点 以每秒 的速度移动,如果 , 同时出发,问过 时, 的面积为多少? 20. 如图,AD=8,CD=6,∠ADC=90°,AB=26,BC=24,求该图形的面积.
20. 如图,AD=8,CD=6,∠ADC=90°,AB=26,BC=24,求该图形的面积.


