（北师大版）2022-2023学年度第一学期八年级数学1.3 勾股定理的应用 同步测试
试卷更新日期：2022-07-10 类型：同步测试
一、单选题
-
1. 如图所示，甲渔船以8海里/时的速度离开港口O向东北方向航行，乙渔船以6海里/时的速度离开港口O向西北方向航行，他们同时出发，一个半小时后，甲、乙两渔船相距（ ）
A、12海里 B、13海里 C、14海里 D、15海里2. 梯子的底端离建筑物6米，10米长的梯子可以到达建筑物的高度是（ ）A、6米 B、7米 C、8米 D、9米3. 一个长方形抽屉长 ，宽 ，贴抽屉底面放一根木棒，那么这根木棒最长（不计木棒粗细）可以是（ ）A、 B、 C、 D、4. 《九章算术》是我国古代数学的经典著作，书中有一个“折竹抵地”问题：“今有竹高丈，末折抵地，问折者高几何？”意思是：一根竹子，原来高一丈（一丈为十尺），虫伤有病，一阵风将竹子折断，其竹梢恰好抵地，抵地处离原竹子根部三尺远，问：原处还有多高的竹子？（ ）
A、4尺 B、4.55尺 C、5尺 D、5.55尺5. 如图所示，小明准备测量一段河水的深度，他把一根竹竿竖直插到离岸边1.5m远的水底，竹竿高出水面0.5m，把竹竿的顶端拉向岸边，竿顶和岸边的水面刚好相齐，则河水的深度为（ ）
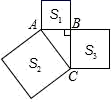
A、2m B、2.25m C、2.5m D、3m6. 由于台风的影响，一棵树在离地面6m处折断，树顶落在离树干底部8m处，则这棵树在折断前（不包括树根）长度是（ ）
A、8m B、10m C、16m D、18m7. 勾股定理是人类最伟大的科学发明之一．如图1，以直角三角形ABC的各边为边分别向外作正方形，再把较小的两张正方形纸片按图2的方式放置在最大的正方形内，三个阴影部分面积分别记为S1 ， S2 ， S3 ， 若已知S1＝2，S2＝5，S3＝8，则两个较小正方形纸片的重叠部分（四边形DEFG）的面积为（ ）
A、7 B、10 C、13 D、158. 如图①所示，有一个由传感器A控制的灯，要装在门上方离地高4.5 m的墙上，任何东西只要移至该灯5 m及5 m以内时，灯就会自动发光.请问一个身高1.5 m的学生要走到离墙多远的地方灯刚好发光？( )
A、4米 B、3米 C、5米 D、7米9. 如图所示，一场暴雨过后，垂直于地面的一棵树在距地面 处折断，树尖 恰好碰到地面，经测量 ，则树高为（ ）．
A、 B、 C、 D、10. 《九章算术》中的“折竹抵地”问题：今有竹高一丈，末折抵地，去根六尺．问折高者几何？意思是：一根竹子，原高一丈（一丈＝10尺），一阵风将竹子折断，其竹梢恰好抵地，抵地处离竹子底部6尺远，问折断处离地面的高度是多少？设折断处离地面的高度为 尺，则可列方程为（ ）A、 B、 C、 D、二、填空题
-
11. 如图，已知△ABC 中，∠ABC＝90°，以△ABC的各边为边，在△ABC外作三个正方形，S1 ， S2 ， S3分别表示这三个正方形的面积，若S1＝81，S2＝225，则BC＝ ．
12. 已知△ABC中，AB＝17，AC＝10，BC边上的高AD＝8．则边BC的长为 ．13. 如图，公路AC、BC互相垂直，公路AB的中点M与点C被湖隔开，若测得 ， ，则M，C两点间的距离为km.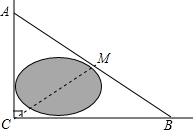
14. 如图，学校有一块长方形花铺，有极少数人为了避开拐角走“捷径”，在花铺内走出了一条“路”.他们仅仅少走了步路(假设2步为1米)，却踩伤了花草.
15. 在Rt△ABC中，∠C＝90°，∠A、∠B、∠C的对边分别为a、b、c，若a：b＝3：4，c＝20cm，则b＝ ．三、解答题
-
16. 如图是一面长方形彩旗完全展平时的尺寸图（单位：cm）．其中长方形ABCD是由双层白布缝制的穿旗杆用的旗裤，阴影部分DCEF为长方形绸缎旗面，将穿好彩旗的旗杆垂直插在操场上，旗杆从旗顶到地面的高度为220cm.在无风的天气里，彩旗自然下垂．求彩旗下垂时最低处离地面的最小高度h.
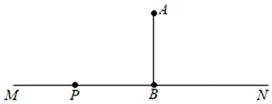
17. 在一棵树的10米高处 有两只猴子，其中一只猴子爬下树走到离树20米的池塘 ，另一只猴子爬到树顶 后直接跃向池塘的 处，如果两只猴子所经过距离相等，试问这棵树有多高．
18. 我方侦查员小王在距离东西向公路400米处侦查，发现一辆敌方汽车在公路上疾驶．他赶紧拿出红外线测距仪，测得汽车与他相距400米，10秒后，汽车与他相距500米，你能帮小王计算敌方汽车的速度吗？
19. 如图第4号台风“黑格比”的中心于2020年8月5日下午位于浙江省绍兴市境内的B处，最大风力有9级（23m/s），中心最低气压为990百帕，台风中心沿东北（BC）方向以25km/h的速度向D移动在距离B地250km的正北方有一A地，已知A地到BC的距离AD＝70km，那么台风中心经过多长时间从B点移到D点？如果在距台风中心70km的圆形区域内都将有受到台风破坏的危险，正在D点休闲的游人在接到台风警报后的几个小时内撤离才可脱离危险？
20. 小明爸爸给小明出了一道题：如图，修公路 遇到一座山，于是要修一条隧道 ．已知A ， B ， C在同一条直线上，为了在小山的两侧B ， C同时施工，过点B作一直线m（在山的旁边经过），过点C作一直线l与m相交于D点，经测量 ， ， 米， 米．若施工队每天挖100米，求施工队几天能挖完？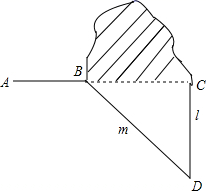
21. 为了积极宣传防疫，某区政府采用了移动车进行广播，如图，小明家在南大街这条笔直的公路 的一侧点A处，小明家到公路 的距离 为 米，假使广播车P周围 米以内能听到广播宣传，广播车P以 米/分的速度在公路 上沿 方向行驶时，假如小明此时在家，他是否能听到广播宣传？若能，请求出他总共能斪到多长时间的广播宣传？若不能，请说明理由.
